ahp层次分析法是啥

Posted 2023-04-19

AHP层次分析法是一种解决多目标复杂问题的定性和定量相结合进行计算决策权重的研究方法。

完整的AHP层次分析法通常包括四个步骤：

第一步：标度确定和构造判断矩阵；

此步骤即为原始数据（判断矩阵）的来源，比如本例中使用1-5分标度法（最低为1分，最高为5分）；并且结合出专家打分最终得到判断矩阵表格。

第二步：特征向量，特征根计算和权重计算；

此步骤目的在于计算出权重值，如果需要计算权重，则需要首先计算特征向量值，因此SPSSAU会提供特征向量指标。 同时得到最大特征根值（CI），用于下一步的一致性检验使用。

第三步：一致性检验分析；

在构建判断矩阵时，有可能会出现逻辑性错误，比如A比B重要，B比C重要，但却又出现C比A重要。因此需要使用一致性检验是否出现问题，一致性检验使用CR值进行分析，CR值小于0.1则说明通过一致性检验，反之则说明没有通过一致性检验。

针对CR的计算上，CR=CI/RI，CI值在求特征向量时已经得到，RI值则直接查表得出。

如果数据没有通过一致性检验，此时需要检查是否存在逻辑问题等，重新录入判断矩阵进行分析。

第四步：分析结论。

如果已经计算出权重，并且判断矩阵满足一致性检验，最终则可以下结论继续进一步分析。

详细参考：AHP层次分析法-SPSSAU

参考技术A 层次分析法（Analytic Hierarchy Process简称AHP）是将决策总是有关的元素分解成目标、准则、方案等层次，在此基础之上进行定性和定量分析的决策方法。该方法是美国运筹学家匹茨堡大学教授萨蒂于本世纪70年代初，在为美国国防部研究"根据各个工业部门对国家福利的贡献大小而进行电力分配"课题时，应用网络系统理论和多目标综合评价方法，提出的一种层次权重决策分析方法。
[编辑本段]层次分析法定义
所谓层次分析法，是指将一个复杂的多目标决策问题作为一个系统，将目标分解为多个目标或准则，进而分解为多指标（或准则、约束）的若干层次，通过定性指标模糊量化方法算出层次单排序（权数）和总排序，以作为目标（多指标）、多方案优化决策的系统方法，称为层次分析法。 层次分析法是将决策问题按总目标、各层子目标、评价准则直至具体的备投方案的顺序分解为不同的层次结构，然后得用求解判断矩阵特征向量的办法，求得每一层次的各元素对上一层次某元素的优先权重，最后再加权和的方法递阶归并各备择方案对总目标的最终权重，此最终权重最大者即为最优方案。这里所谓“优先权重”是一种相对的量度，它表明各备择方案在某一特点的评价准则或子目标，标下优越程度的相对量度，以及各子目标对上一层目标而言重要程度的相对量度。层次分析法比较适合于具有分层交错评价指标的目标系统，而且目标值又难于定量描述的决策问题。其用法是构造判断矩阵，求出其最大特征值。及其所对应的特征向量W，归一化后，即为某一层次指标对于上一层次某相关指标的相对重要性权值。

参考资料：http://baike.baidu.com/view/364279.html?wtp=tt#2

数学建模之层次分析法（AHP）

本文参考老师课上的PPT

层次分析法（AHP）,是一种解决多目标的复杂问题的定性与定量相结合的决策分析方法。由于其系统灵活简洁的优点，迅速地在我国社会经济各个领域内，如工程计划、资源规划、政策指定等，得到了广泛的重视和应用。

层次分析法大体可以分为四个步骤：
1.建立层次结构模型
2.构建判断（成对比较）矩阵
3.一致性检验

**1.建立结构模型。**需要将决策的目标、考虑的因素（决策准则）和决策对象按它们之间的相互关系分为最高层、中间层和最低层，绘出层次结构图。

2.构建判断（成对比较）矩阵。
构建原则有以下两点
1）不把所有因素放在一起比较，而是两两相互比较。
2）对此时采用相对尺度，以尽可能减少性质不同的诸因素相互比较的困难，以提高准确度。

判断矩阵元素aij的标度方法：

3.一致性检验。

其中lamda为判断矩阵的最大特征值，n为判断矩阵的阶数。由于不一致情况一般都会出现，因此，为了衡量CI的大小是否合理，因此引入随机一致性指标RI。

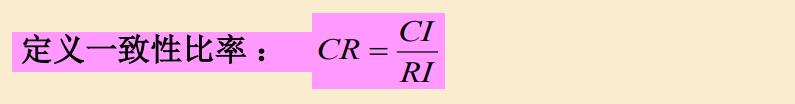
因此当算出CI之后，可通过判断矩阵阶数查表得RI计算出CR，如果CR<0.1则通过一致性检验。

matlab代码如下：

clc,clear
data = [1 1/2 4 3 3
    2 1 7 5 5
    1/4 1/7 1 1/2 1/3
    1/3 1/5 2 1 1
    1/3 1/5 3 1 1];%需要检验的一致性矩阵
[n,m]=size(data);

%求特征值特征向量,找到最大特征值对应的特征向量
[V,D]=eig(data);%求矩阵的特征值和特征向量，V为特征向量矩阵，D为特征值矩阵。
lenda=max(D);
lendada=max(lenda);%求对角线向量
col = find(D(1,:) == max(lenda));%求最大特征值
lenda_V = V(:, col);% 最大特征值的特征向量，能够用于计算特征权重
for i = 1:n
    w(i,1) = lenda_V(i,1)/sum(lenda_V);
end

%一致性检验
CI=(lendada-n)/(n-1);
RI=[0,0,0.58,0.9,1.12,1.24,1.32,1.41,1.45,1.49,1.52,1.54,1.56,1.58,1.59];
%判断是否通过一致性检验
CR=CI/RI(n);
if CR>=0.1
   fprintf('没有通过一致性检验\\n');
else
  w
  fprintf('通过一致性检验\\n');
end