应用统计学描述数据的离散程度

Posted 2022-12-04 古月书斋

一、极差

极差又称全距(Range)，以R表示，用来表示统计数据中的最大值与最小值之间的差距，即最大值减最小值后所得之数据。

二、四分位差

四分位差是上四分位数（Q3，即位于75%）与下四分位数（Q1，即位于25%）的差。

四分位差可以用来评判中位数的好坏。如果四分位差越小，中位数就越有代表性。

三、平均差

平均差是各数据同其均值的离差绝对值的算术平均数。

 四、平标准差与方差

未分组公式

分组公式

 数学性质

 

 

 

 是否标志的方差与标准差

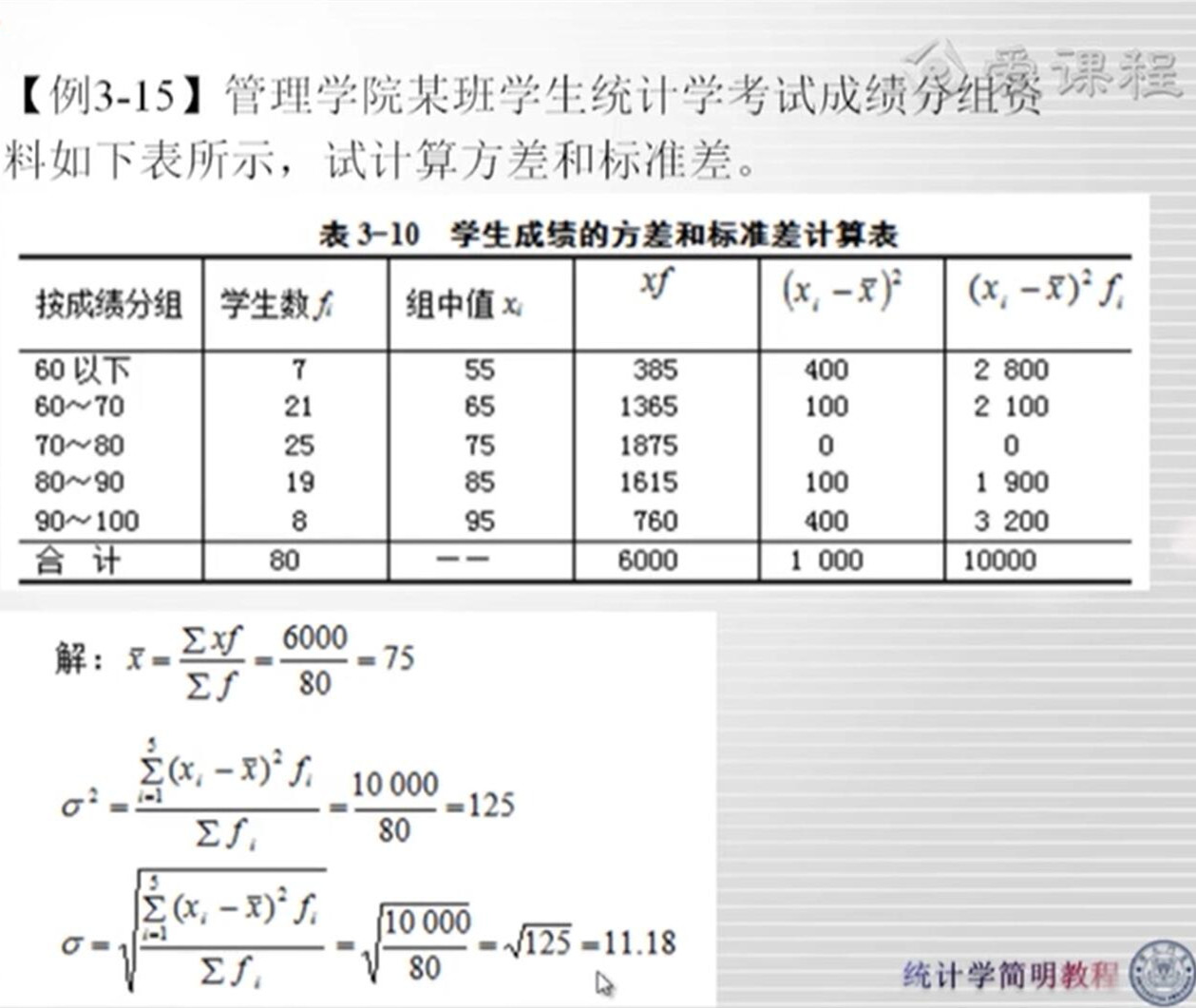
总体方差和样本方差

方差分为总体方差和样本方差。如何计算方差说着很简单，但你知道这里的均数是指什么均数吗？答案是“总体均数”，对，是“总体均数”！也就是说，如果总体均数已知，你求样本方差的时候是直接除以n，计算公式如下：

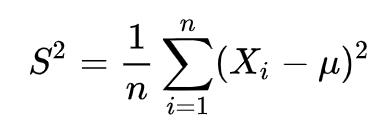
但是，现实生活中，我们往往不清楚一个总体的总体均数，而是通过抽取样本，计算样本均数，然后用样本均数来代替总体均数。这时样本方差的计算就变为：

通过数学公式推到，可以找到如下定量关系：

 

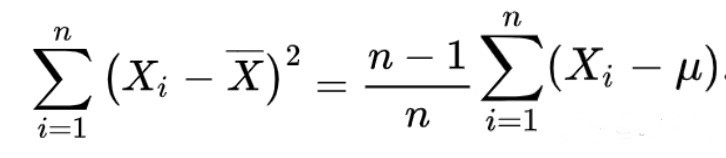
把上式稍作调整，我们便可以得到：

 

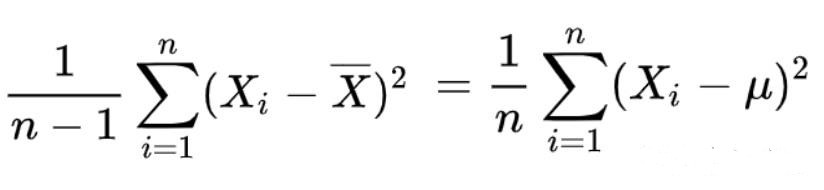
仔细看看，上面左右等式就是我们开篇提出的样本方差的计算方法。右边是是减去的总体均数，即理想情况下，知道总体均数的计算方法；它等于左边运用样本均数的求法，就是这么神奇！由此，样本均数之所以要除以（n-1）实际上是通过数学公式推导出来的，而不是拍脑袋决定的。而引入自由度的概念，某种程度是为数学推导的结论增添了实际含义。

五、变异系数

 六、异众比例

 异众比率主要用于定类变量，比如颜色。