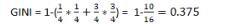☀️数据挖掘期末复习汇总（再也不用熬夜复习了）

Posted 2022-12-03 °PJ想做前端攻城狮

填空题

欧几里得距离（欧氏距离）

例题：测试样本，属性为：[1,0,2]，训练样本，属性为：[2,0,2]，求测试样本到训练样本的欧氏距离。

答案：1

公式参考

余弦相似度

例题：x=[3,2,0,5,0,0,0,2,0,0],y=[1,0,0,0,0,0,0,1,0,2],求两者之间的夹角余弦相似度

答案：0.31

公式参考

---

简单匹配系数

例题：x=[0,1,1,0,0],y=[1,1,0,0,1],求两者之间的简单匹配系数

答案：0.4

公式参考

Jaccard系数

例题：x=[0,1,1,0,0],y=[1,1,0,0,1],求两者之间的Jaccard相似性系数

答案：0.25

公式参考

---

数据集的Classification Error

例题：已知一个数据集，其中有3个类的样本，这3个类的样本数量分别为1、1、3，求Classification Error

答案： 0.4

解答

公式参考

数据集的GINI（基尼系数）

例题：已知一个数据集，其中有2个类的样本，这2个类的样本数量分别为1、3，求该数据集的GINI。

答案： 0.375

解答：

参考公式

---

召回率

例题：TP=90，FN=20，TN=120，FP=10，计算其召回率

答案： 9/11

公式参考

精度

例题：TP=90，FN=20，TN=120，FP=10，求计算其精度

答案： 9/10

公式

---

问答题

简述支持向量机的“最大边缘”原理

即追求分类器的泛化能力最大化。即希望所找到的决策边界，在满足将两类数据点正确的分开的前提下，对应的分类器边缘最大。这样可以使得新的测试数据被错分的几率尽可能小。

简述软边缘支持向量机的基本工作原理

对存在数据污染、近似线性分类的情况，可能并不存在一个最优的线性决策超平面；当存在噪声数据时，为保证所有训练数据的准确分类，可能会导致过拟合。因此，需要允许有一定程度“错分”，又有较大分界区域的最优决策超平面，即软间隔支持向量机。
软间隔支持向量机通过引入松弛变量、惩罚因子，在一定程度上允许错误分类样本，以增大间隔距离。在分类准确性与泛化能力上寻求一个平衡点。

简述非线性支持向量机的基本工作原理

对非线性可分的问题，可以利用核变换，把原样本映射到某个高维特征空间，使得原本在低维特征空间中非线性可分的样本，在新的高维特征空间中变得线性可分，并使用线性支持向量机进行分类。

---

计算题

朴素贝叶斯分类

问题

1. 已知训练数据集如上图：该数据集中，求P(yes)， P(no)
2. 已知待分类的测试样本X=（有房=否，婚姻=已婚）

参考步骤

答案参考

---

ID3决策树，计算数据集的熵、期望和信息增益

熵公式参考

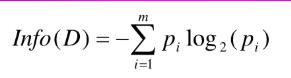
1. 求该数据集的熵为 Info(D)。

   P(yes)=0.6，P(no)= 0.4

   Info(D) = –(3/5)log2(3/5)–(2/5)log2(2/5)

2. 以Attribute1为分裂属性，将数据集分成三个子集D1、D2、D3，分别对应Attribute1=V1a，Attribute1=V1b，Attribute1=V1c。求这三个子集的熵

   计算三个子集的样本数量与原始数据集的比例

   D1:0.4 D2:0.2 D3:0.4

   求D1的熵。

   P(yes)=1/4，P(no)= 3/4

   Info(D1)=– (1/4)log2(1/4)–(3/4)log2(3/4)

   同理

   Info(D2) = – 1log2(1)

   Info(D3) = – (1/4)log2(1/4)–(3/4)log2(3/4)

---

期望信息公式参考

1. 以Attribute1为分裂属性，将数据集分成三个子集D1、D2、D3，分别对应Attribute1=V1a，Attribute1=V1b，Attribute1=V1c。求该划分的期望信息

   InfoA（D） = P(D1)xInfo(D1)+P(D1)xInfo(D1)+P(D1)xInfo(D1)

   InfoA (D) =

   提示：

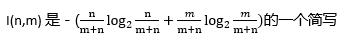
2. 在上题的基础上，求该划分的信息增益

   Gain（A）= Info（D）- InfoA（D）

   

   信息增益公式参考

   

   ---

欧氏距离和KNN分类

已知有5个训练样本，分别为：
样本1，属性为：[2,0,2] 类别 0
样本2，属性为：[1,5,2] 类别 1
样本3，属性为：[3,2,3] 类别 1
样本4，属性为：[3,0,2] 类别 0
样本5，属性为：[1,0,6] 类别 0

有1个测试样本，属性为：[1,0,2]

（1）测试样本到5个训练样本（样本1、2、3、4、5）的欧氏距离依次为：1、5、3、2、4

（2）K=3，距离测试样本最近的k个训练样本依次为：样本1、样本4、样本3

（3）距离最近的k个训练样本类别依次为：类别0、类别0、类别1

（4）KNN算法得到的测试样本的类别为： 类别0

注意：具体欧氏距离参考上面填空做法，KNN测试样本类别，选择K个中出现频率最高的。

---

求给定数据集的频繁K项集、指定关联规则的支持度及置信度

公式参考

例题

已知购物篮数据如下表所示，回答以下问题。

（1）计算所有2项集及其支持度。

Bread，Mike：s = 3/5
Bread，Diaper：s = 4/5
Bread，Beer：s = 2/5
Diaper，Mike：s = 4/5
Beer，Mike：s = 2/5
Diaper，Beer：s = 3/5

（2）给定最小支持度阈值为2/5，列出所有频繁2项集。

所有的S都大于等于最小支持度阈值
Bread，MikeBread，DiaperBread，BeerDiaper，MikeBeer，MikeDiaper，Beer

（3）关联规则X->Y的支持度计算公式是什么？

（4）关联规则X->Y的置信度计算公式是什么？

（5）计算规则Milk, Bread -> Diaper 的支持度和置信度。

即求Milk, Bread，Diaper 的支持度. 
其支持度计数为3，事务总数为5.
故支持度s(Milk, Bread，Diaper ) = 3/5.
Milk, Bread 的支持度计数为3.
所以Milk, Bread -> Diaper 的置信度c=3/3 = 1