ETCD中K8S的元数据

Posted 2023-04-18

参考技术A 假设你已经通过kubeadm 安装好了K8S 和对应的etcd集群

Kubenretes1.6中使用etcd V3版本的API，使用etcdctl直接ls的话只能看到/kube-centos一个路径。需要在命令前加上ETCDCTL_API=3这个环境变量才能看到kuberentes在etcd中保存的数据。

如果是使用 kubeadm 创建的集群，在 Kubenretes 1.11 中，etcd 默认使用 tls ，这时你可以在 master 节点上使用以下命令来访问 etcd ：

-w指定输出格式
将得到这样的json的结果：

使用--prefix可以看到所有的子目录，如查看集群中的namespace：

输出结果中可以看到所有的namespace。

key的值是经过base64编码，需要解码后才能看到实际值，如：

etcd中kubernetes的元数据
我们使用kubectl命令获取的kubernetes的对象状态实际上是保存在etcd中的，使用下面的脚本可以获取etcd中的所有kubernetes对象的key：

注意，我们使用了ETCD v3版本的客户端命令来访问etcd。

通过输出的结果我们可以看到kubernetes的原数据是按何种结构包括在kuberentes中的，输出结果如下所示：

我们可以看到所有的Kuberentes的所有元数据都保存在/registry目录下，下一层就是API对象类型（复数形式），再下一层是namespace，最后一层是对象的名字。

以下是etcd中存储的kubernetes所有的元数据类型：

转自

Python 详解K-S检验与3σ原则剔除异常值

文章目录

• 一、引言
• 二、3σ原则
• 三、K-S检验
• 四、Python实现

---

一、引言

异常值分析是检验数据是否有录入错误，是否含有不合常理的数据。忽视异常值的存在是十分危险的，不加剔除地将异常值放入数据的计算分析过程中，会对结果造成不良影响；重视异常值的出现，分析其产生的原因，经常成为发现问题进而改进决策的契机。

异常值是指样本中的个别值，其数值明显偏离其他的观测值。异常值也称为离群点，异常值分析也称为离群点分析。

而对于数据异常值的处理，3σ 原则是一种基于统计的方法，简单实用。

---

二、3σ原则

什么叫 3σ 原则呢？

• 3σ 原则，又叫拉依达原则，它是指假设一组检测数据中只含有随机误差，需要对其进行计算得到标准偏差，按一定概率确定一个区间，对于超过这个区间的误差，就不属于随机误差而是粗大误差，需要将含有该误差的数据进行剔除。
• 局限性：仅局限于对正态或近似正态分布的样本数据处理，它是以测量次数充分大为前提（样本>10），当测量次数少的情形用准则剔除粗大误差是不够可靠的。在测量次数较少的情况下，最好不要选用该准则。

3σ 原则：

• 数值分布在（μ-σ，μ+σ）中的概率为 0.6827
• 数值分布在（μ-2σ，μ+2σ）中的概率为 0.9545
• 数值分布在（μ-3σ，μ+3σ）中的概率为 0.9973

其中，μ 为平均值，σ 为标准差。一般可以认为，数据 Y 的取值几乎全部集中在（μ-3σ，μ+3σ)区间内，超出这个范围的可能性仅占不到 0.3%，这些超出该范围的数据可以认为是异常值。

在实验科学中有对应正态分布的 3σ 定律（Three-sigma Law），是一个简单的推论，内容是 “几乎所有” 的值都在平均值正负三个标准差的范围内，也就是在实验上可以将 99.7% 的机率视为 “几乎一定” 。不过上述推论是否有效，会视探讨领域中 “显著” 的定义而定，在不同领域，“显著” 的定义也随着不同，例如在社会科学中，若置信区间是在正负二个标准差（95%）的范围，即可视为显著。但是在粒子物理中，若是发现新的粒子，置信区间要到正负五个标准差（99.99994%）的程度。

即使在不是正态分布的情形下，也有另一个对应的 3σ 定律（three-sigma rule）。即使是在非正态分布的情形下，至少会有 88.8% 的机率会在正负三个标准差的范围内，这是依照切比雪夫不等式的结果。若是单模分布（unimodal distributions）下，正负三个标准差内的机率至少有95%，若符合特定一些条件的分布，机率可能会到 98% 。所以如果数据不服从正态分布，也可以用远离平均值的标准差的自定义倍数来描述。

---

三、K-S检验

可以使用 K-S 检验一列数据是否服从正态分布

from scipy.stats import kstest

kstest(rvs, cdf, args=(), N=20, alternative='two-sided', mode='auto')
https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.kstest.html

补充学习：

• 知乎 | 非参数统计之分布检验[1]:Kolmogorov-Smirnov检验
• 博客园 | 柯尔莫可洛夫-斯米洛夫检验（Kolmogorov–Smirnov test，K-S test）

---

四、Python实现

Python实现步骤具体步骤如下：

• 首先需要保证数据列大致上服从正态分布（可以使用 box-cox 变换等）；
• 计算需要检验的数据列的平均值 μ 和标准差 σ；
• 比较数据列的每个值与平均值的偏差是否超过 3 倍标准差，如果超过 3 倍，则为异常值；
• 剔除异常值，得到规范的数据。

K-S 正态分布检验和 3σ 原则剔除异常值，Python 代码如下：

import numpy as np
import pandas as pd
from scipy.stats import kstest
from scipy.special import boxcox1p
from scipy.stats import boxcox_normmax
from scipy.special import inv_boxcox


def KsNormDetect(df):
    # 计算均值
    u = df['value'].mean()
    # 计算标准差
    std = df['value'].std()
    # 计算P值
    print(kstest(df['value'], 'norm', (u, std)))
    res = kstest(df['value'], 'norm', (u, std))[1]
    print('均值为：%.2f，标准差为：%.2f' % (u, std))
    # 判断p值是否服从正态分布，p<=0.05 拒绝原假设 不服从正态分布
    if res <= 0.05:
        print('该列数据不服从正态分布')
        print("-" * 66)
        return True
    else:
        print('该列数据服从正态分布')
        return False


def OutlierDetection(df, ks_res):
    # 计算均值
    u = df['value'].mean()
    # 计算标准差
    std = df['value'].std()
    if ks_res:
        # 定义3σ法则识别异常值
        outliers = df[np.abs(df['value'] - u) > 3 * std]
        # 剔除异常值，保留正常的数据
        clean_data = df[np.abs(df['value'] - u) < 3 * std]
        # 返回异常值和剔除异常值后的数据
        return outliers, clean_data

    else:
        print('请先检测数据是否服从正态分布')
        return None


if __name__ == '__main__':
    # 构造数据  某一列数据  含有异常值
    data = np.random.normal(60, 5, 200)
    data[6], data[66], data[196] = 16, 360, 180
    print(data)
    
    print("-" * 66)
    # 可以转换为pandas的DataFrame 便于调用方法计算均值和标准差
    df = pd.DataFrame(data, columns=['value'])
    # box-cox变换
    lam = boxcox_normmax(df["value"] + 1)
    df["value"] = boxcox1p(df['value'], lam)
    # K-S检验
    ks_res = KsNormDetect(df)
    outliers, clean_data = OutlierDetection(df, ks_res)
    # 异常值和剔除异常值后的数据
    outliers = inv_boxcox(outliers, lam) - 1
    clean_data = inv_boxcox(clean_data, lam) - 1
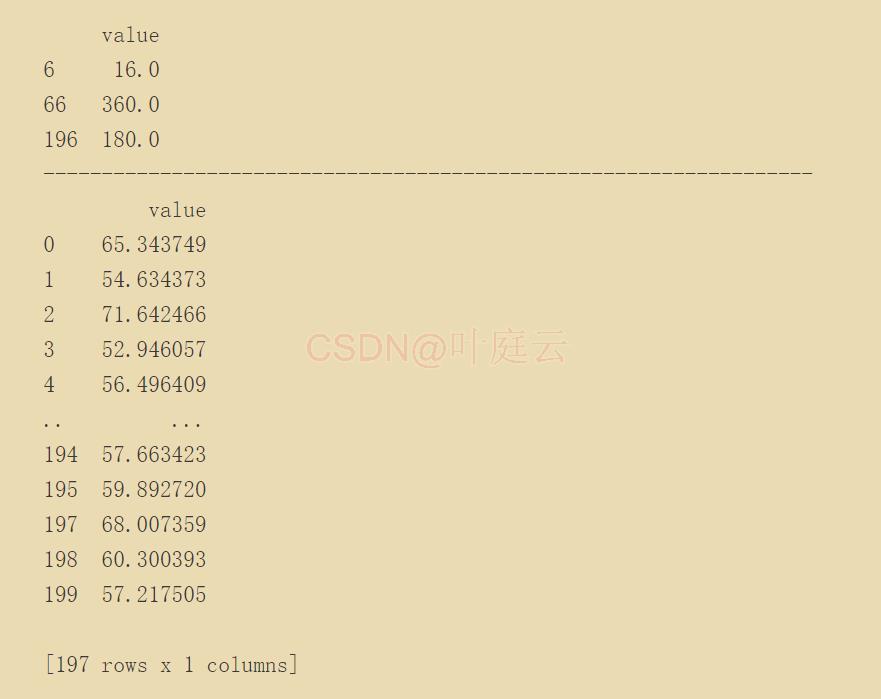
    print(outliers)
    print("-" * 66)
    print(clean_data)

剔除异常值结果如下：

---

补充学习：

• Python 机器学习 | 正态分布检验以及异常值处理3σ原则
• Python实现基于3σ原则的异常值检测
• 知乎 | 机器学习中的异常值检测
• 公众号文章 | 什么是脏数据？怎样用箱形图分析异常值？终于有人讲明白了