matlab代码实现四阶龙格库塔求解微分方程

Posted 2022-12-03 studyer_domi

前言

数值分析中，龙格－库塔法（Runge-Kutta methods）是用于非线性常微分方程的解的重要的一类隐式或显式迭代法。这些技术由数学家卡尔·龙格和马丁·威尔海姆·库塔于1900年左右发明。

龙格-库塔(Runge-Kutta)方法是一种在工程上应用广泛的高精度单步算法，其中包括著名的欧拉法，用于数值求解微分方程。由于此算法精度高，采取措施对误差进行抑制，所以其实现原理也较复杂。

在各种龙格－库塔法当中有一个方法十分常用，以至于经常被称为“RK4”或者就是“龙格－库塔法”。该方法主要是在已知方程导数和初值信息，利用计算机仿真时应用，省去求解微分方程的复杂过程。

令初值问题表述如下。

则，对于该问题的RK4由如下方程给出：

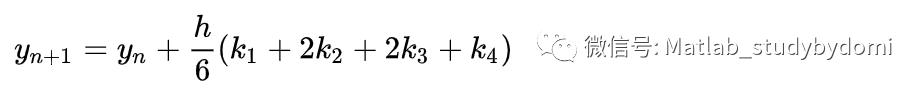
其中

这样，下一个值（yn+1）由现在的值（yn）加上时间间隔（h）和一个估算的斜率的乘积所决定。该斜率是以下斜率的加权平均：

k1是时间段开始时的斜率；

k2是时间段中点的斜率，通过欧拉法采用斜率k1来决定y在点tn+h/2的值；

k3也是中点的斜率，但是这次采用斜率k2决定y值；

k4是时间段终点的斜率，其y值用k3决定。

当四个斜率取平均时，中点的斜率有更大的权值：

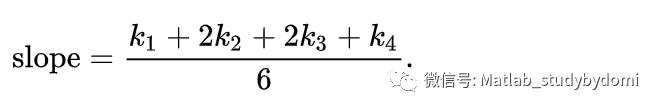
RK4法是四阶方法，也就是说每步的误差是h阶，而总积累误差为h阶。

注意上述公式对于标量或者向量函数（y可以是向量）都适用。

matlab代码实现

问题：dy/dt=y-t^2+1 ; 0<=t<=2 ; y(0)=0.5;

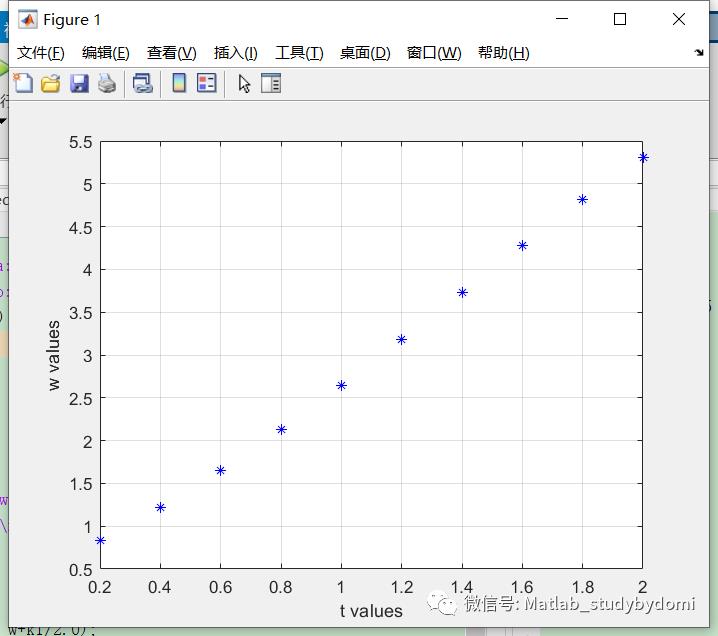
clearclcclose all
f = @(t,y) (y-t^2+1);
a = input('开始时间, a:  ');b = input('结束时间, b:  ');n = input('步数, n: ');  % n=(b-a)/halpha = input('初始值, alpha:  ');
h = (b-a)/n;
t = a;w = alpha;fprintf('  t         w\\n');fprintf('%5.3f %11.7f\\n', t, w);
for i = 1:n    k1 = h*f(t,w);    k2 = h*f(t+h/2.0, w+k1/2.0);    k3 = h*f(t+h/2.0, w+k2/2.0);    k4 = h*f(t+h,w+k3);    w = w+(k1+2.0*(k2+k3)+k4)/6.0;    t = a+i*h;
    fprintf('%5.3f %11.7f\\n', t, w);    plot(t,w,'b*'); grid on;    xlabel('t values'); ylabel('w values');    hold on;end

开始时间, a:  0结束时间, b:  2步数, n: 10初始值, alpha:  0.5  t         w0.000   0.50000000.200   0.82929330.400   1.21407620.600   1.64892200.800   2.12720271.000   2.64082271.200   3.17989421.400   3.73234011.600   4.28340951.800   4.81508572.000   5.3053630