matlab实现RK45（Runge-Kutta45ode45）求解器算法

Posted 2022-12-03 studyer_domi

RK45求解器，又称为Dormand-Prince求解器。这是比较精确的求解器，可以快速地求解微分方程，但是，需要消耗一些内存。在matlab simulink中默认条件下，系统自动选择RK45求解器。用户可以根据实际问题，选择合适的求解器。

Dopri54是Dormand / Prince龙格-库塔的一种方法，Dopri54由龙格-库塔简单法构成，阶为5和4。因此，五阶龙格-库塔法是利用一步向前+四阶龙格-库塔法估计误差。

本文分享一个简单例子来从m代码实现RK45求解器，matlab也可以用自带的ode45函数来求解微分方程:Matlab通过ode系列函数求解微分方程

假定y'=y，y(0) = 1，很明显结果的理论解为y(t)=e^t，

matlab代码

clcclose allcleary0 = 1;[t,y] = dopri54c('fun', 0, 1, y0, 0.0001);
figureplot(t,y)

function u = fun(x, y)u=y;

% funcion - 函数句柄% t0 - 开始时间.% t1 - 结束时间.% y0 - 初始值.% tol - 局部误差% OUTPUT% y - 输出t=t0;y=y0;h=tol^(1/5)/4;step=0;nrej=0;fcall=1;a4=[44/45 -56/15 32/9]';a5=[19372/6561 -25360/2187 64448/6561 -212/729]';a6=[9017/3168 -355/33 46732/5247 49/176 -5103/18656]';a7=[35/384 0 500/1113 125/192 -2187/6784 11/84]';e=[71/57600 -1/40 -71/16695 71/1920 -17253/339200 22/525]';k1=feval(funcion,t,y);t_1 = t;y_1 = y;
while t < t1    if t+h > t1        h=t1-t;     end    k2=feval(funcion,t+h/5,y+h*k1/5);    k3=feval(funcion,t+3*h/10,y+h*(3*k1+9*k2)/40);    k4=feval(funcion,t+4*h/5,y+h*(a4(1)*k1+a4(2)*k2+a4(3)*k3));    k5=feval(funcion,t+8*h/9,y+h*(a5(1)*k1+a5(2)*k2+a5(3)*k3+a5(4)*k4));    k6=feval(funcion,t+h,y+h*(a6(1)*k1+a6(2)*k2+a6(3)*k3+a6(4)*k4+a6(5)*k5));    yt=y+h*(a7(1)*k1+a7(3)*k3+a7(4)*k4+a7(5)*k5+a7(6)*k6);    k2=feval(funcion,t+h,yt);    est=norm(h*(e(1)*k1+e(2)*k2+e(3)*k3+e(4)*k4+e(5)*k5+e(6)*k6),inf);    fcall=fcall+6;
    if est < tol        t=t+h;        k1=k2;        step=step+1;        y=yt;        t_1 = [t_1; t];        y_1 = [y_1; y];    else        nrej=nrej+1;    end    h=.9*min((tol/(est+eps))^(1/5),10)*h;
end

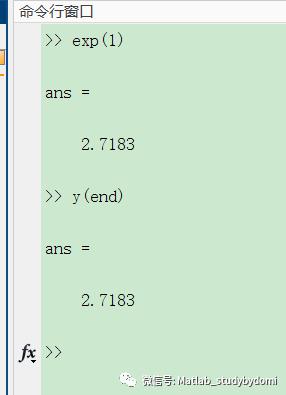
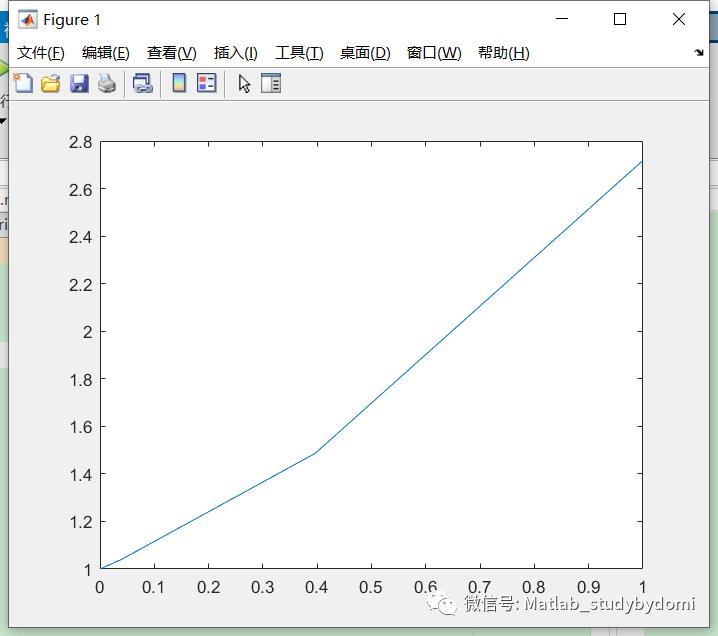
结果符合预期