鲸鱼优化算法WOA求解旅行商TSP优化问题（2022.6.2）

Posted 2023-02-19 jing_zhong

鲸鱼优化算法WOA求解旅行商TSP优化问题（2022.6.2）

• 引言
• 1、鲸鱼优化算法WOA
• • 1.1 WOA算法原理介绍
  • • 1.1.1 包围猎物
    • 1.1.2 气泡网式攻击猎物（开发阶段）
    • 1.1.3 寻找猎物（探索阶段）
  • 1.2 WOA算法流程
  • 1.3 WOA官方源码
• 2、WOA源码测试运行（Matlab）
• • 2.1 WOA代码简介
  • • 2.1.1 Get_Functions_details.m
    • 2.1.2 func_plot.m
    • 2.1.3 initialization.m
    • 2.1.4 WOA.m
    • 2.1.5 main.m（运行文件）
  • 2.2 运行结果（函数F1~F23）
• 3、WOA求解TSP（C++ or Python)
• • 3.1 WOA求解TSP（C++）
  • • 3.1.1 C++代码（main.cpp）
    • 3.1.2 运行结果
  • 3.2 WOA求解TSP（Python）
  • • 3.2.1 Python代码（WOA.py)
    • 3.2.2 运行结果
• 4、总结

引言

        作为世界上最大的哺乳动物，一条成年鲸鱼的身长可达到30m，体重能达到180t。鲸鱼大多被认为是食肉动物，它们从不睡觉，因为必须从海洋表面呼吸。事实证明，鲸鱼可以像人类一样思考、学习、判断、交流，它们也被认为是具有情感的高智商动物。另一件有趣的事情是鲸鱼的社交行为：它们独居或群居，但大多是处于群体当中。成年座头鲸（Megaptera novaeangliae）几乎和校车一样大。它们最喜欢的猎物是磷虾和小鱼群。

1、鲸鱼优化算法WOA

WOA算法原始论文

Web of Science高被引论文

百度学术检索结果

        2016年，来自澳大利亚的两位研究人员Mirjalili Seyedali和Lewis Andrew通过模拟自然界生物座头鲸的社会行为，提出了一种元启发式的优化算法——鲸鱼优化算法WOA，撰写的论文在Advances in Engineering Software期刊上在线发表，被SCI收录，引起了学者们的广泛关注，迄今为止论文的被引频次高达3496。

座头鲸的气泡网法捕食行为示意图

        算法的核心在于座头鲸的气泡网式捕捉策略，算法利用三个操作算子来模拟座头鲸对猎物的搜索、包围猎物和气泡网觅食行为。经过29个数学优化问题和6个结构设计问题的实际测试，结果证明，与其他传统的元启发式算法相比，WOA具有十分明显的计算优势。(注：WOA算法源代码已公开，可点击下载)

1.1 WOA算法原理介绍

1.1.1 包围猎物

        座头鲸能够识别猎物位置并且对其进行转圈包围，WOA算法假设当前最优的候选位置就是目标猎物或者说更接近最优猎物的位置，在定义了最好的搜索智能体后，其他的搜索智能体就会向着最好的搜索智能体来尝试更新它们的位置，这个行为可以用下列方程来表示：
$$\vec{D}=|\vec{C}\cdot \overrightarrow{X^{\ast }}(t)-\vec{X}(t)|\text{\hspace{1em}(公式1)}$$$$\vec{X}(t+1)=\overrightarrow{X^{\ast }}(t)-\vec{A}\cdot \vec{D}\text{\hspace{1em}(公式2)}$$
        其中，$t$ 表示当前代数；$\vec{A}$ 和 $\vec{C}$ 是系数向量；$X^{\ast }$ 是目前为止所获取最优解的位置向量；$\vec{X}$是位置向量；$||$ 是绝对值；$\cdot$ 是点积，对应元素逐点相乘。
$$\vec{A}=2\vec{a}\cdot \vec{r}-\vec{a}\text{\hspace{1em}(公式3)}$$$$\vec{C}=2\cdot \vec{r}\text{\hspace{1em}(公式4)}$$
        $\vec{a}$ 随着代数的增加线性递减，取值范围为[2,1]；$\vec{r}$ 是一个取值范围在[0,1]的随机向量。

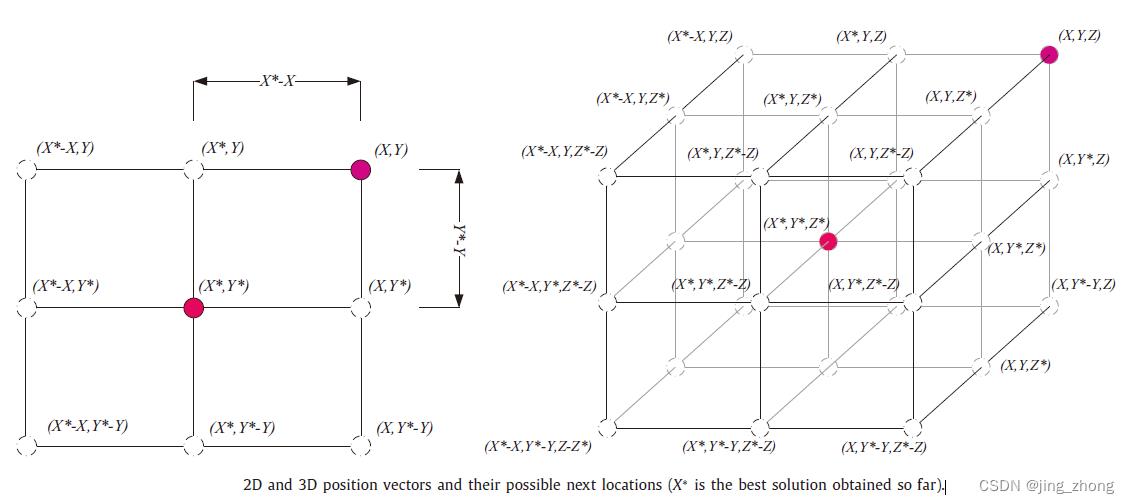
        如上图所示，无论是二维空间还是三维空间，通过对当前位置调整$\vec{A}$ 和 $\vec{C}$的值可到达最好个体周围的不同位置，因此，公式2可用来根据当前最优解的邻域对一些搜索个体的位置进行更新，这样来实现对猎物的包围。

1.1.2 气泡网式攻击猎物（开发阶段）

        为了对座头鲸的气泡网攻击猎物方法进行建模，故而设计了以下两种方法，如下图所示。

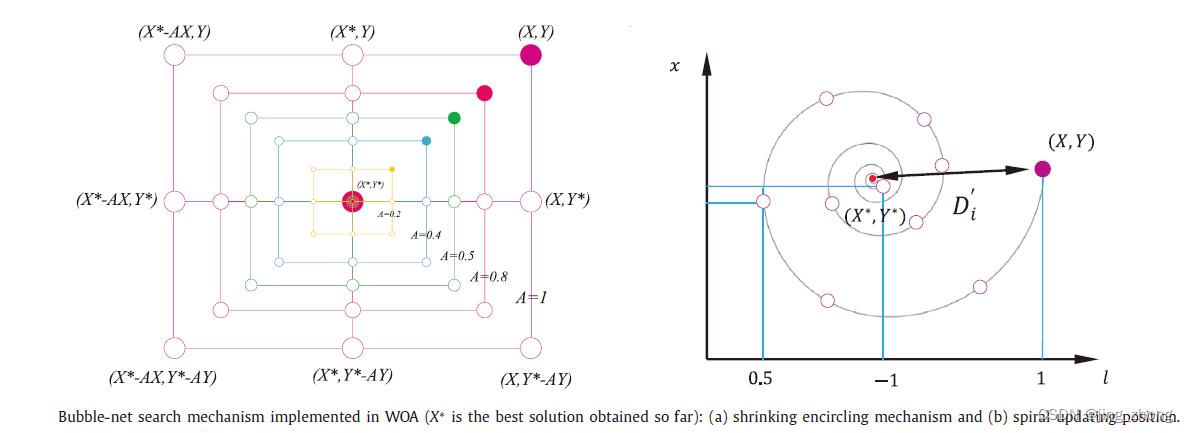
1. 收缩环绕机制：这个行为可通过减小公式3中 $\vec{a}$ 的值来实现，当a随着代数增加从2逐渐下降到0，$\vec{A}$的取值范围,为[-a,a]。如果设定 $\vec{A}$ 的随机值在[-1,1]，那么一个搜索个体的新位置就会位于其原来位置和当前最优个体位置之间。上图中（a）展示了2维空间 $0\le A\le 1$ 时从 $(X,Y)$ 向 $(X^{\ast },Y^{\ast })$ 的可能搜索位置。
2. 螺旋线更新位置：如上图中（b）所示，首先计算鲸鱼所在位置 $(X,Y)$到猎物所在位置$(X^{\ast },Y^{\ast })$的距离，然后在鲸鱼和猎物的位置之间建立一个螺旋方程来模拟座头鲸的螺旋形运动，如下所示： X ⃗ ( t + 1 ) = D ′ ⃗ ⋅ e b l ⋅ c o s ( 2 π l ) + X ∗ ⃗ ( t ) (公式5) \\vecX(t+1)=\\vecD^' \\cdot e^bl \\cdot cos(2\\pi l) + \\vecX^*(t) \\tag公式5 X (t+1)=D′ ⋅ebl⋅cos(2πl)+以上是关于鲸鱼优化算法WOA求解旅行商TSP优化问题（2022.6.2）的主要内容，如果未能解决你的问题，请参考以下文章

   MATLAB实战系列（二十九）-头脑风暴优化（BSO）算法求解旅行商问题（TSP）-交叉算子

   TSP基于matlab麻雀算法求解旅行商问题含Matlab源码 1575期

   matlab改进鲸鱼算法求解路径优化

   matlab改进鲸鱼算法求解路径优化

   matlab改进鲸鱼算法求解路径优化

   SSA TSP基于matlab麻雀算法求解旅行商问题含Matlab源码 1575期