编译原理词法分析

Posted 2022-12-02 jzyhywxz

上一篇文章我们介绍了在词法分析中涉及到的词法单元、模式和词素的概念，并给出了正则表达式的递归定义，以及如何把一个正则表达式转换成一个状态转换图。本篇文章将接着上一篇文章的内容，继续介绍词法分析的一个重要内容——有穷自动机。

有穷自动机

一个有穷自动机可以把一个描述词素的模式变成一个词法分析器，从本质上来讲，有穷自动机是与状态转换图相类似的图，它有以下特点：

• 有穷自动机是一个识别器，它只能对每个输入符号串简单的输出“yes”或“no”，表示是否能够识别此符号串；
• 有穷自动机和状态转换图类似，它具有有限个数的结点，每个结点表示一个状态，并且这些状态中有一个初始状态和若干个终止状态。从一个状态s开始，经过被某个符号a（可能包括ε）标记的有向边，可以到达另一个状态t或者回到状态s（成环）；
• 有穷自动机分为不确定的有穷自动机和确定的有穷自动机，不确定的和确定的有穷自动机能识别的语言集合是相同的。

不确定的有穷自动机

一个不确定的有穷自动机（Nondeterministic Finite Automate，下文简称NFA）由以下部分组成：

• 结点集合：一个有穷的状态集合S；
• 标记集合：一个输入符号集合∑，以及空串ε；
• 转换函数：它为每个状态和∑∪ε中的每个符号都给出了相应的后继状态的集合。即转换函数的输入是某个状态s和∑∪ε中的某个符号a，输出是从状态s出发，经过标记为a的边，能够到达的所有状态的集合；
• 初始状态：S的一个状态被指定为初始状态；
• 终止状态：S的一个子集被指定为终止状态的集合。

从NFA的组成部分可以看出，它和状态转换图的不同之处在于：

1. 同一个符号可以标记从同一个状态出发到达多个目标状态的多条边，即转换函数是一对多关系的；
2. 一条边的标号不仅可以是输入符号集合中的符号，也可以是空串ε。

另外，我们也可以把一个NFA用一张转换表来表示，表的每行对应状态，表的每列对应输入符号和ε（实际上就是在数据结构中学过的图的邻接表）。下面是一个NFA及其对应的转换表：

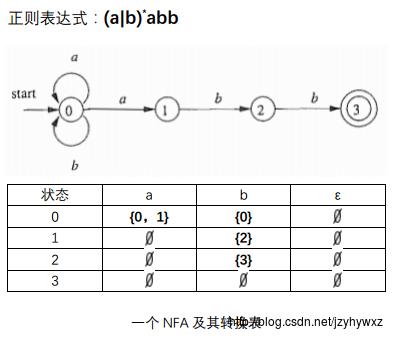
确定的有穷自动机

确定的有穷自动机（Deterministic Finite Automate，下文简称DFA）是NFA的一个特例，其中：

• 标记集合：一个输入符号集合∑，但不包含空串ε；
• 转换函数：对每个状态s和每个输入符号a，有且仅有一条标号为a的边离开s，即转换函数的对应关系从一对多变为了一对一。

同样的，一个DFA也能用一个转换表来表示。由于此时每个表项中只有一个状态，因此可以省去括号，下面是和在NFA中同一个正则表达式对应的DFA及其转换表：

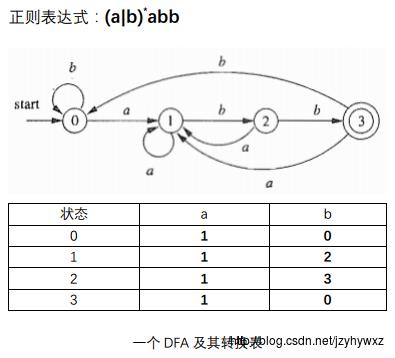
从NFA到DFA的转换

NFA抽象地表示了用来识别某个语言中的串的算法，而相应的DFA则是一个简单具体的识别串的算法。在构造词法分析器时，真正实现或模拟的是DFA。本节先不论如何从一个正则表达式构建一个有穷自动机，而是讨论如何从一个NFA转换得到相应的DFA。

从NFA转换得到一个DFA通常使用子集构造法（subset construction）。子集构造法的基本思想是让构造得到的DFA的每个状态对应于NFA的一个状态集合，下面对其进行说明。

由NFA构建DFA的子集构造算法，输入一个NFA N，输出一个接受同样语言的DFA D。在此期间会为D构造一个转换表Dtran，D的每个状态是N的状态的一个子集，也就是说，D的一个状态，是在N中从状态s开始经过标号为a或者ε的边能够到达的所有状态的集合，为此，我们需要认识在NFA状态集上的操作：

其中，ε-closure(T)操作的详细过程如下：

我们必须找出当N读入了某个输入串之后可能位于的所有状态集合。首先，在读入第一个输入符号之前，N可以位于集合ε-closure(s0)中的任何状态上（s0是N的初始状态）；接着，假定N在读入串x之后位于集合T中的状态上，如果下一个输入符号为a，那么N可以移动到集合move(T, a)中的任何状态上，又因为N可以在读入a后再执行几个ε转换，所以N在读入串xa后可以位于ε-closure(move(T, a))中的任何状态上。这个过程可以用下面的伪代码表示：

下面我们来实际操作一下。对正则表达式(a|b)*abb，它的一个NFA如下图：

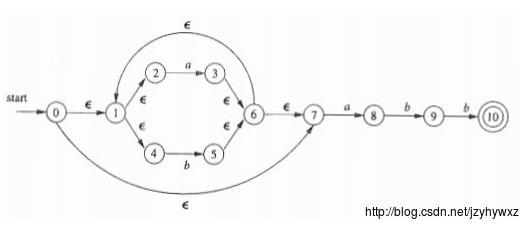
下面我们使用子集构造法构造一个等价的DFA：

1. DFA的初始状态A是ε-closure(0)，即A= 0, 1, 2, 4, 7 ，A中的状态就是从状态0出发，只经过标号为ε的边到达的所有状态；
2. 由于输入符号只有a和b，下面我们计算ε-closure(move(A, a))和ε-closure(move(A, b))，得到Dtran[A, a]=ε-closure(move(A, a))= 1, 2, 3, 4, 6, 7, 8 和Dtran[A, b]=ε-closure(move(A, b))= 1, 2, 4, 5, 6, 7 ，令状态B为Dtran[A, a]，状态C为Dtran[A, b]；
3. 类似第2步，现在我们需要计算ε-closure(move(B, a))、ε-closure(move(B, b))、ε-closure(move(C, a))和ε-closure(move(C, b))，如果出现新的集合，则按照大写字母顺序标记，直到没有新状态产生为止；
4. 把包含NFA终止状态的DFA状态标记为DFA的终止状态。

这样我们就得到了一个等价的DFA，下面是这个DFA及其转换表：

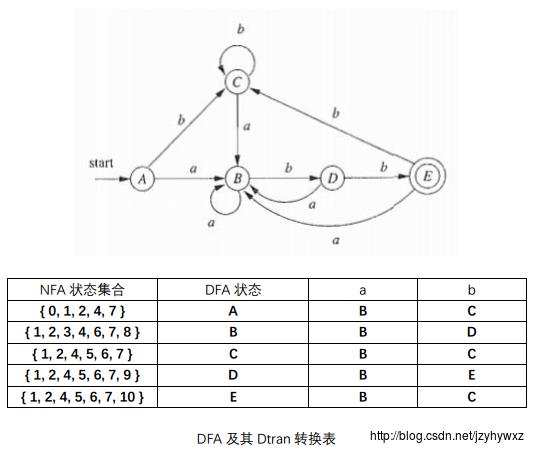
欢迎关注微信公众号fightingZhヾ(◍°∇°◍)ﾉﾞ