二维傅里叶变换滤波/降噪

Posted 2023-04-18

参考技术A

这一篇文章中说明了用"二维卷积"的方法进行滤波/降噪( 二维卷积滤波 )。本文主要介绍另一种滤波的方法：在二维傅里叶变换后的" 频振谱 "中，用" 滤波器 "进行滤波，并对比这两种滤波方法的优劣。

滤波器没那么复杂，就是一个函数式而已，只不过这个函数式有一些特别的功能。本文选用的是" 巴特沃斯滤波器 "；图像的噪声还是" 高斯噪声 "和" 椒盐噪声 "。巴特沃斯滤波器的函数式为：

其中 是截止频率(高于这个频率值，就被滤掉了)， 是阶次， 是" 中心化频振图( 中心化参考这里 ) "中各点" 距中心点的距离 "。非常简单的一个函数。而且注意到： 说明这就是在频域内的一个函数，所以它的用法就是直接和" F(u,v) F频域参看这里 "做" 矩阵点乘 "即可达到滤波~

下面我们就实操一下，对一个原始图像做一下低通滤波看看(把图像" 变模糊 "，因为一些信号被滤掉了)，对应的Matlab程序如下：

效果如下，图1是原始图像，图2是低通滤波后图像(记得ifft2回到原始xy空间)：

利用这篇文章中 同样的噪声 (高斯随机噪声、椒盐噪声)，看看用频域滤波效果如何。这里我就设定截止频率 ，阶次 进行" 巴特沃斯低通滤波 "，加噪声后图像如下：

二维傅里叶变换后频域做低通滤波，效果说明：

最后，再补充一个" 加噪声-fft2-滤波-ifft2 "的完整流程的Matlab程序：

本文用到的" zxc.jpg "原图像， 在这里 。

傅里叶变换滤波之生物信号滤波（笔记03）

1.txt是生物信号的原始信号，2.txt是滤波之后保存的信号

原始信号的片段：

。。。。。。。。。。。。。。。。。。。。。。。

代码：

import matplotlib.pyplot as plt
import numpy as np
import numpy.fft as nf
#傅里叶频率滤波
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示符号
# 读取脉搏信号
#读取信号数据
def readtxt(path):
    with open(path,'r') as f:
        str=f.readline()
        list = str.split(' ')
    list1=[];
    for i,x in enumerate(list):
        if ((i%5 == 0) or (i%5 == 1) or (i%5 == 2)) and x !='':
            list1.append(float(x))
    return list1
#采样频率是500hz
sample_rate=500
#采样长度
noised_sigs=readtxt('1.txt')
times = np.arange(len(noised_sigs)) / sample_rate

plt.figure('Filter')
plt.subplot(221)
plt.title('Time Domain', fontsize=16)
plt.ylabel('Signal', fontsize=12)
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
plt.plot(times[20000:], noised_sigs[20000:], c='orangered', label='脉搏')
plt.legend()
# plt.show()
#基于傅里叶变换，获取频域信息，绘制音频频域的：频率/能量图像
# 傅里叶变换后，绘制频域图像
freqs = nf.fftfreq(times.size, times[20001] - times[20000])
complex_array = nf.fft(noised_sigs)
pows = np.abs(complex_array)

plt.subplot(222)
plt.title('Frequency Domain', fontsize=16)
plt.ylabel('Power', fontsize=12)
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
# 指数增长坐标画图
plt.semilogy(freqs[freqs > 0], pows[freqs > 0], c='limegreen', label='Noised')
plt.legend()
# plt.show()

#将低频噪声去除后绘制信号频域的：频率/能量图像
# where函数寻找那些需要抹掉的复数的索引(获取小于0.5的信号)
noised_indices = np.argwhere(freqs < 0.5)
# 复制一个复数数组的副本，避免污染原始数据
filter_complex_array = complex_array.copy()
filter_complex_array[noised_indices] = 0
filter_pows = np.abs(filter_complex_array)

plt.subplot(223)
plt.xlabel('Frequency', fontsize=12)
plt.ylabel('Power', fontsize=12)
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
plt.plot(freqs[freqs >= 0.2], filter_pows[freqs >= 0.2], c='dodgerblue', label='Filter')
plt.legend()
# plt.show()
#基于逆向傅里叶变换，生成新的信号，绘制时域的：时间/位移图像
filter_sigs = nf.ifft(filter_complex_array).real
plt.subplot(224)
plt.xlabel('Time', fontsize=12)
plt.ylabel('Signal', fontsize=12)
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
plt.plot(times[40000:], filter_sigs[40000:], c='hotpink', label='Filter')
plt.legend()
plt.show()
#写入保存文件
with open('2.txt', 'w') as f:
    str = ' '.join(str(i) for i in filter_sigs)
    f.write(str)

效果展示：

 

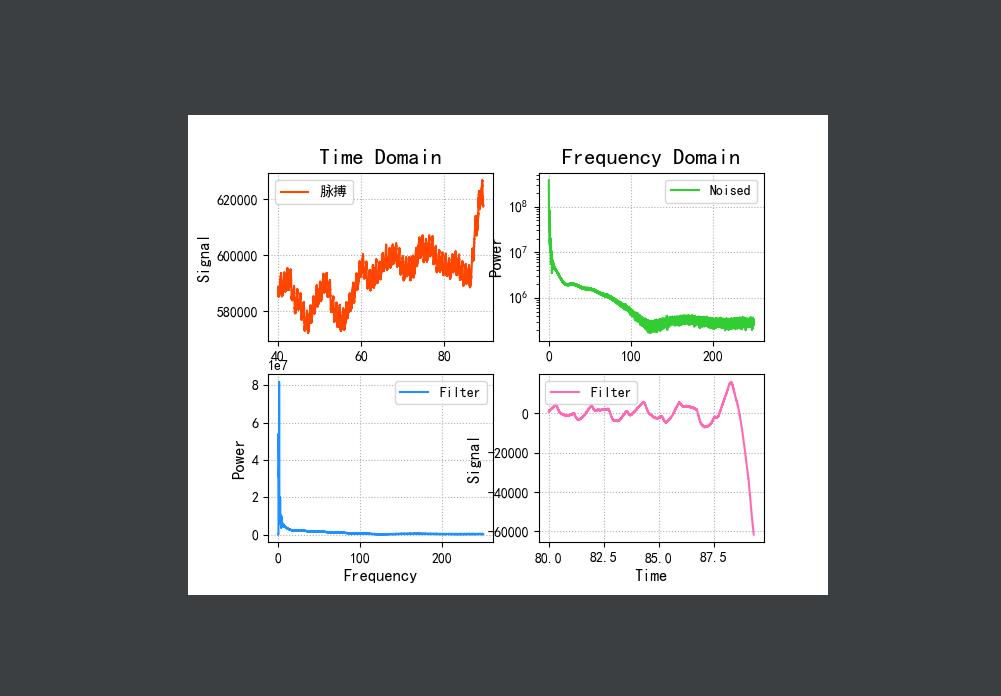
经过滤波我们获取到频率小于0.5的所有信号，左后写入到2.txt的文件内，上图1是原始信号，4是滤波之后的信号。