认识归并排序

Posted 2022-12-02 dxj1016

8、归并排序

先分解，然后合并的时候是先看两边的有没有都越界，没有越界就比较p1和p2的值，哪个小就哪个先放到help中；可能会出现一个越界一个不越界的情况，所以就有两个while判断其中一个不越界的情况，就将元素添加到help新数组中；最后变量help数组中元素将其拷贝到之前的数组中完成排序。

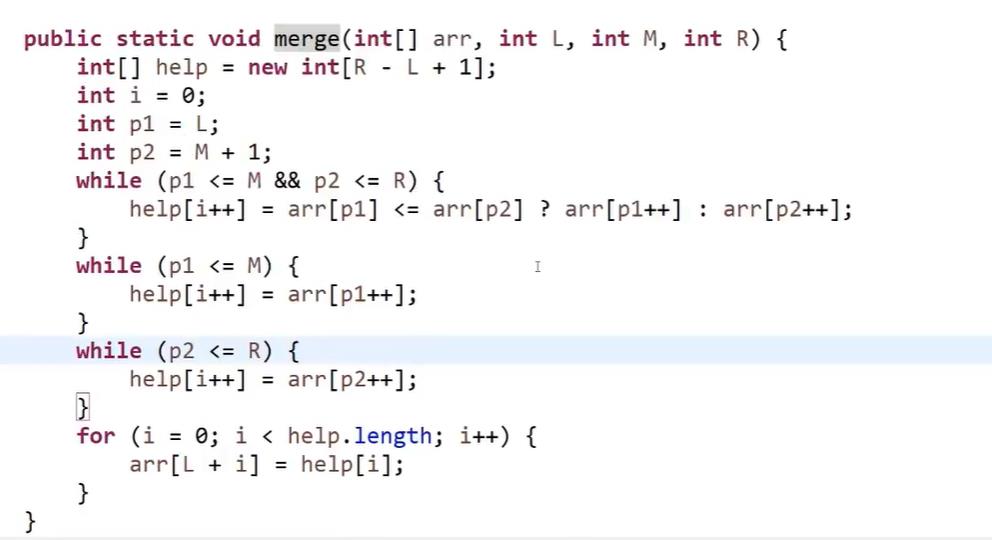
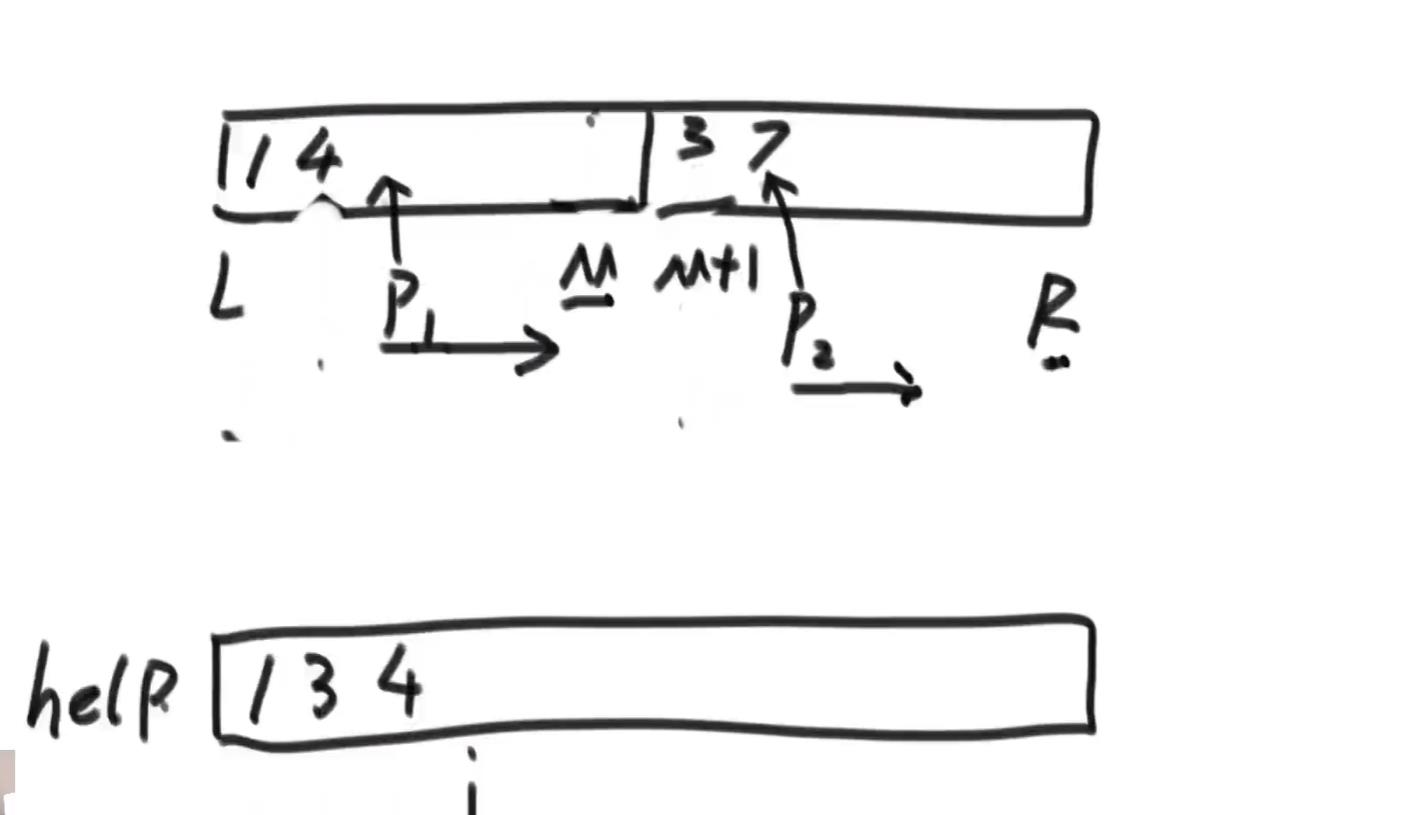
时间复杂度符合master公式；看递归了两次分解函数，而且每次递归规模都是1/2；所以a=2；b=2；然后就看常数项的，主要看 合并函数的时间复杂度了，合并的时候是遍历了整个数组，所以是O(N)，所以d=1；所以可以求出时间复杂度是O(N*logN)

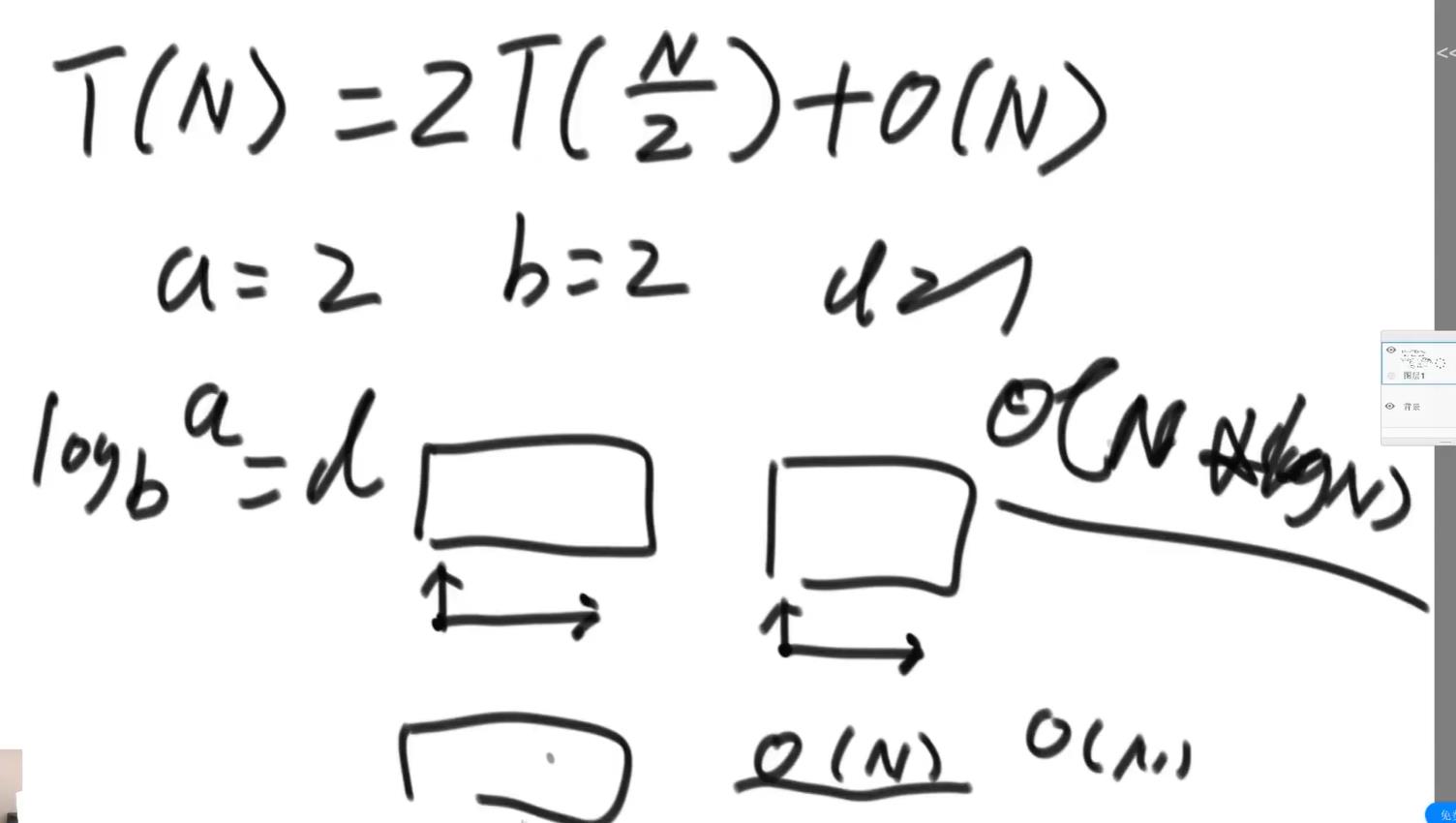
package 左神算法.归并排序;

public class MergeTest 
    public static void main(String[] args) 
        int[] arr = 1, 5, 7, 3, 0, 9, 4;
        int L = 0;
        int R = arr.length - 1;
        process(arr, L, R);
    

    public static void process(int[] arr, int L, int R) 
        if (L == R) 
            return;
        
        int mid = L + ((R - L) >> 1);
        process(arr, L, mid);
        process(arr,mid+1,R);
        merge(arr, L, mid, R);
    

    public static void merge(int[] arr, int L, int M, int R) 
        int[] help = new int[R - L + 1];
        int i = 0;
        int p1 = L;
        int p2 = M + 1;
        while (p1 <= M && p2 <= R) 
            help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
        
        while (p1 <= M) 
            help[i++] = arr[p1++];
        
        while (p2 <= R) 
            help[i++] = arr[p2++];
        
        for (i = 0; i < help.length; i++) 
            arr[L + i] = help[i];
        
    

8.1、归并排序的扩展

8.2、小和问题

小和问题可以转换为在1的时候，右边有多少个数比他大，所有有4个1；到3 的时候右边有两个比3大，所以就是有2个3；在4的时候右边有一个比4大，所以就是1个4；到2的时候有一个比2大，所以就一个2；到5的时候右边没有了，所以就前面的4个1加上2个3加上1个4加上1个2：1+1+1+1+3+3+4+2=16；

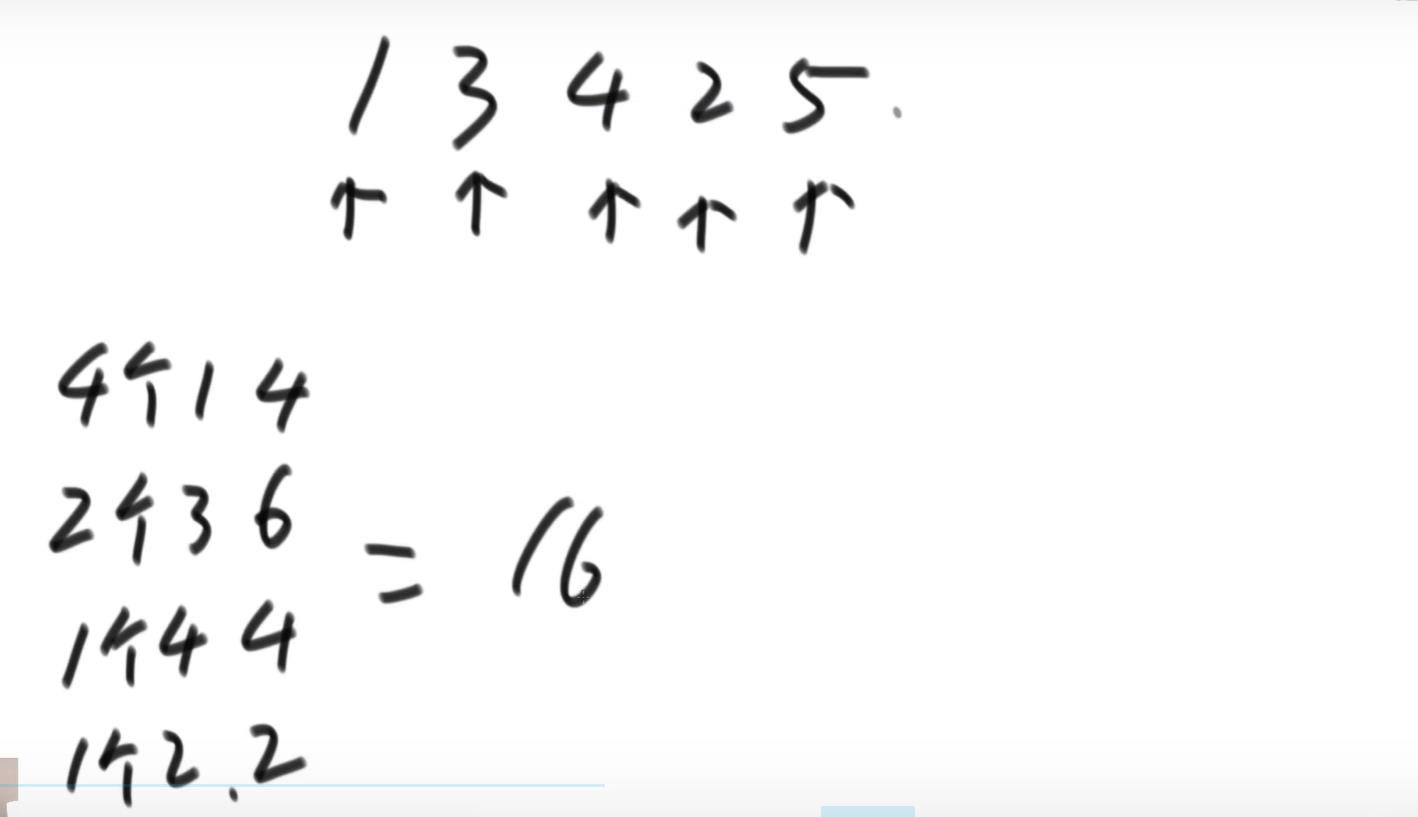
可以使用归并排序的思路进行求解这个小和问题：首先数组元素先分解，然后合并，合并的时候首先是看左边的数和右边的数对比，哪个小就加入新的数组中，如果是左边的小，比较一次就有一个该元素的值。

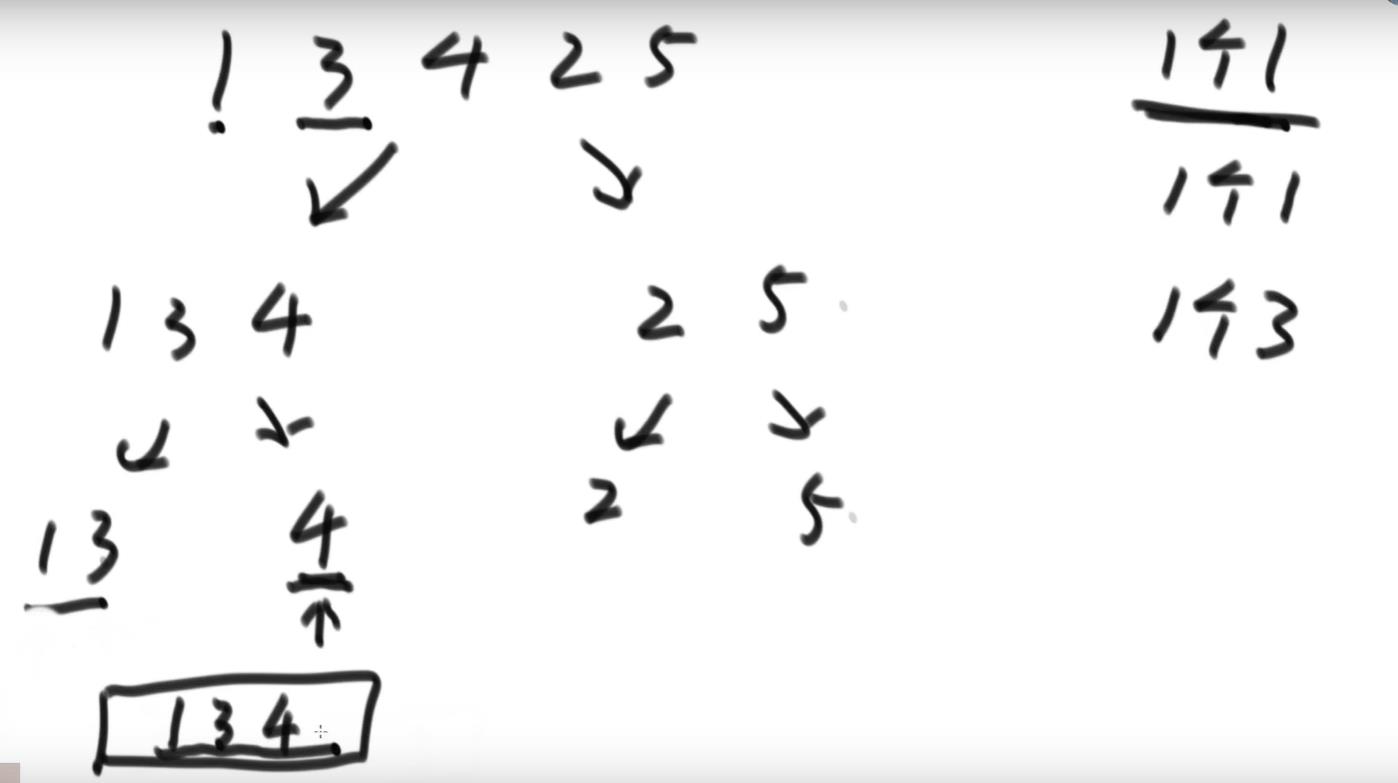
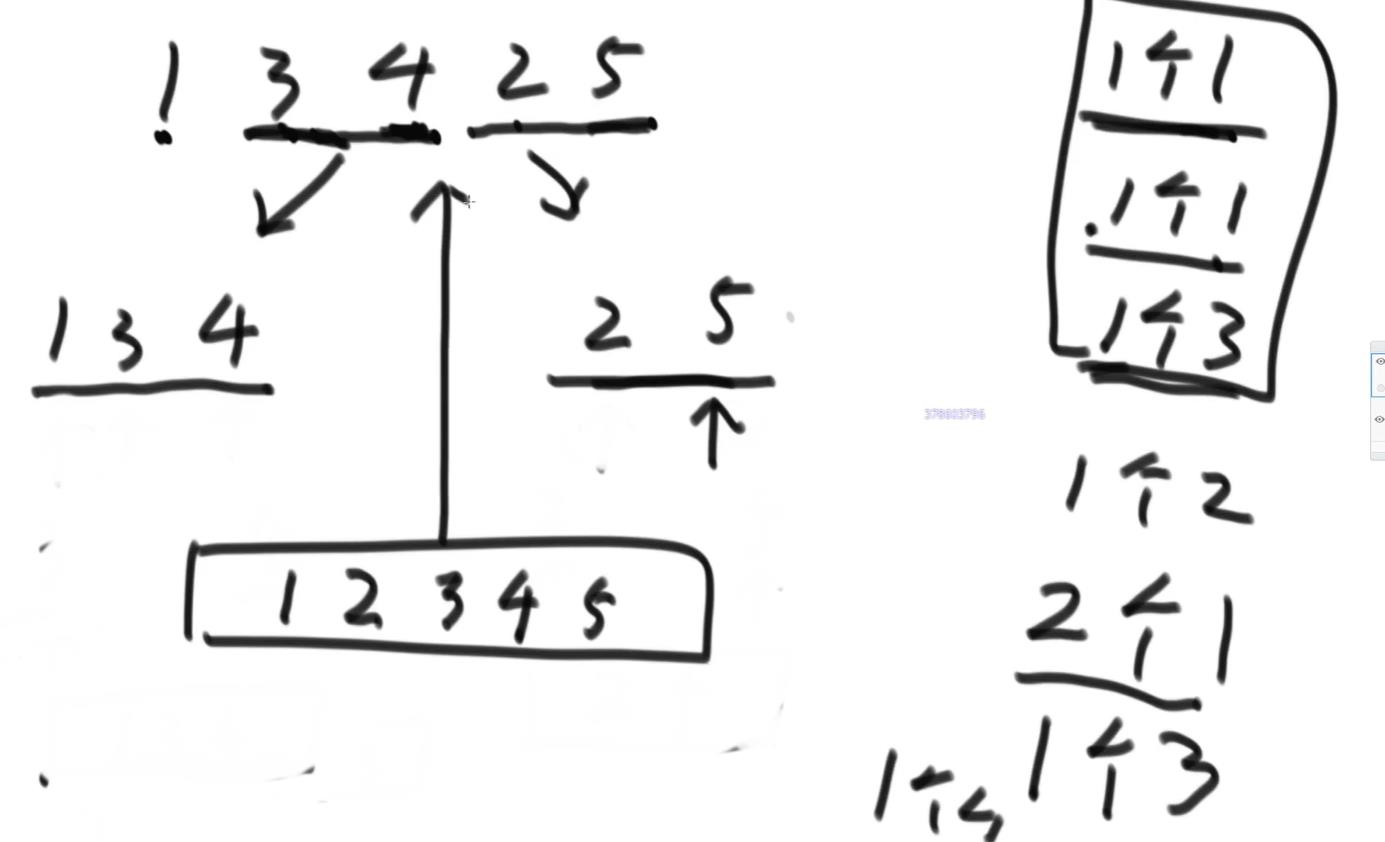
这里的合并过程跟归并排序的经典合并过程有一点不一样：在归并排序的时候合并的时候当左边的和右边的数一样的时候，是先拷贝左边的值到新的数组中；但是这里的合并过程当左边和右边的值一样的时候，是先将右边的值拷贝到新的数组中。

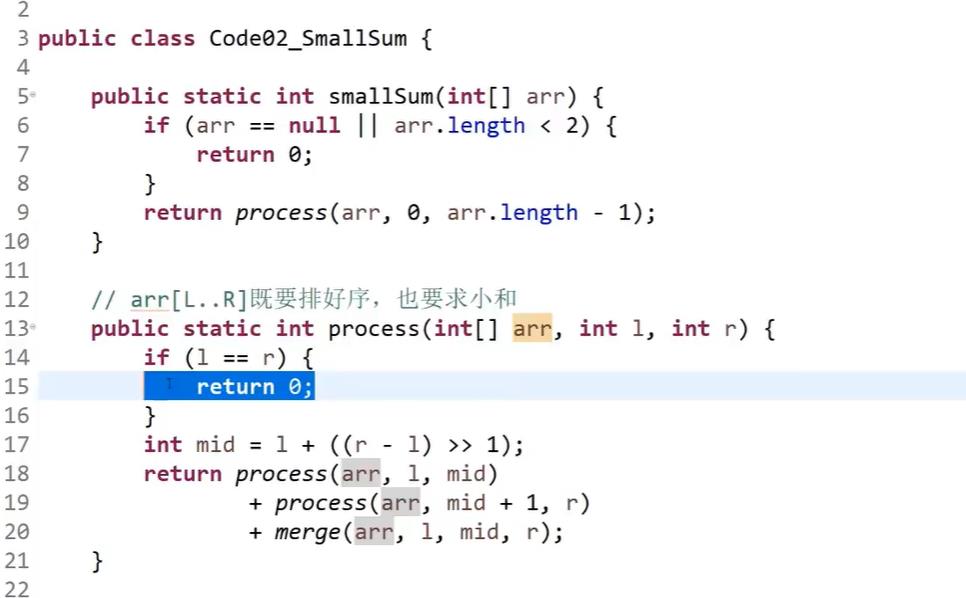
小和问题的代码如下：

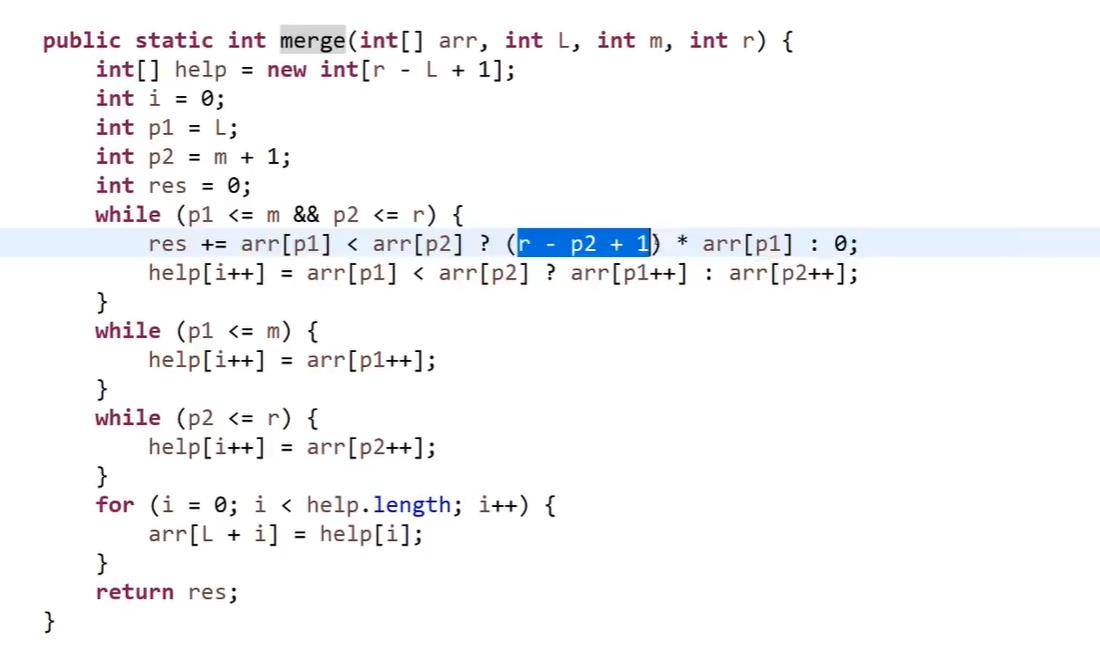
8.3、逆序对问题

在3的时候，3比右边的数大的有2和0，所以就有逆序对3,2和3,0；2比右边的数大的只有0，所以就有逆序对2,0；4比右边的数大的只有0，所以就有逆序对4,0；5比右边的数大的只有0，所以就有逆序对5,0；

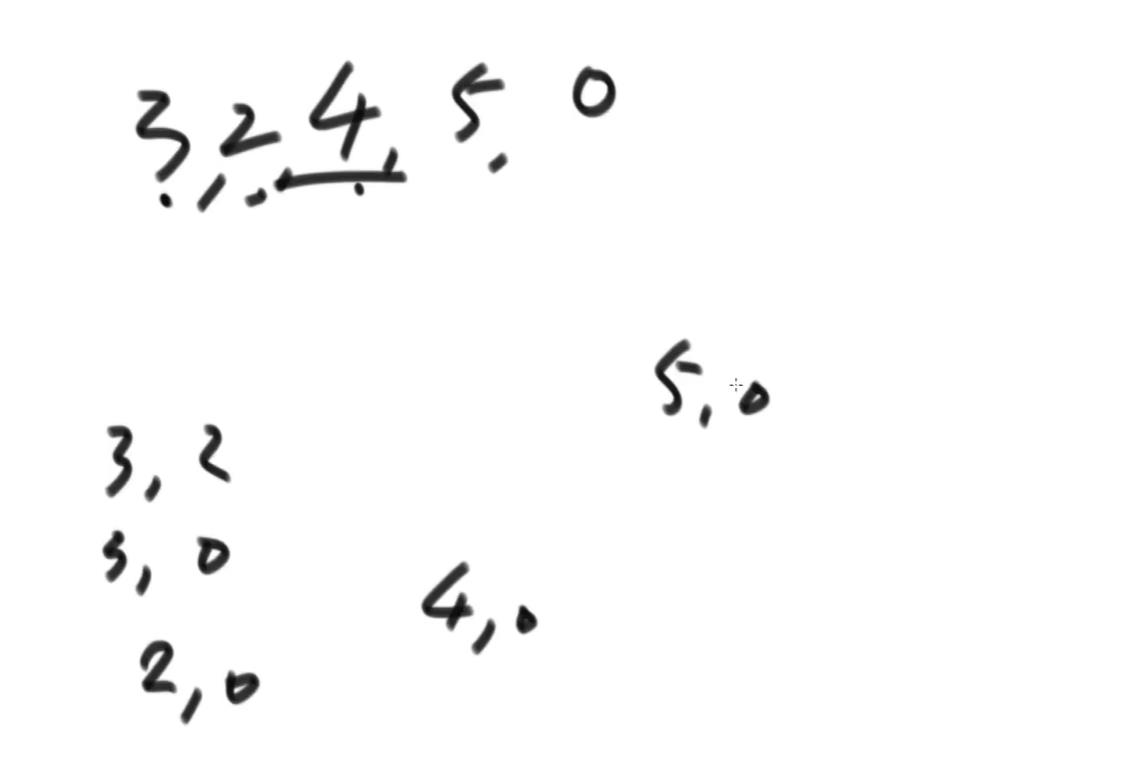
最小和问题和逆序对问题的代码实现如下：

package 左神算法.归并排序;

public class SmallSum 
    public static void main(String[] args) 
        int[] arr = 3, 2, 1, 2, 5, 4, 9;
        System.out.println(smallSum(arr));
    

    public static int smallSum(int[] arr) 
        if (arr == null || arr.length < 2) 
            return 0;
        
        return process(arr, 0, arr.length - 1);
    
//   arr[L..R]既要排好序也要求最小和
    public static int process(int[] arr, int l, int r) 
        if (l == r) 
            return 0;
        
        int mid = l + ((r - l) >> 1);
        return process(arr, l, mid) + process(arr, mid + 1, r) + merge(arr, l, mid, r);
    

    public static int merge(int[] arr, int L, int m, int r) 
        int[] help = new int[r - L + 1];
        int i = 0;
        int p1 = L;
        int p2 = m + 1;
        int res = 0;
        while (p1 <= m && p2 <= r) 
//            res += arr[p1] < arr[p2] ? (r - p2 + 1) * arr[p1] : 0;//求最小和
            res += arr[p1] > arr[p2] ? (m-p1+1)  : 0;//求逆序对
            help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
        
        while (p1 <= m) 
            help[i++] = arr[p1++];
        
        while (p2 <= r) 
            help[i++] = arr[p2++];
        
        for (i = 0; i < help.length; i++) 
            arr[L + i] = help[i];
        
        return res;
    

package 左神算法.归并排序;

public class SmallSum 
    public static void main(String[] args) 
        int[] arr = 3, 2, 1, 2, 5, 4, 9;
        smallSum(arr);

    

    public static void smallSum(int[] arr) 
        if (arr == null || arr.length < 2) 
            return;
        
       process(arr, 0, arr.length - 1);
    
//   arr[L..R]既要排好序也要求最小和
    public static void process(int[] arr, int l, int r) 
        if (l == r) 
            return;
        
        int mid = l + ((r - l) >> 1);
        process(arr, l, mid);
        process(arr, mid + 1, r);
        merge(arr, l, mid, r);
    

    public static void merge(int[] arr, int L, int m, int r) 
        int[] help = new int[r - L + 1];
        int i = 0;
        int p1 = L;
        int p2 = m + 1;
        int res = 0;
        while (p1 <= m && p2 <= r) 
//            res += arr[p1] < arr[p2] ? (r - p2 + 1) * arr[p1] : 0;//求最小和
//            res += arr[p1] > arr[p2] ? (m-p1+1)  : 0;//求逆序对的对数
            if (arr[p1] > arr[p2]) 
                for (int k = p1; k <= m; k++) 
                    System.out.println("(" + arr[k] + "," + arr[p2] + ")");
                
            
            help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
        
        while (p1 <= m) 
            help[i++] = arr[p1++];
        
        while (p2 <= r) 
            help[i++] = arr[p2++];
        
        for (i = 0; i < help.length; i++) 
            arr[L + i] = help[i];
        
//        return res;
    

/*
(3,2)
(2,1)
(3,1)
(5,4)
*/

8.4、荷兰问题

问题一：给定一个数组arr， 和一个数num， 请把小于等于num的数放在数组的左边， 大于num的数放在数组的右边。

额外空间复杂度O(1)， 时间复杂度O(N)。分析：只说大于的在右边，没要求有序。

方法：

（1）设置一个指针X，指向数组前一个元素

（2）遍历数组，如果数组元素小于给定的数num，那么数组元素和小于等于区域的下一个数交换，然后小于等于区右扩X++，然后到数组下一个元素i++；

（3）如果数组元素大于给定的数num，那么X不变，继续遍历下一个元素i++；

比如数组1,5,4,8,3,2；X一开始为-1，num为5，遍历数组元素，

第一个元素1,1<5，所以1和X下一个元素交换位置，那就是1和1交换位置还是1，X+1=0，i++=1；1,|5,4,8,3,2

第二个元素5没有小于5，所以不交换，直接遍历下一个元素i++=2；

第三个元素4<5，所以X+1=1，所以4和X=1位置的5交换位置，X=1，i++=3；1,4,|5,8,3,2

第四个元素8>5，所以不交换元素，遍历下一个元素i++；

第五个元素3<5，3和x+1=2位置的5交换位置，X=2，i++=4；最后元素为：1,4,3,|8,5,2

第六个元素2<5,2和x+1=3位置的8交换位置，X=3，i++=5；最后元素为：1,4,3,2,|5,8

问题二：

（1）设置一个指针X，指向数组前一个元素；设置一个指针Y，指向数组最后一个元素的后一个元素；

（2）遍历数组，如果数组元素小于给定的数num，那么数组元素和小于等于区域的下一个数交换，然后小于等于区右扩X++，然后到数组下一个元素i++；

（3）如果数组元素大于给定的数num，那么数组元素和大于区域的前一个元素交换，然后大于区域左扩Y–，继续遍历下一个元素i++；

（4）如果数组元素等于给定的数num，那么不交换元素，直接遍历下一个元素i++；

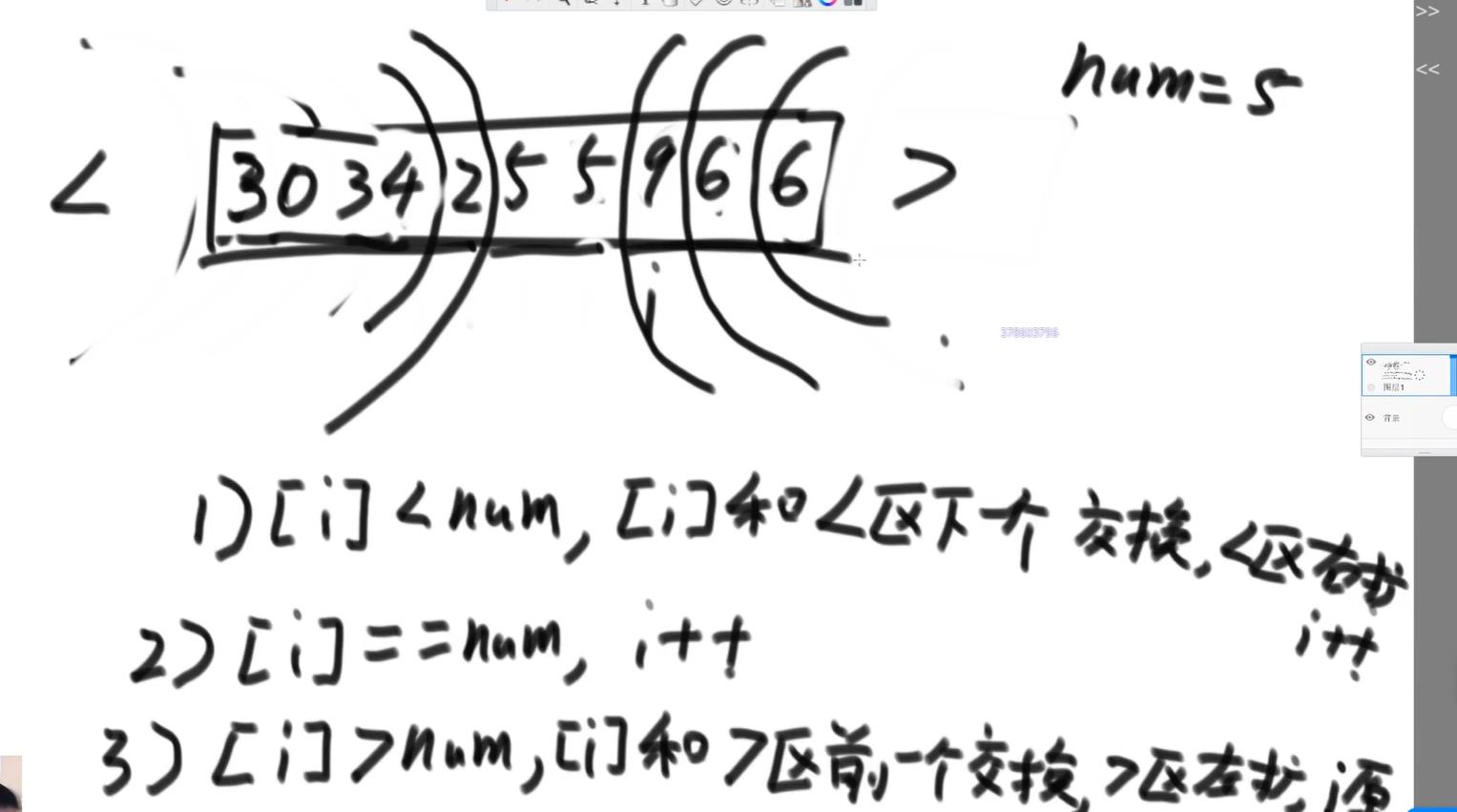
过程：3,5,0,3,4,5,2,6,9,6；第一次：3,|5,0,3,4,5,2,6,9,6；第二次：3,|5,0,3,4,5,2,6,9,6；第三次：3,0,|5,3,4,5,2,6,9,6第四次：3,0,3,|5,4,5,2,6,9,6；第五次：3,0,3,4,|5,5,2,6,9,6；第六次：3,0,3,4,|5,5,2,6,9,6

第七次：3,0,3,4,2,|5,5,6,9,6；第八次：3,0,3,4,2,|5,5,6,9|,6；第九次：3,0,3,4,2,|5,5,9,|6,6；第十次：3,0,3,4,2,|5,5,|9,6,6

package 左神算法.归并排序;

public class HeLan 
    public static void main(String[] args) 
        int[] arr = 1, 5, 4, 8, 3, 2;
        partSort1(arr, 5);
        int[] arr2 = 3, 5, 0, 3, 4, 5, 2, 6, 9, 6;
//        int[] arr2 = 1,5,4,8,3,5,9,5,6,2;
        partSort2(arr2, 5);
        for (int i = 0; i < arr.length; i++) 
            System.out.print(arr[i] + " ");
        
        System.out.println();
        for (int i = 0; i < arr2.length; i++) 
            System.out.print(arr2[i] + " ");
        


    
//小于等于num的在左边，大于num的在右边
    public static void partSort1(int[] arr, int num) 
        int X = -1;
        for (int i = 0; i < arr.length; i++) 
            if (arr[i] < num) 
                swap(arr, i, X + 1);
                X++;
            
        
    
//小于的在num左边，等于的在中间，大于的在num右边
    public static void partSort2(int[] arr, int num) 
        int X = -1;
        int endIndex = arr.length;
        for (int i = 0; i < endIndex; i++) 
            if (arr[i] == num) 
                continue;
             else if (arr[i] < num) 
                swap(arr, i, X + 1);//和小于域的后一个位置的元素交换，叩打小于域
                X++;
             else 
                swap(arr, i, endIndex - 1);//和大于域的前一个位置的元素交换，扩大大于域
                endIndex--;
                i--;//交换之后，还得在原位置再比一次,因为交换后那个元素还不知道是否比num大
                /*
                 * X那不减，是因为：X~i之间的元素已经比较过了
                 * 但是endIndex这边，i~endIndex之间的数都没比过，所以交换了endIndex的前一个位置的元素后，还得比一次
                 */
            
        
    
//交换两个元素
    public static void swap(int[] arr, int i, int j) 
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;