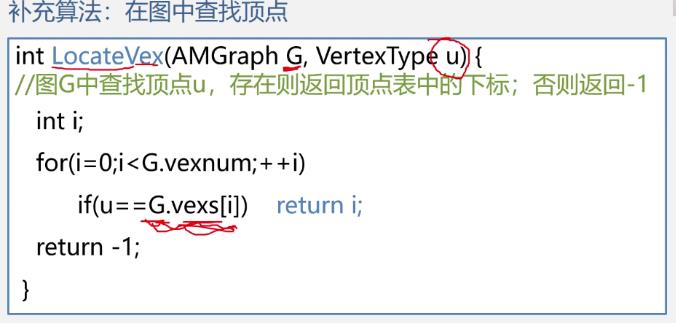
数据结构与算法学习笔记 图
Posted 临风而眠
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构与算法学习笔记 图相关的知识,希望对你有一定的参考价值。
数据结构与算法学习笔记(8) 图
复习
文章目录
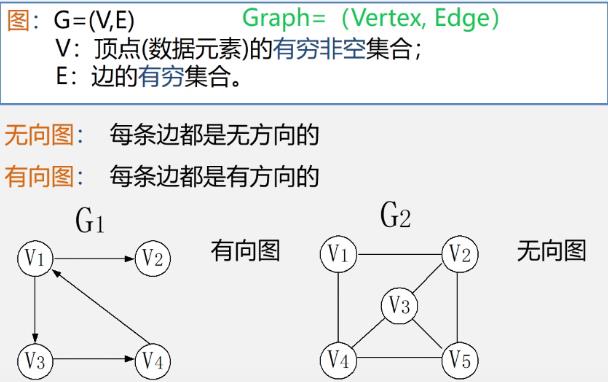
一.图的定义和基本术语
-
图、无向图、有向图
-
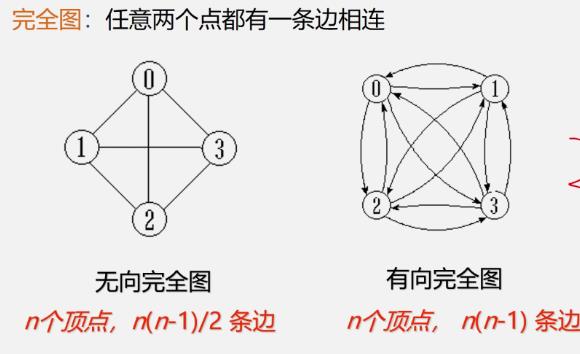
完全图
-
稀疏图、稠密图、网、邻接、关联

- 顶点的度
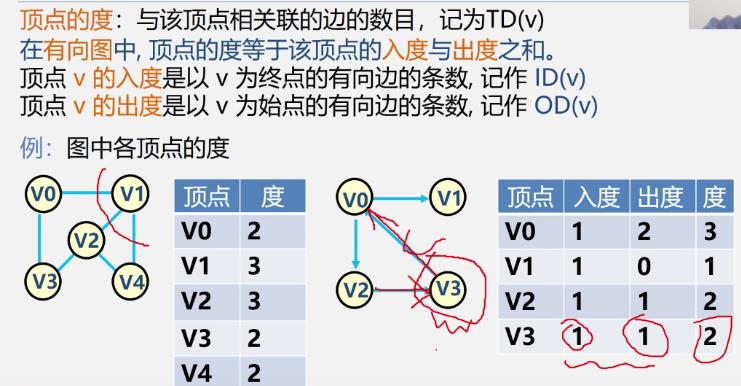
-
有向树
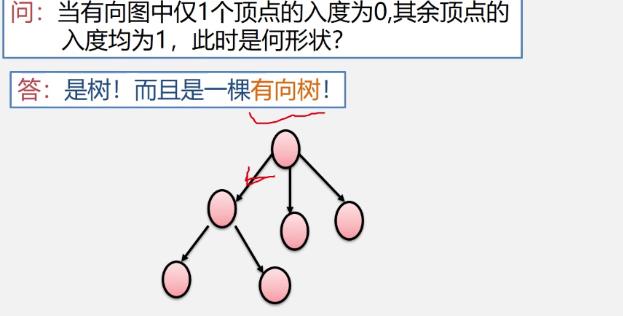
-
路径、路径长度、回路、简单路径、简单回路
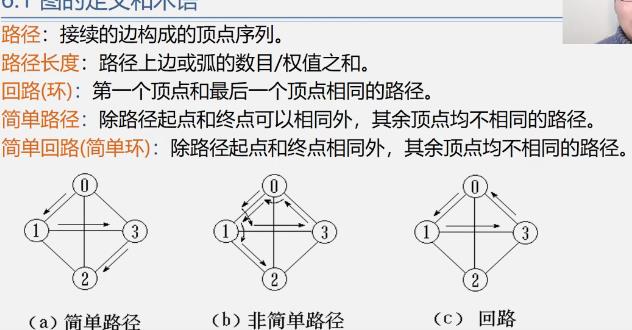
-
连通图
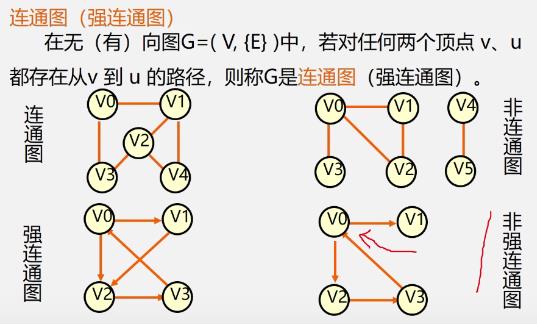
-
权、网

-
子图
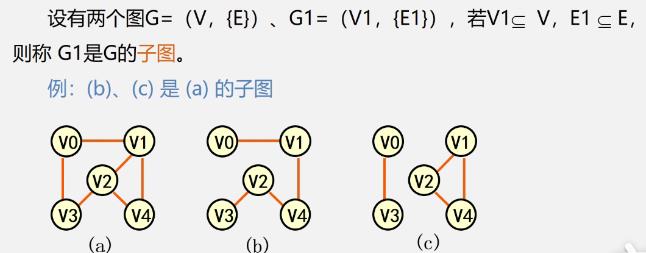
-
连通分量、极大连通子图、极小连通子图、生成树、生成森林
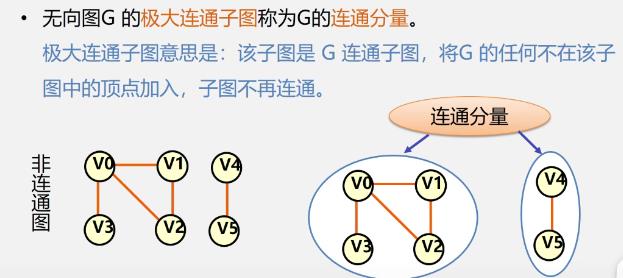
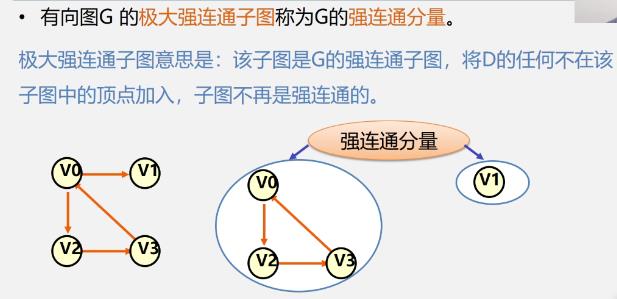
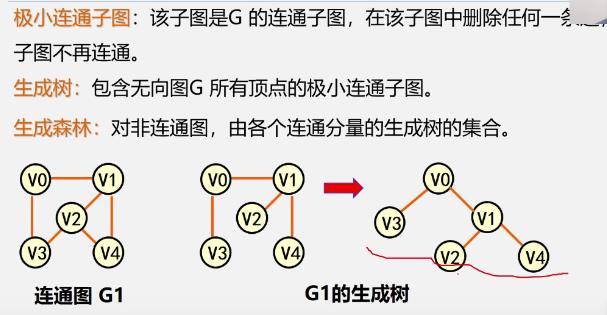
二.图的类型定义



三.图的存储结构
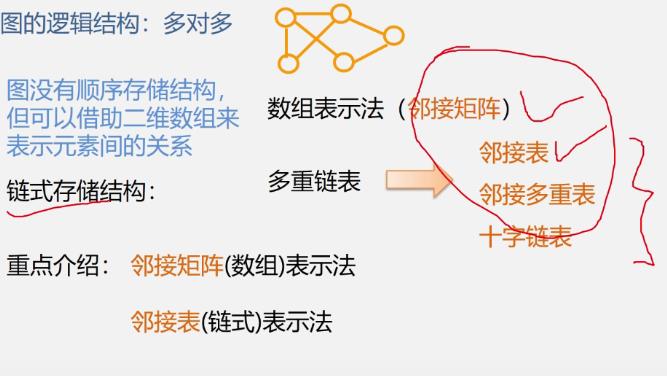
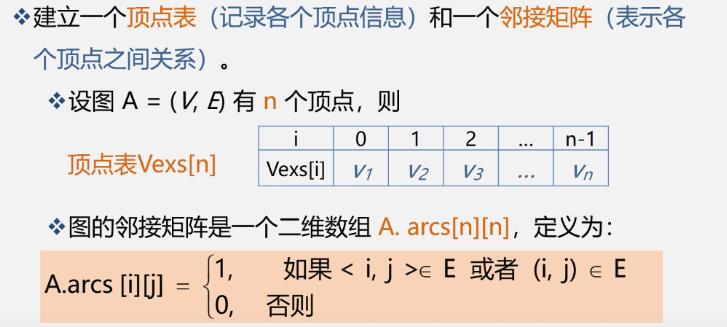
1.邻接矩阵
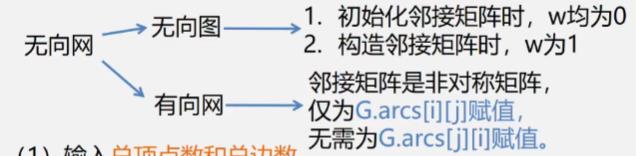
无向图的邻接矩阵

有向图的邻接矩阵
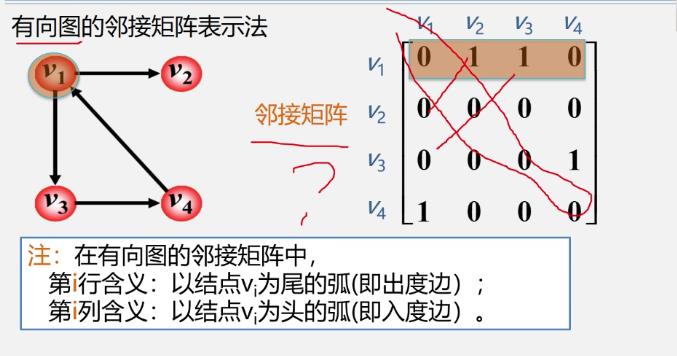
第i行:以结点 v i v_i vi为头,结点 v j ( j = 1 , 2 , 3 , . . . , n ) v_j(j=1,2,3,...,n) vj(j=1,2,3,...,n)为尾的弧
第i列:以结点 v i v_i vi为尾,结点 v j ( j = 1 , 2 , 3 , . . . , n ) v_j(j=1,2,3,...,n) vj(j=1,2,3,...,n)为头的弧

网(有权图)
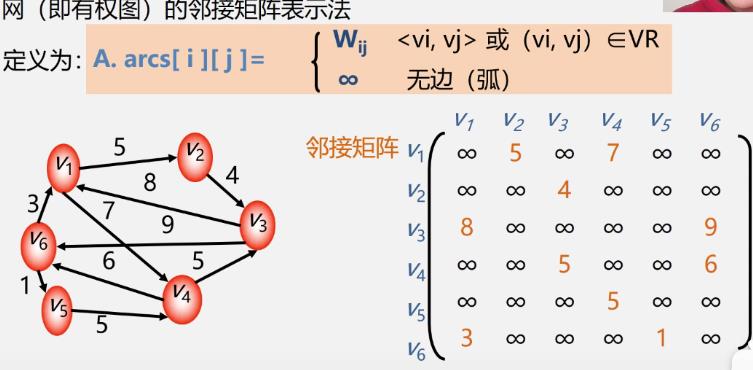
邻接矩阵的存储表示
-
用两个数组分别存储顶点表和邻接矩阵

创建邻接矩阵(以无向网为例)

- 算法描述


邻接矩阵表示法的优缺点
-
优点

-
缺点

2.邻接表
链式存储结构
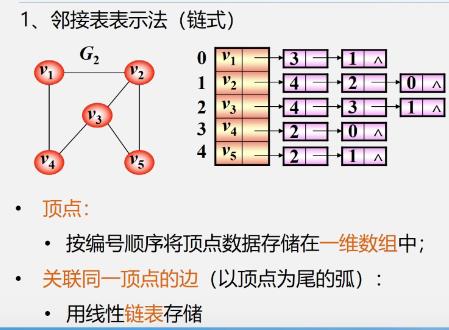
-
头结点

-
表结点
adjacent 相邻的
vertex 顶点
arc 弧

-
adjvex:邻接点域,存放与 v i v_i vi邻接的顶点在表头数组中的位置
-
nextarc:链域,指示下一条边或弧
如果每一条边还有权值的话,可以增加一个数据域

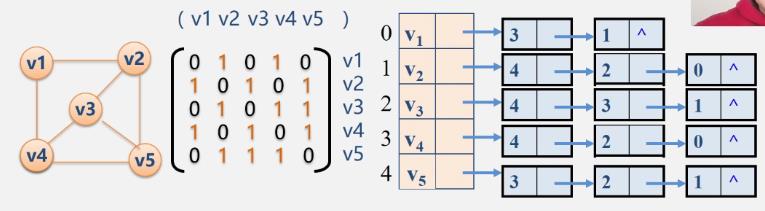
无向图的邻接表
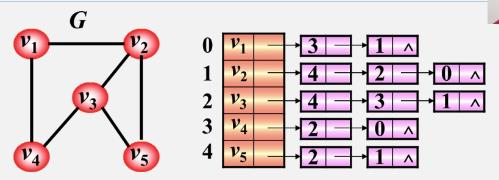
-
特点
-
邻接表不唯一
比如上面那个v1后面的3和1可以互换
-
若无向图中有n个顶点、e条边,则其邻接表需n个头结点和2e个表结点,适宜存储稀疏图
-
无向图中顶点 v i v_i vi的度为第i个单链表中的结点数
-
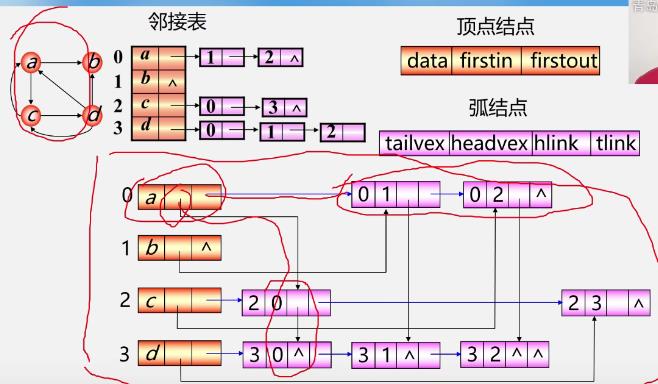
有向图的邻接表
-
邻接表
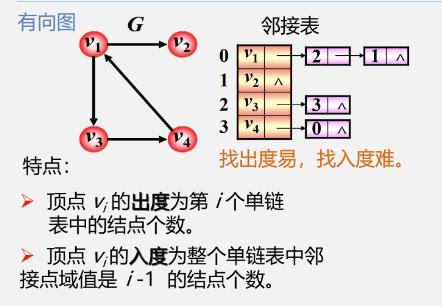
-
逆邻接表
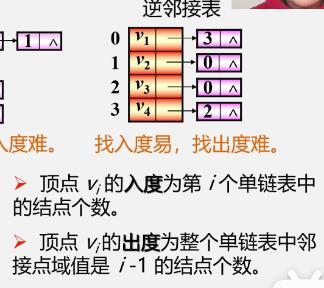
-
例
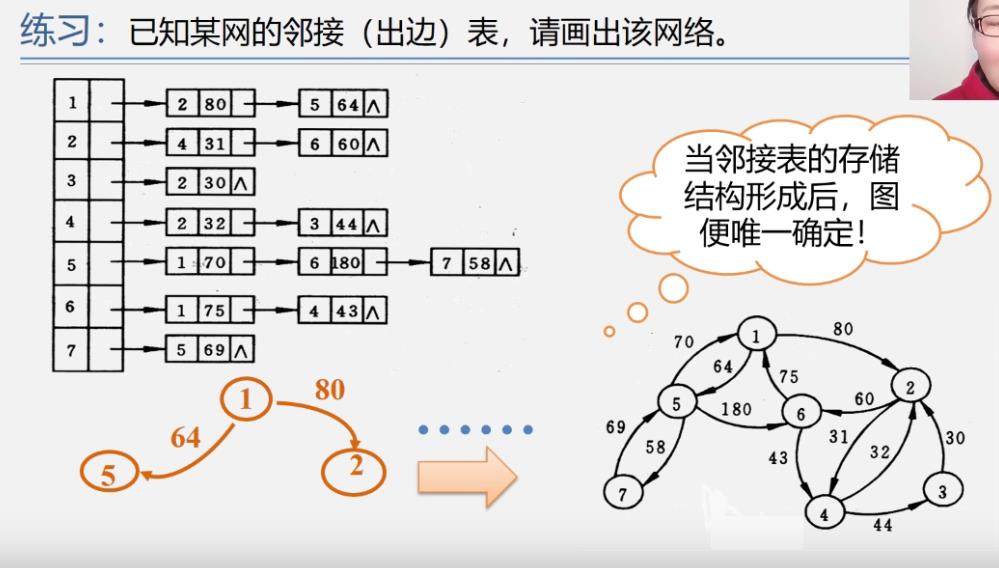
建立邻接表的算法
-
顶点的结点结构

typedef struct VNode VerTexType data; //顶点信息 ArcNode * firstarc; //指向第一条依附该顶点的边的指针 VNode,AdjList[MVNum]; //AdjList表示邻接表类型
-
边结点结构

#define MVNum 100 //最大顶点数 typedef struct ArcNode//边结点 int adjvex; //该边所指向的顶点的位置 struct ArcNode * nextarc; //指向下一条边的指针 OtherInfo info; //与边相关的信息 ArcNode; -
图的结构定义
typedef struct AdjList vertices; int vexnum,arcnum; //图的当前顶点数和弧数 ALGraph;-
邻接表操作举例
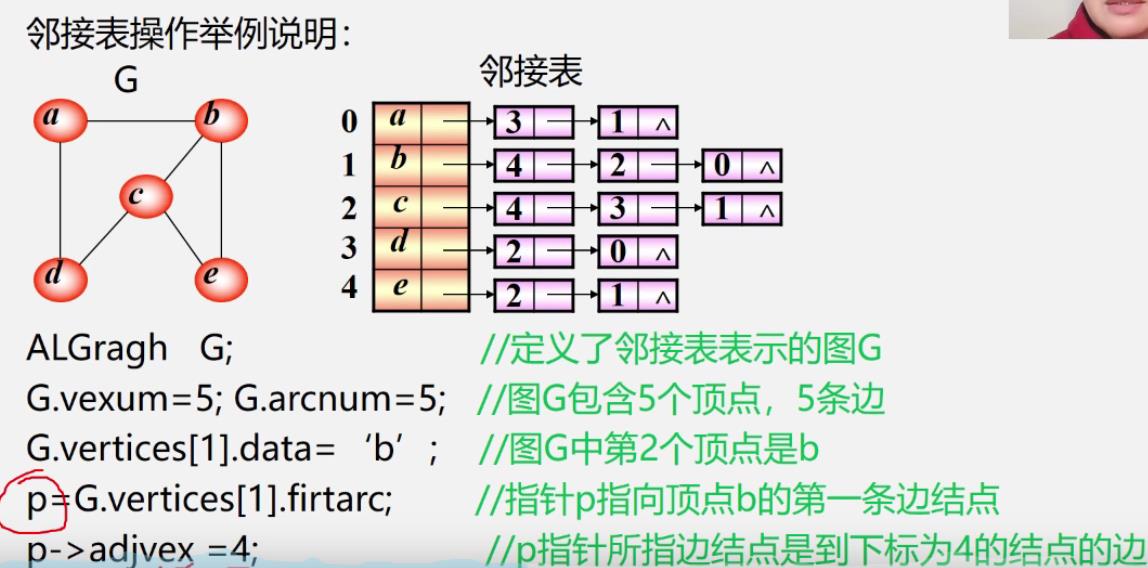
-
用邻接表表示法创建无向网
-
算法思想

-
算法描述


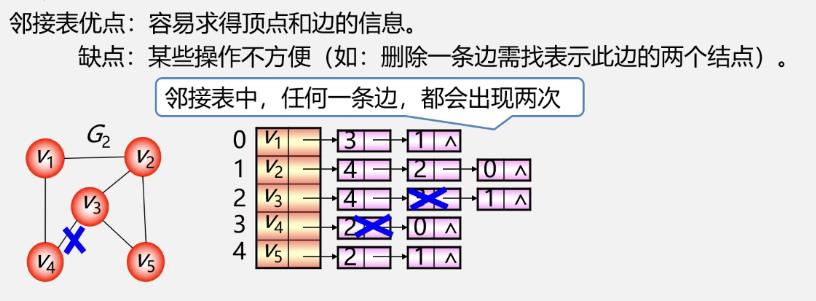
邻接表优缺点
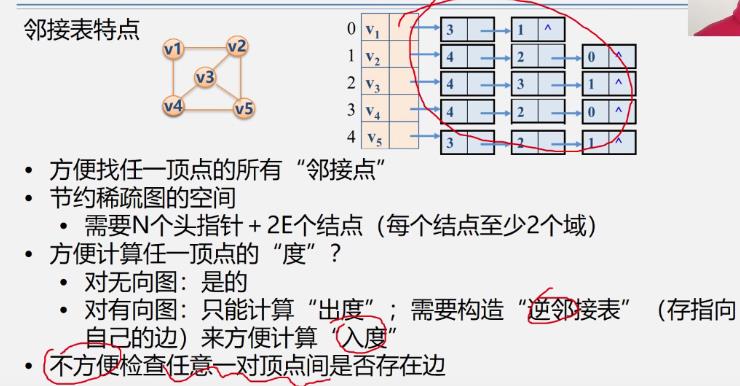
邻接表、邻接矩阵


3.十字链表(用于有向图)
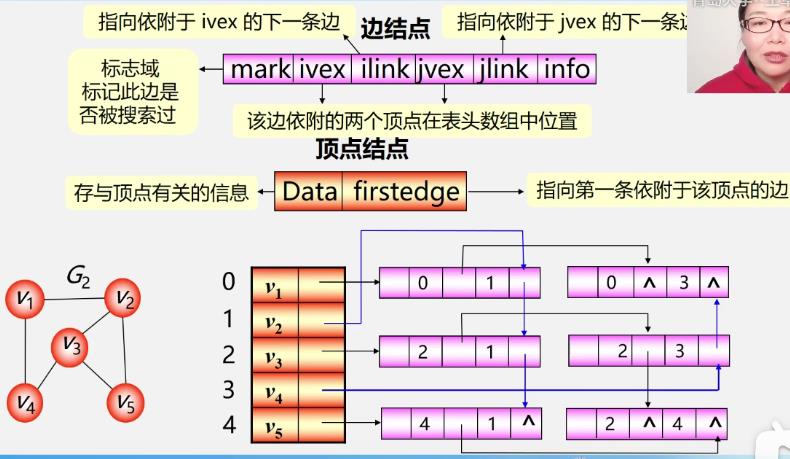
4.多重邻接表(无向图的另一种链式存储结构)
四.图的遍历
-
遍历定义

-
遍历实质
找每个顶点的邻接点的过程

1.深度优先搜索(DFS)
-
算法思想

-
例
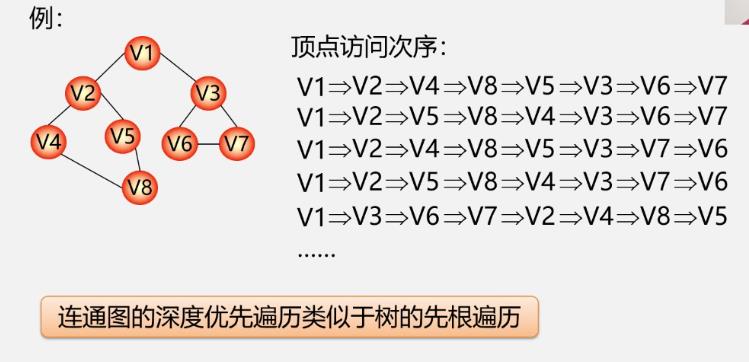
邻接矩阵实现深度优先搜索遍历
-
例
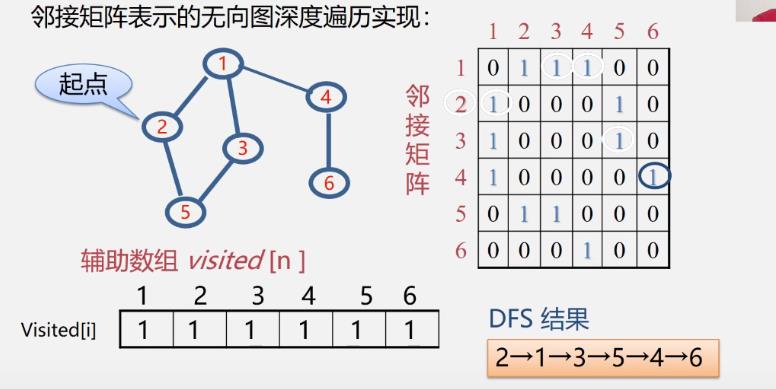
-
算法描述

邻接表实现深度优先搜素
-
算法效率分析

2.广度优先搜索(BFS)
-
算法思想

-
算法
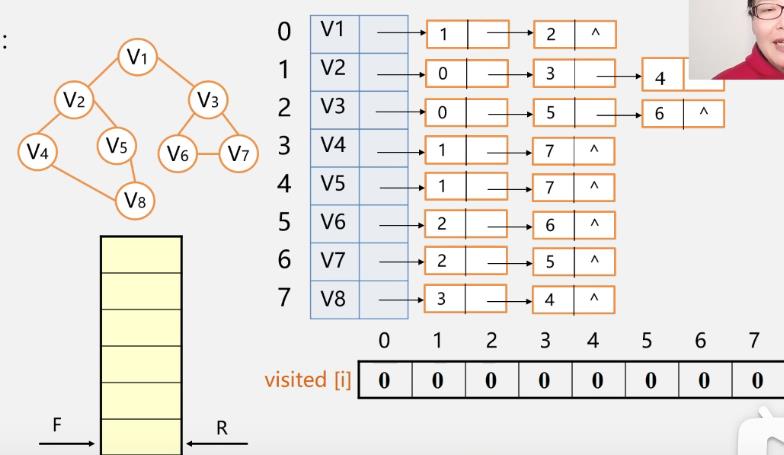
利用队列
-
算法描述
按广度优先非递归遍历连通图G
void BFS(Graph G,int v) //按广度优先非递归遍历连通图G cout<<v; visited[v] = true; //访问第v个顶点 InitQueue(Q); //辅助队列Q初始化,置空 EnQueue(Q,v); //v进队 while(!QueueEmpty(Q)) //队列非空 DeQueue(Q,u); //队头元素出队并置为u for(w = FirstAdjVex(G,u);w>=0; w = NextAdjVex(G,u,w)) //NextAdjvex:找下一个顶点 if(!visited[w]) //w为u的尚未访问过的邻接顶点 cout<<w; visited[w]=true; EnQueue(Q,w); //w进队 //BFS -
算法效率分析

3.DFS与BFS算法效率比较

五.图的应用
1.最小生成树
①生成树概念回顾
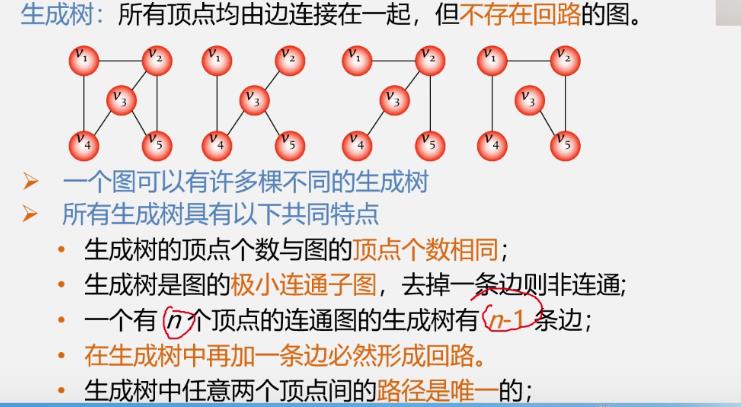
-
注:
含n个顶点n-1条边的图不一定是生成树,如:
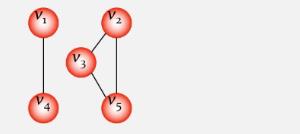
无向图的生成树


②最小生成树及其应用
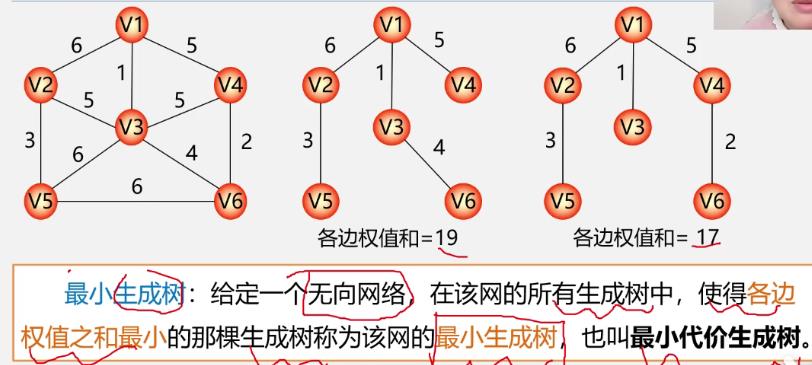
-
应用举例

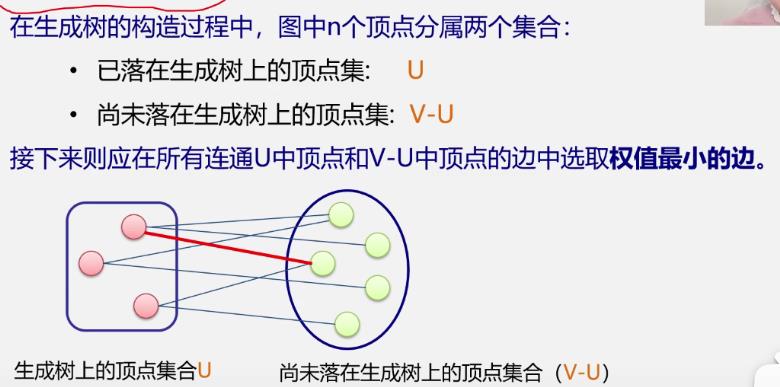
③构造最小生成树
MST性质
Minimum Spanning Tree

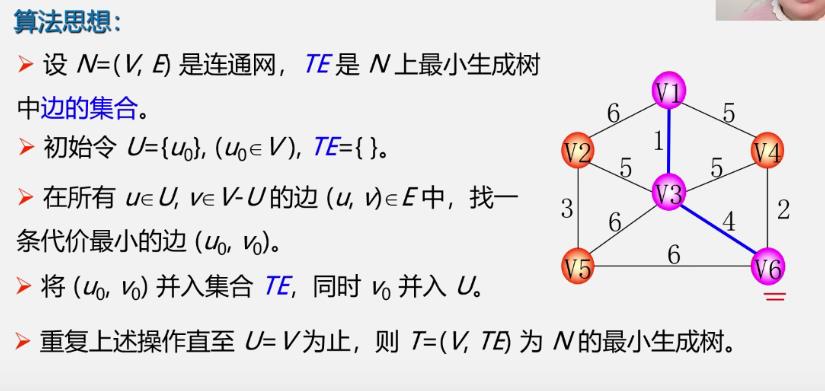
算法一:Prim(普里姆)算法
算法二:Kruskal(克鲁斯卡尔)算法

最小生成树可能不唯一
两种算法比较

2.最短路径
典型应用

问题求解

第一类:两点间的最短路径
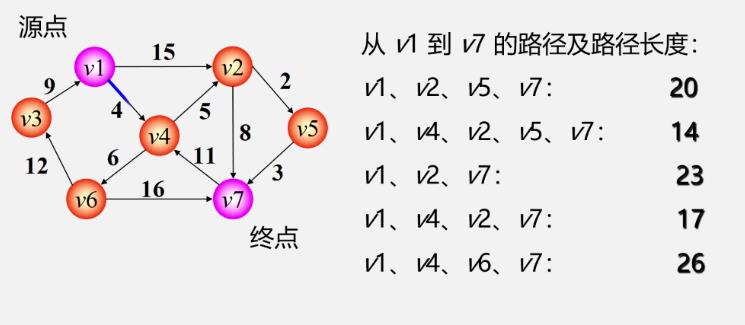
第二类:某源点到其他各地的最短路径
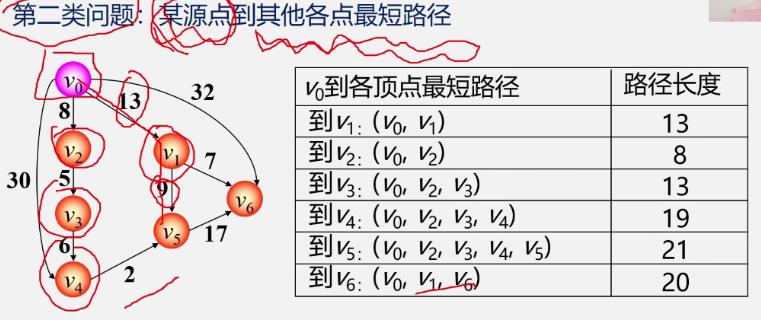
两类问题的求解算法
单源最短路径-Dijkstra(迪杰斯特拉)算法


-
具体步骤
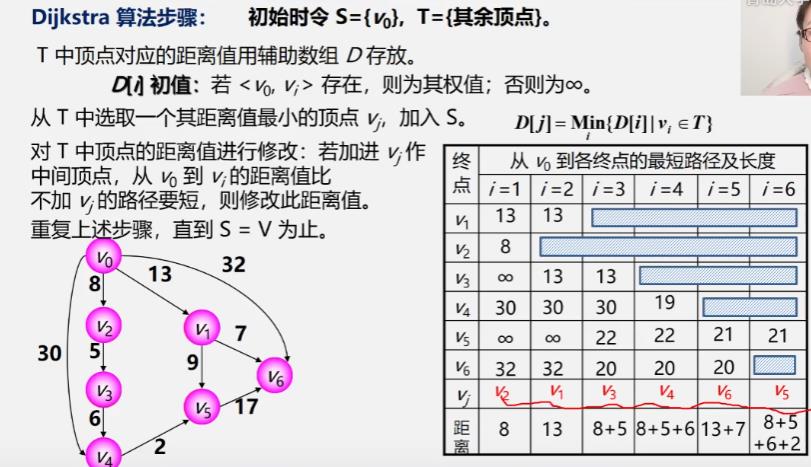
所有顶点间的最短路径-Floyd(弗洛伊德)算法

Dijkstra算法时间复杂度O(n²),执行n次相当于O(n³)
Floyd算法时间复杂度O(n³)
-
算法思想

-
算法步骤
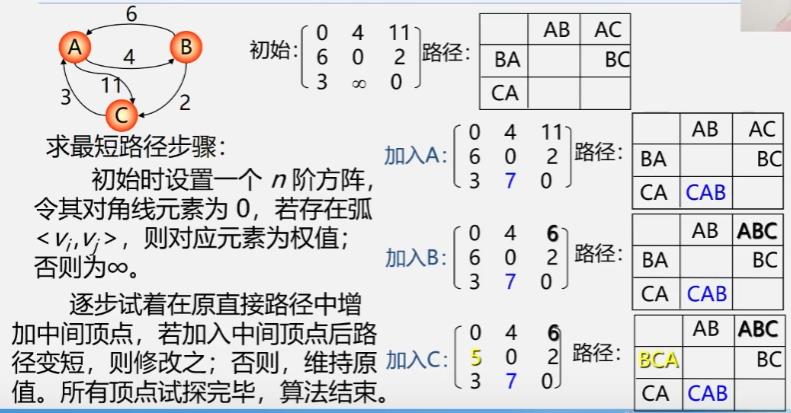
3.拓扑排序
针对有向无环图
有向无环图及其应用
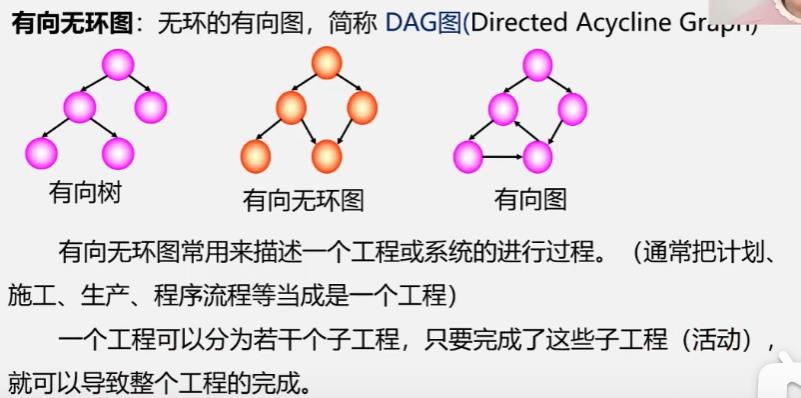
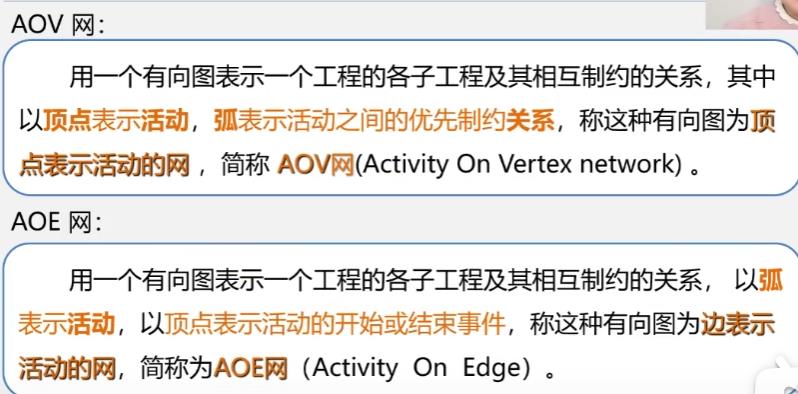
AOV网可解决拓扑排序问题
AOE网可解决关键路径问题
拓扑排序案例
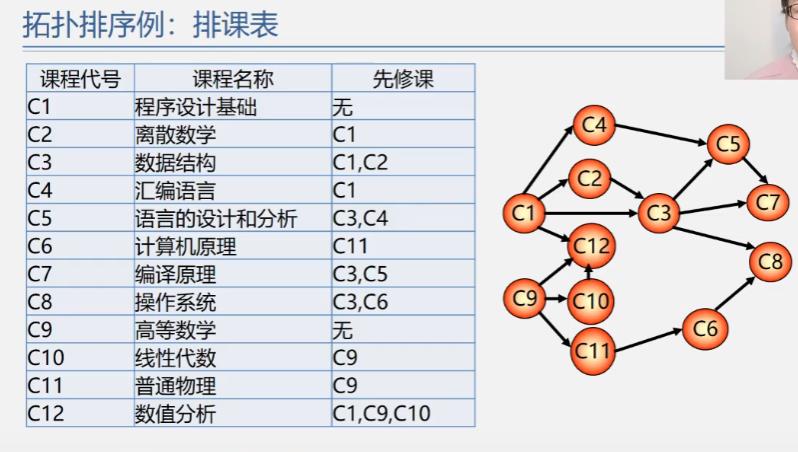
AOV网的特点
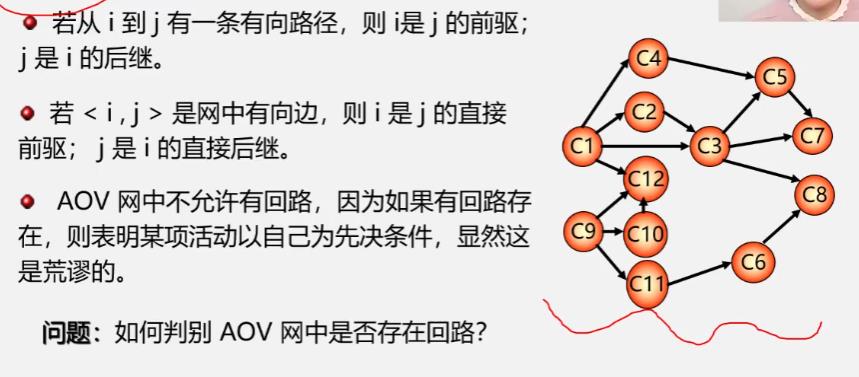
拓扑排序定义

拓扑排序方法
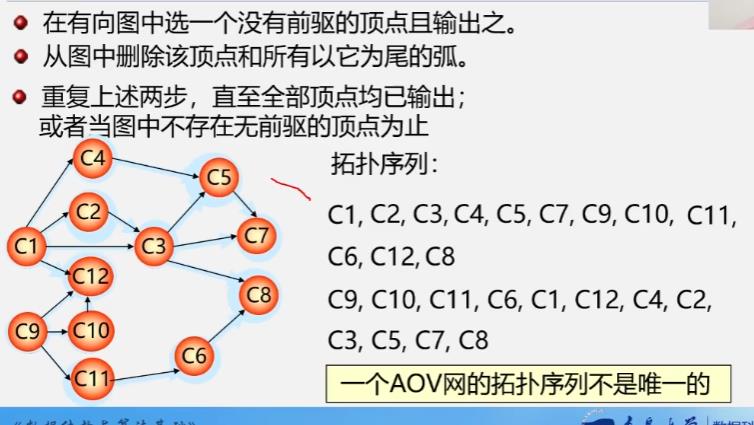
重要应用

4.关键路径
引例
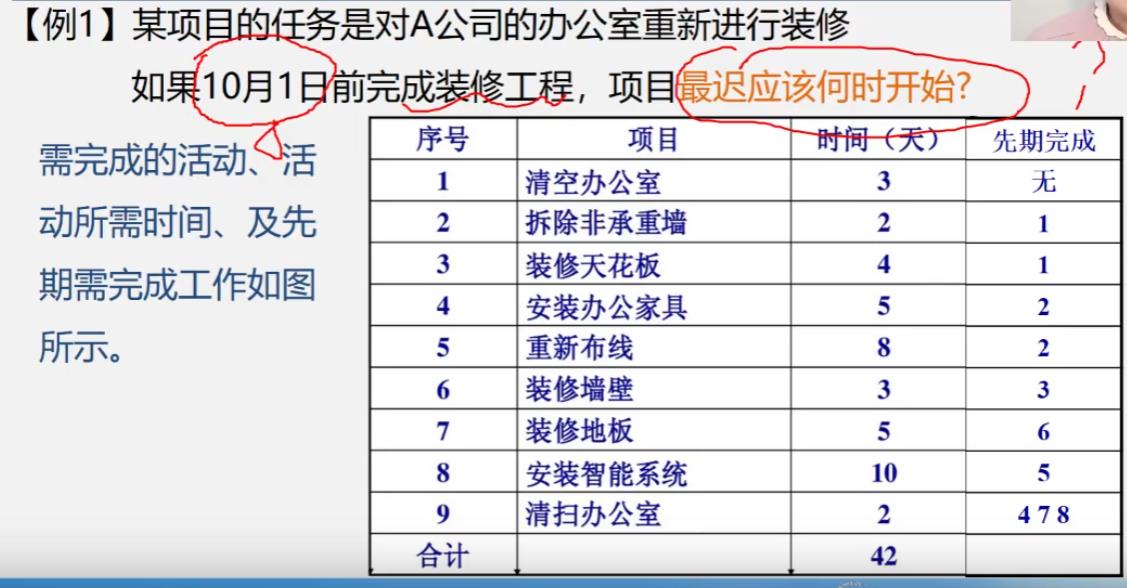
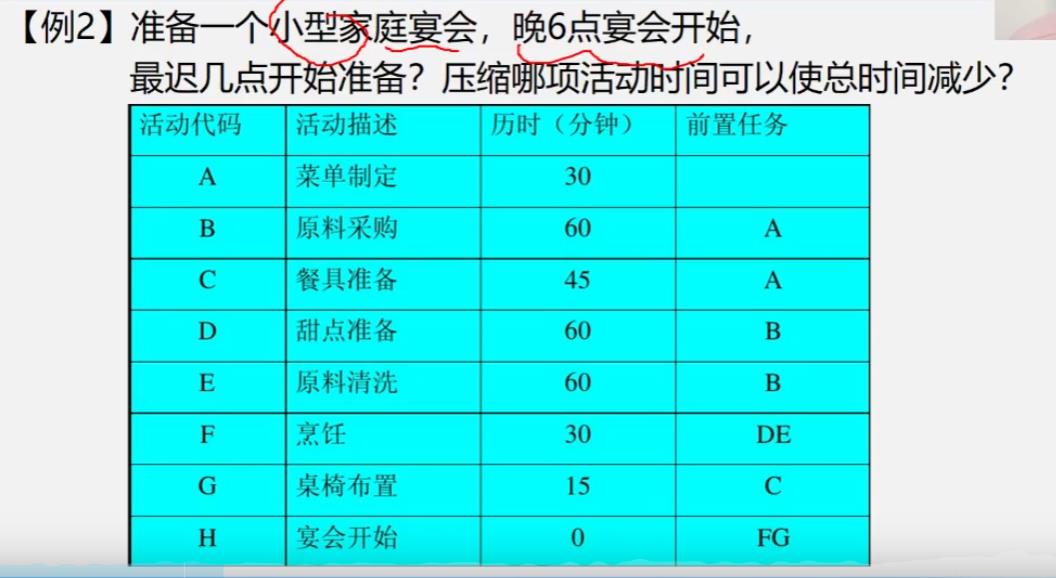
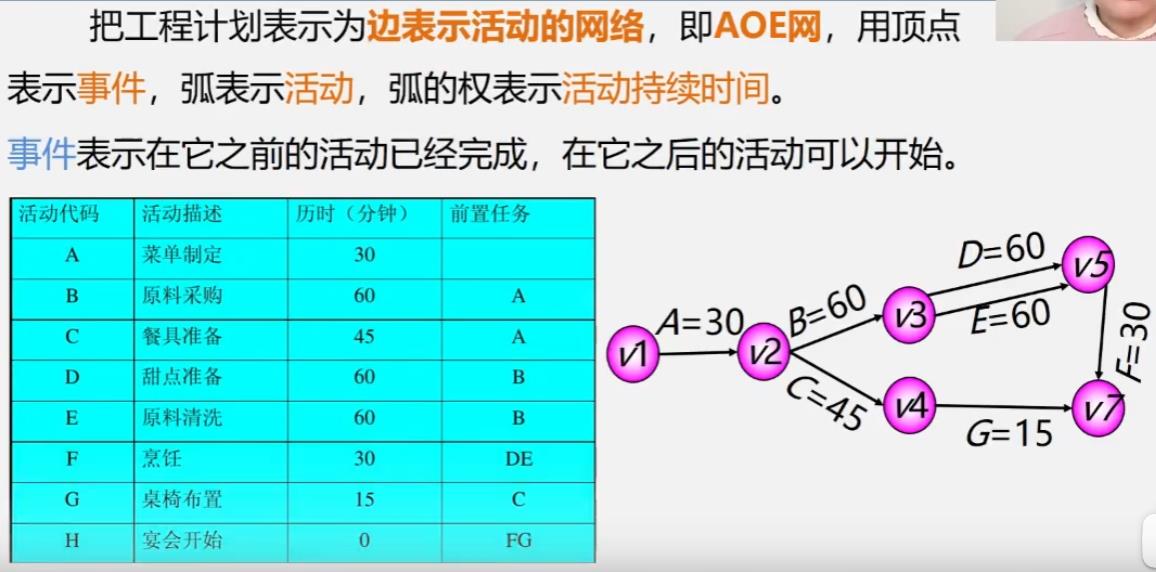
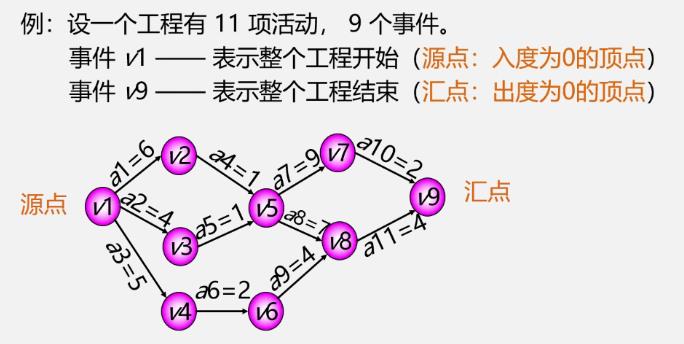
根据已知AOE网求解关键路径
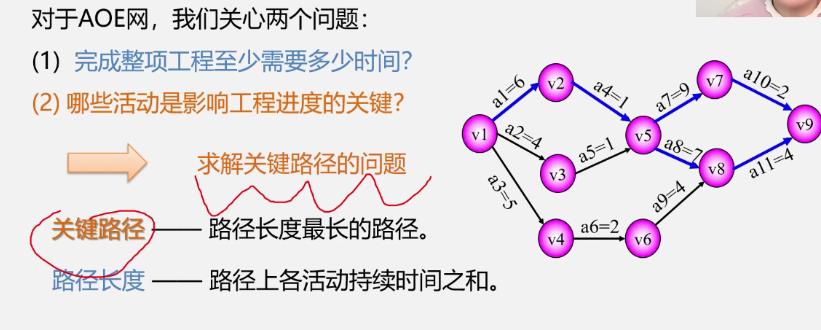
-
4个描述量
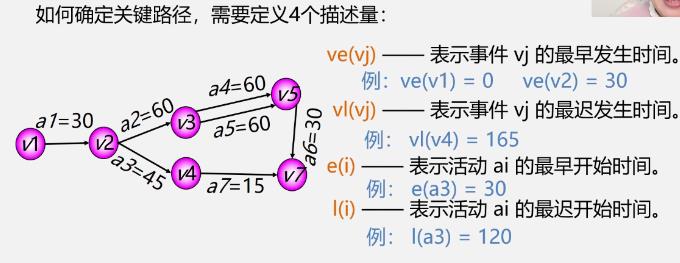

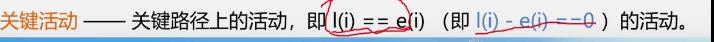
-
如何找关键活动?

-
如何求某一个顶点的最早发生时间和最晚发生时间

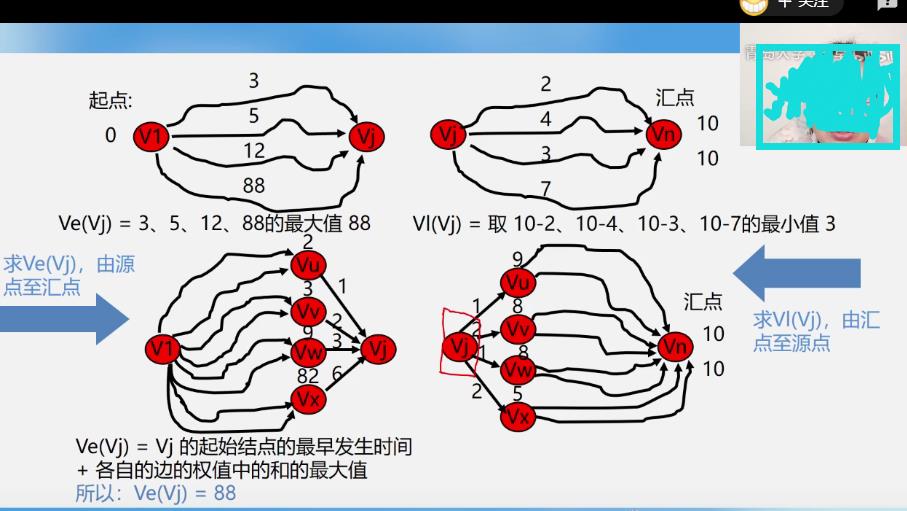
-
求关键路径步骤

-
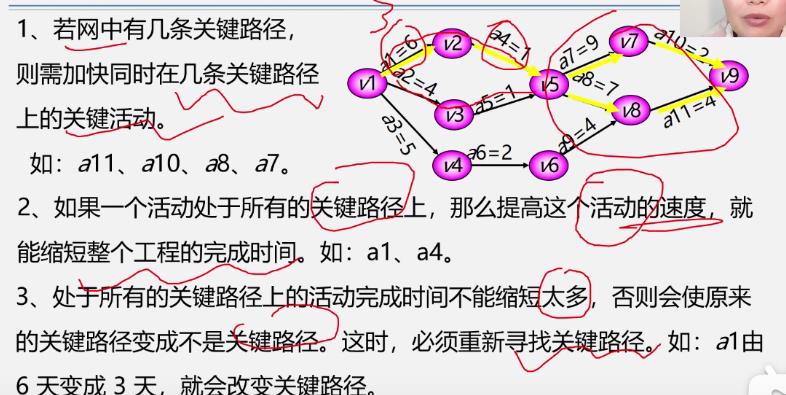
例

-
总结
以上是关于数据结构与算法学习笔记 图的主要内容,如果未能解决你的问题,请参考以下文章