拉格朗日 优美典范
Posted 飞凡可期
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了拉格朗日 优美典范相关的知识,希望对你有一定的参考价值。
%syms: good lagrange 朗格朗日好样的; %两种方式1:x=x0, eval(f1); 2:使用x,y,x,y subs替换函数,属性-值的花括号(元组对)即可;
syms x1 x2 x3 x4 x x5 x6
exp = (x-x2)*(x-x3)*(x-x4)/((x1-x2)*(x1-x3)*(x1-x4))
f1 = subs(exp, x,x1,x2,x3,x4,0,-2,-1,1,2)
f2 = subs(exp, x,x1,x2,x3,x4,0,-1,-2,1,2)
f3 = subs(exp, x,x1,x2,x3,x4,0,1,-2,-1,2)
f4 = subs(exp, x,x1,x2,x3,x4,0,2,-2,-1,1)
% changed to 1~4
f1 = subs(exp, x,x1,x2,x3,x4,3,1,2,4,5)
f2 = subs(exp, x,x1,x2,x3,x4,3,2,1,4,5)
f3 = subs(exp, x,x1,x2,x3,x4,3,4,1,2,5)
f4 = subs(exp, x,x1,x2,x3,x4,3,5,1,2,4)
% gap2
f1 = subs(exp, x,x1,x2,x3,x4,0,-4,-2,2,4)
f2 = subs(exp, x,x1,x2,x3,x4,0,-2,-4,2,4)
f3 = subs(exp, x,x1,x2,x3,x4,0,2,-4,-2,4)
f4 = subs(exp, x,x1,x2,x3,x4,0,4,-4,-2,2)
%middle gap 2 - 0;
f1 = subs(exp, x,x1,x2,x3,x4,0,-3,-2,2,3)
f2 = subs(exp, x,x1,x2,x3,x4,0,-2,-3,2,3)
f3 = subs(exp, x,x1,x2,x3,x4,0,2,-3,-2,3)
f4 = subs(exp, x,x1,x2,x3,x4,0,3,-3,-2,2)
%middle gap 2 - -1;
f1 = subs(exp, x,x1,x2,x3,x4,-1,-3,-2,2,3)
f2 = subs(exp, x,x1,x2,x3,x4,-1,-2,-3,2,3)
f3 = subs(exp, x,x1,x2,x3,x4,-1,2,-3,-2,3)
f4 = subs(exp, x,x1,x2,x3,x4,-1,3,-3,-2,2)
%middle gap 3 - 0;
f1 = subs(exp, x,x1,x2,x3,x4,0,-4,-3,3,4)
f2 = subs(exp, x,x1,x2,x3,x4,0,-3,-4,3,4)
f3 = subs(exp, x,x1,x2,x3,x4,0,3,-4,-3,4)
f4 = subs(exp, x,x1,x2,x3,x4,0,4,-4,-3,3)
!](https://img-blog.csdnimg.cn/7ef9263085a9445b8a09c0ce87db642f.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA6aOe5Yeh5Y-v5pyf,size_20,color_FFFFFF,t_70,g_se,x_16)
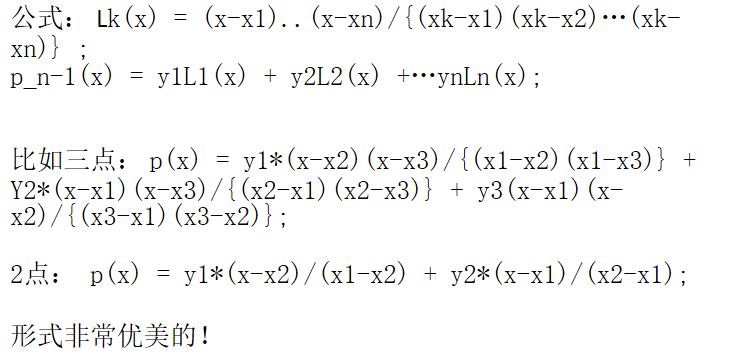
以上是关于拉格朗日 优美典范的主要内容,如果未能解决你的问题,请参考以下文章