❤️独家挑战全网最通俗易懂的神经网络的表达能力解释

Posted 2022-12-01 Super__Tiger

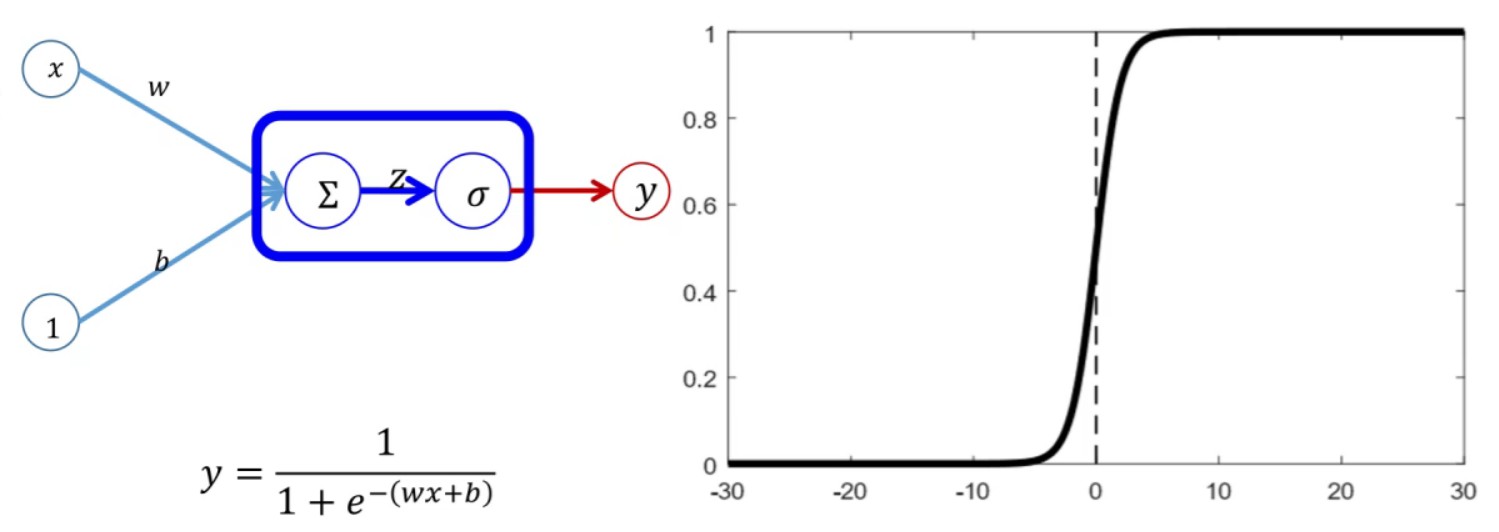
如上图所示，是初学者对于神经网络非线性表达能力最直观的印象图，输入为：x和1，激活函数为：$\mathbf{y}=\frac{1}{1+{\mathbf{e}}^{-\left(\mathbf{w}\mathbf{x}+\mathbf{b}\right)}}$，然后输出为：y；而右图则是sigmoid函数的函数图像。

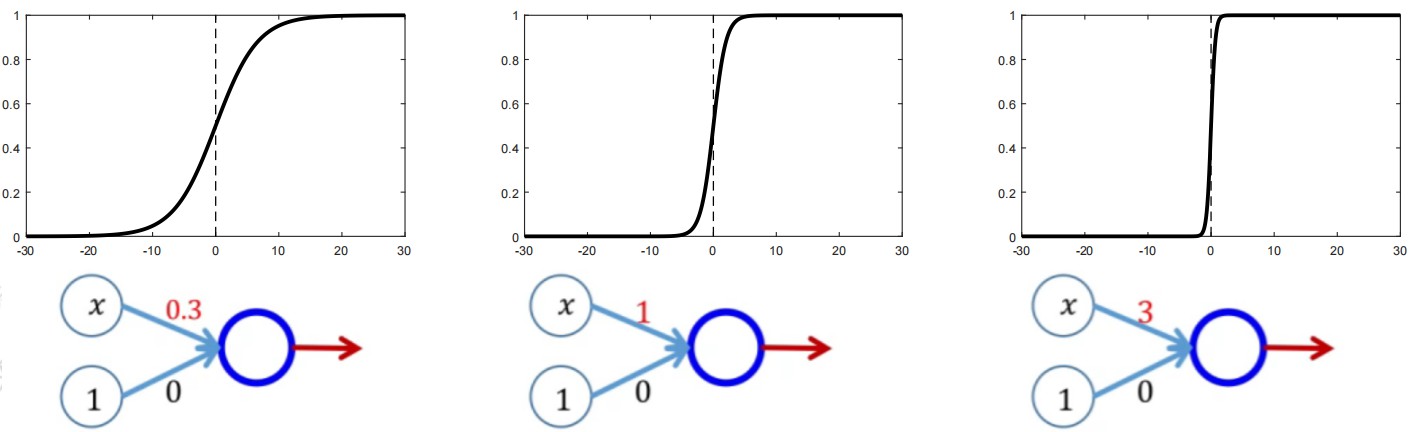
参见上图，让我们一步步来分析权重w对于输出函数y的影响：

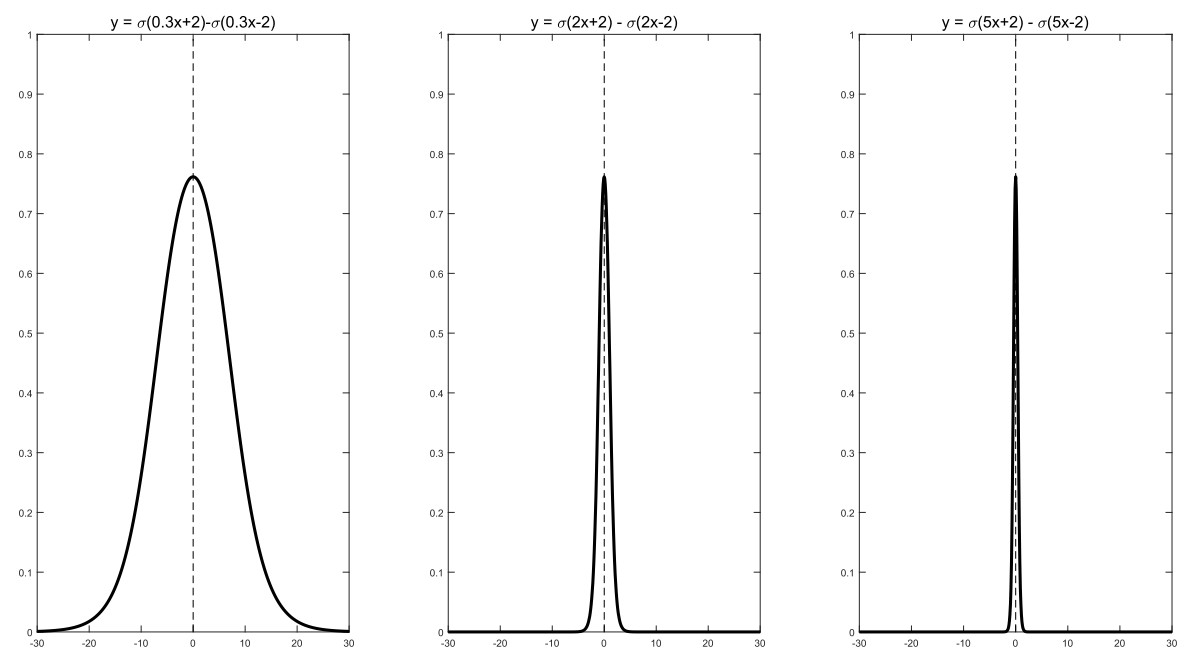
• 如果我们令b=0，并且我们的权重w取值为0.3，则我们的输出$\mathbf{y}=\frac{1}{1+{\mathbf{e}}^{-0.3\mathbf{x}}}$，此时的输出函数y明显坡度变得更加“平缓”。
• 如果我们令b=0，并且我们的权重w取值为3，则我们的输出$\mathbf{y}=\frac{1}{1+{\mathbf{e}}^{3\mathbf{x}}}$，此时的输出函数y明显坡度变得更加“陡峭”。
• 但是，x=0，y=0.5的分界位置却未发生任何改变，由此，我们得到一个结论：在b=0的情况下，我们通过改变权重参数w能够改变输出函数y的“陡峭”或者“平缓”的速度。

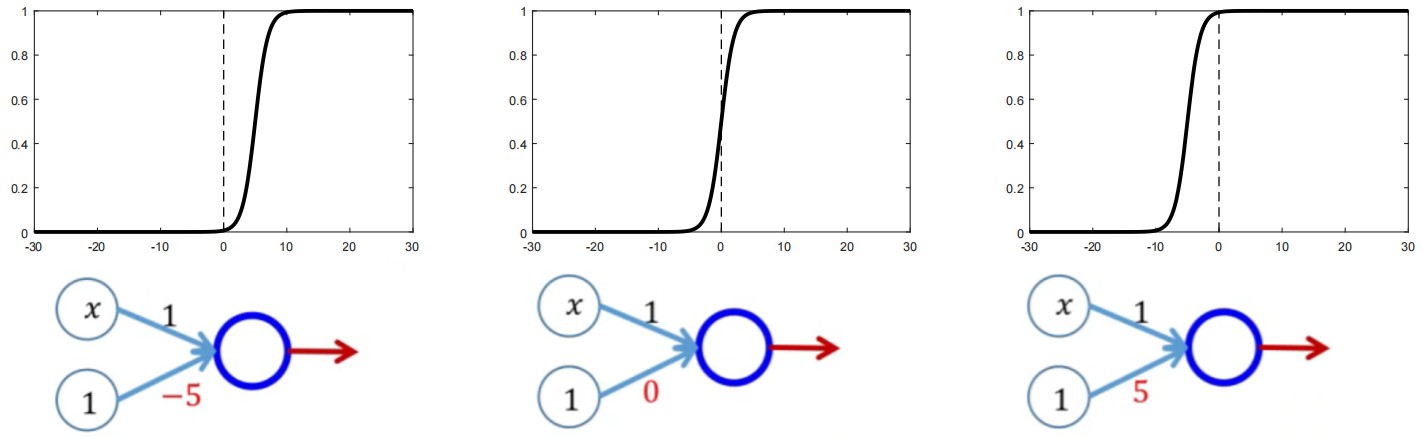
此时，我们会疑惑，那么如果权重w不变，仅改变偏置项b，会发生什么呢？参见上图，分析偏置项b对于输出函数y的影响：

• 如果我们令w=1，并且我们的偏置项b取值为-5，则我们的输出$\mathbf{y}=\frac{1}{1+{\mathbf{e}}^{-\left(\mathbf{x}-5\right)}}$，此时的输出函数y=0.5的分界位置向右发生了移动。
• 如果我们令w=1，并且我们的偏置项b取值为5，则我们的输出$\mathbf{y}=\frac{1}{1+{\mathbf{e}}^{-\left(\mathbf{x}+5\right)}}$，此时的输出函数y=0.5的分界位置向左发生了移动。
• 但是，输出函数y的坡度却未发生任何变化，由此，我们得到一个结论：在w=1的情况下，我们通过改变偏置项b能够改变输出函数y=0.5的分界位置。

综上所述，我们得到了w和b对输出函数y影响关系的终极奥义o(▼皿▼メ;)o！

• 改变权重参数w，即改变输出函数y的坡度（“平缓”/“陡峭”）；改变偏置项b，即改变输出函数y=0.5的分界位置。
• 如果通过改变权重参数w和偏置项b，那么我们的输出函数y就在x-y函数空间内“移动”了起来！

上面分析的是一个最初级神经网络的非线性拟合变化情况，那么如果两个及多个这样的初级神经元结构会是什么样子呢？

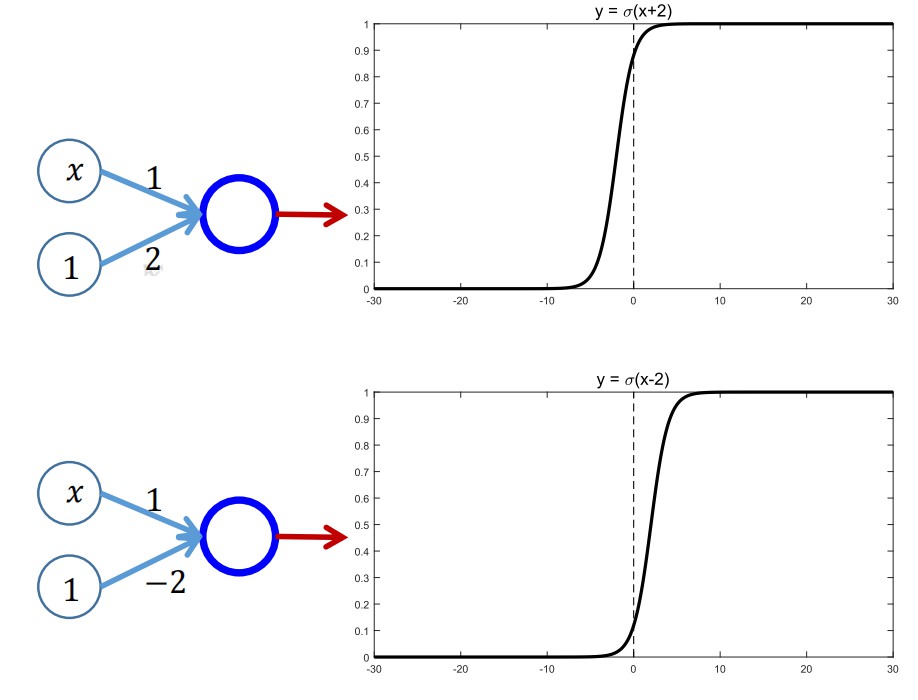
这里，我们给出了两个初级神经网络输入层结构的图示以及它们的输出函数图像：

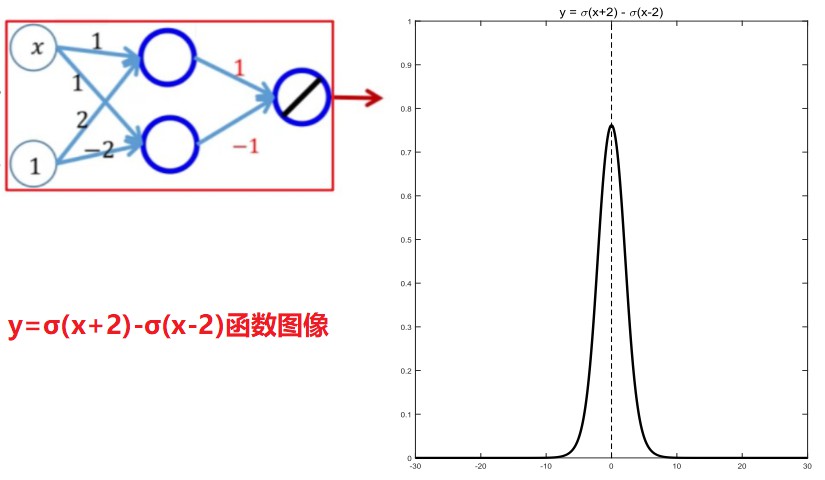
那么问题来了，它们复合成多层更加复杂的神经网络结构会是什么样子呢？

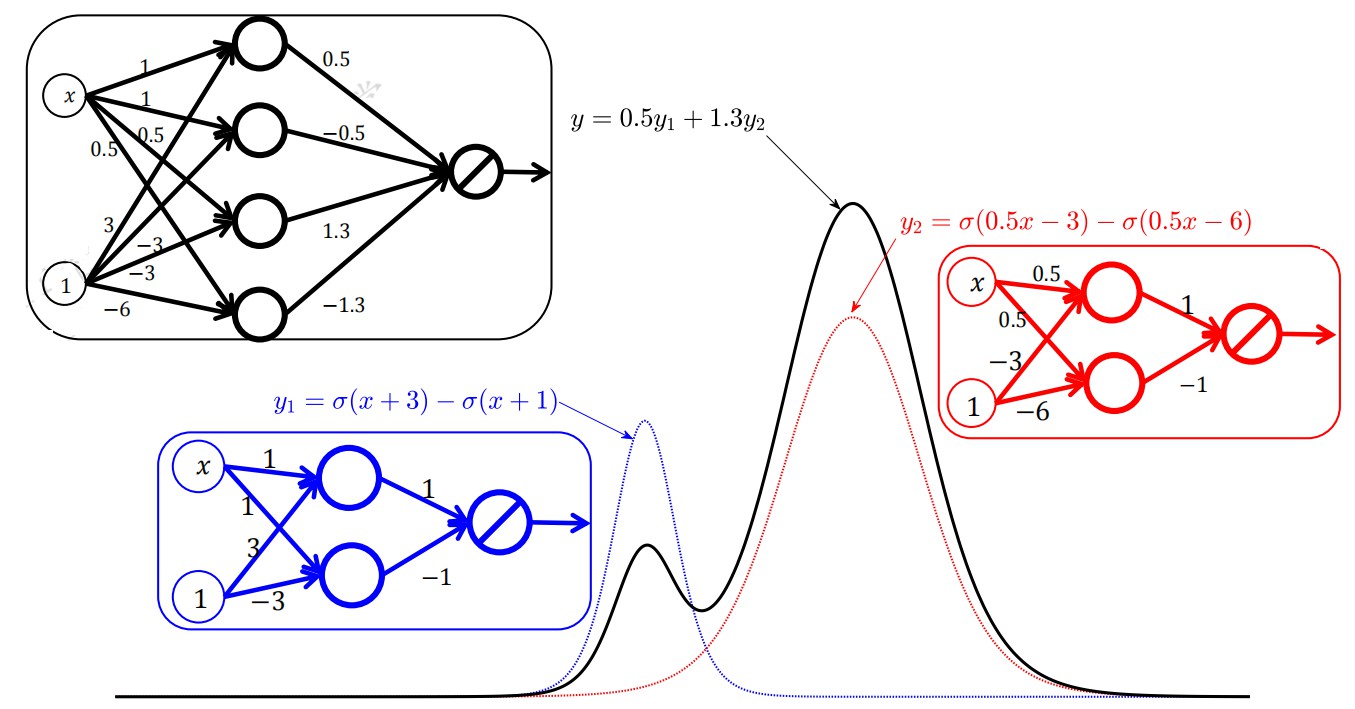
此时，我们能够看到上面黑色的曲线，已经复合成了一个比较复杂的函数图像，那么它对应的表达能力来说，也是更强的，当我们的网络结构足够复杂的时候，我们的函数图像将会迎来它的表达能力的“巅峰”，如下图所示。

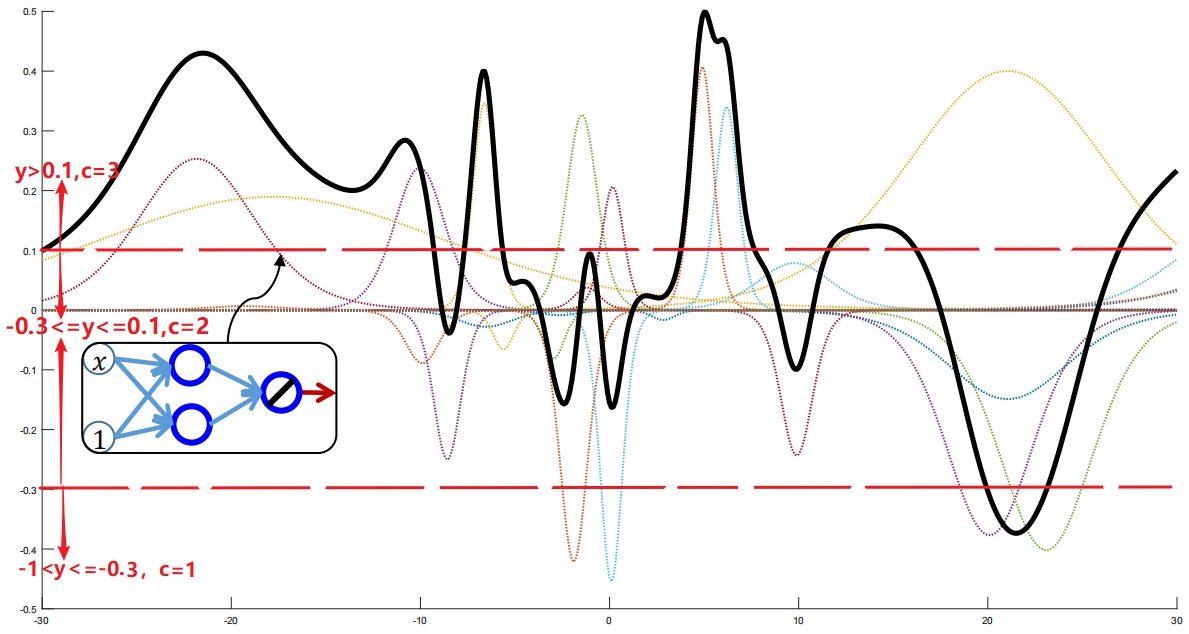
• 假如我们采用阈值分类的方法，则输入x，我们会得到以下情况：

  -1<y=φ(x)<=-0.3，则x的分类结果为c=1。

  -0.3<y=φ(x)<=0.1，则x的分类结果为c=2。

  y=φ(x)>0.1，则x的分类结果为c=3。

• 或者sigmoid这种分类方法的话，根据设定阈值分类即可。

• 如果采用softmax也是同理，只需要针对其中某一个类别对应神经元的输出，计算出${\mathbf{y}}_{\mathbf{j}}=\frac{\phi \left({\mathbf{x}}_{\mathbf{j}}\right)}{{\sum }_{\mathbf{j}=1}\phi \left({\mathbf{x}}_{\mathbf{j}}\right)}$，然后根据排序或者设定阈值分类即可。