盘点表示学习(Representation Learning)发展中的逻辑

Posted 2022-11-30 SoaringPigeon

Logic in Representation Learning

• 基于负例的对比学习：
• • 【以SimCLR为例】
  • Batch之外【以MocoV2为例】
• 基于对比聚类的对比学习：负例隐身术【以SwAV为例】
• 基于非对称网络结构的对比学习：模型不坍塌之谜【以BYOL和SimSiam为例】
• 基于冗余消除损失函数的对比学习：越简单越快乐【以Barlow Twins为例】

对比学习(Contrastive Learning) 是判别式自监督学习的一种，不依赖标注数据，要从无标注图像中自己学习知识。通过自动构造相似实例和不相似实例，要求习得一个表示学习模型，通过这个模型，使得相似的实例在投影空间中比较接近，而不相似的实例在投影空间中距离比较远。而如何构造相似实例，以及不相似实例，如何构造能够遵循上述指导原则的表示学习模型结构，以及如何防止模型坍塌(Model Collapse)，这几个点是其中的关键。目前 对比学习(Contrastive Learning) 的经典模型有Moco系列、SimCLR系列、BYOL、SwAV、DeepCluster系列、Barlow Twins等。

从防止模型坍塌的不同方法角度，我们可大致把现有方法划分为：

• 基于负例的对比学习方法
• 基于对比聚类的方法
• 基于非对称网络结构的方法
• 基于冗余消除损失函数的方法

其实我觉得防止模型坍塌还有种是通过有监督Loss约束，但这样就不是纯粹的对比学习，将成为半监督学习的方法，可以参考MeanTeacher、SE-SSD等文章如何防止模型坍塌(Model Collapse)。

基于负例的对比学习：

【以SimCLR为例】

对比学习是自监督学习，我们没有标注数据，所以需要如下图所示，自己构造相似数据（正例）以及不相似数据（负例）
对于某张图片，我们从可能的增强操作集合$T$中，随机抽取两种：$t_1\sim T$ 及 $t_2\sim T$ ，分别作用在原始图像上，形成两张经过增强的新图像$<x_1,x_2>$，两者互为正例。训练时，Batch内任意其它图像，都可做为$x_1$或$x_2$的负例。

有了正例和负例，接下来需要做的是：构造一个表示学习系统，通过它将训练数据投影到某个表示空间内，并采取一定的方法，使得正例距离能够比较近，负例距离比较远。

$Aug1$首先经过特征编码器Encoder(2D卷积) $f_{\theta }$ 转换成对应的特征表示 $h_i$ ，然后经过非线性变换结构Projector(两层MLP) $g_{\theta }$，进一步将特征表示 $h_i$ 映射成另外一个空间里的向量 $z_i$。同样地，$Aug2$ 经过同样Encoder和Projector映射成 $z_j$。

在表示空间 $Z$ 内，我们希望正例距离较近，负例距离较远。如果希望达成这一点，一般通过定义合适的损失函数来实现。在介绍损失函数前，我们首先需要一个度量函数，以判断两个向量在投影空间里的距离远近，一般采用对表示向量 $L_2$ 正则后的点积 或者表示向量间的 Cosine相似性 $S(z_i,z_j)=\frac{z_i^T{z}_j}{]]z_i]{]}_2]]z_j]{]}_2}$ 来作为距离度量标准。
SimCLR的损失函数采用InfoNCE Loss $$L_i=-log(\frac{exp(\frac{S(z_i,z_i^{+})}{\tau })}{{\sum }_{(j=0)}^{K}exp(\frac{S(z_i,z_j)}{\tau })})$$
其中，$<z_i,z_i^{+}>$代表两个正例相应的表示向量；负例个数K是一个超参，K数值可以根据需要调整大小；温度超参$\tau$一般设置0.1或者0.2，它将模型训练聚焦到有难度的负例，并对它们做相应的惩罚，难度越大，也即是与 $x_i$ 距离越近，则分配到的惩罚越多。$\tau$越小，模型学到的一致性信息就越少，多样性信息就越多，我们需要在一致性和多样性之间寻求一种平衡

这会引发一个问题：为什么这种投影操作，要做两次非线性变换，而不是直接在Encoder后，只经过一次变换即可呢？
实验证明，加上这个Projector对于提升模型效果改进很明显，这从经验角度说明两次投影变换是必须的。个人猜测，在接近任务的高层网络，也就是Projector，会编码更多跟对比学习任务相关的信息，低层就是Encoder，会编码更多跟任务无关的通用细节信息。对于下游任务，这种对比学习训练任务相关的高层特征，可能会带来负面影响。如果映射网络只包含Encoder的话，那么特征表示里会有很多预训练任务相关特征，会影响下游任务效果；而加上Projector，等于增加了网络层深，这些任务相关特征就聚集在Projector，此时Encoder则不再包含预训练任务相关特征，只包含更通用的细节特征，这样训练好的Encoder作为下游任务的预训练模型效果会更好。

Contribution:

• 证明了复合图像增强很重要
• 在Moco的Encoder结构后添加这个Projector结构并实验证明很有效

在此之后的对比学习模型，基本都采取了Encoder+Projector的两次映射结构，以及复合图像增强方法。

Batch之外【以MocoV2为例】

很多实验证明了：在基于负例的对比学习中，负例数量越多，对比学习模型效果越好，其实本质上，是因为越多负例，会包含更多的Hard负例，而这些Hard负例对于模型贡献较大，而easy负例，其实没多少贡献。因此一个自然的想法诞生了：不再局限于Batch内寻找负例 。

Moco V2是在整个训练集合内选择负例的典型方法，其实这个做法主要是Moco 提出的，Moco V2是吸收了SimCLR的Projector结构，以及更具难度的图像增强方法之后，针对Moco 的改进版本。

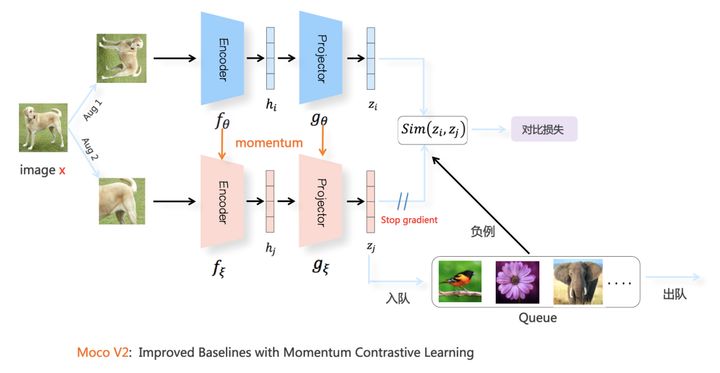
Contribution:

• 不再局限于Batch内寻找负例
• 下分支采用动量更新(Momentum Update)机制，而非SimCLR中的参数共享

下分枝的 动量更新(Momentum Update) 模型结构有两个作用：一个是将第二组图像增强视图 $Aug2$ 里的图像，映射到对应的表示空间编码 $z_j$ ，为第一组图像增强视图 $Aug1$ 提供正例；第二个作用是更新负例队列里数据的图像表示编码：一般会将最新Batch里Aug2对应的特征表示编码放入队列，而最老的那个Batch对应的图像编码出队，这样就可以不断更新负例队列内负例编码内容。

新问题来了:为什么负例队列里的图像编码，不用上分枝对应的最新的模型参数 $\theta$ ，而是采用缓慢移动的 $\xi$ 来更新呢？
下分枝的正例和负例参数缓慢而稳定的变动，才能提供较好的模型效果。这可能是因为缓慢更新的模型参数 $\xi$ ，给队列中来自不同Batch内的实例表征编码相对稳定而统一的改变，增加了表示空间的一致性。

基于对比聚类的对比学习：负例隐身术【以SwAV为例】

SwAV的模型结构如下图，其中的图像增强、Encoder以及Projector结构，与SimCLR基本保持一致。SwAV对 $Aug1$ 和 $Aug2$ 中的表示向量，根据Sinkhorn-Knopp算法[Reference:Sinkhorn算法]，在线对Batch内数据进行聚类。假设走下分枝的 $x_j$ 聚类到了 $q_j$ 类，则SwAV要求表示学习模型根据 $x_i$ 预测 $x_j$ 所在的类，也就是说，要将 $z_i$ 分到第 $q_j$类，具体损失函数采用 $z_i$ 和 $Prototype$ 中每个类中心向量的交叉熵： L a v g ( z i , q j ) = − ∑ k q j k ⋅ l o g ( p i k ) L_avg(z_i,q_j)=-\\sum_kq_j^k \\cdot log(p_i^k) Lavg​(zi​,q