数值分析中的样条函数:使用scipy.interpolate.splrep函数实现

Posted 2023-04-16

参考技术A

在 数学 学科 数值分析 中， 样条 是一种特殊的 函数 ，由 多项式 分段定义。样条的 英语 单词spline来源于可变形的样条工具，那是一种在 造船 和 工程制图 时用来画出光滑形状的工具。在中国大陆，早期曾经被称做“齿函数”。后来因为工程学术语中“放样”一词而得名。

在 插值 问题中，样条插值通常比 多项式插值 好用。用低阶的样条插值能产生和高阶的多项式插值类似的效果，并且可以避免被称为 龙格现象 的数值不稳定的出现。并且低阶的样条插值还具有“保凸”的重要性质。

在 计算机科学 的 计算机辅助设计 和 计算机图形学 中，样条通常是指分段定义的多项式 参数曲线 。由于样条构造简单，使用方便，拟合准确，并能近似 曲线拟合 和交互式曲线设计中复杂的形状，样条是这些领域中曲线的常用表示方法。

scipy.interpolate.splrep（x，y，w = None，xb = None，xe = None，k = 3，task = 0，s = None，t = None，full_output = 0，per = 0，quiet = 1 ）
找到一维曲线的B样条曲线表示。

给定数据点集，确定区间上度k的平滑样条近似。(x[i], y[i])xb <= x <= xe

x，y： array_like
定义曲线y = f（x）的数据点。

w： array_like，optional
权重的严格正秩1数组，其长度与x和y相同。权重用于计算加权最小二乘样条拟合。如果y值中的误差具有矢量d给出的标准偏差，则w应为1 / d。默认值为1（len（x））。

xb, xe：float, optional
适合的间隔。如果为None，则它们分别默认为x [0]和x [-1]。

k： int，optional
花键拟合的程度。建议使用三次样条。甚至应避免使用k值，尤其是在s值小的情况下。1 <= k <= 5

task：1, 0, -1, optional
如果task == 0，则在给定的平滑因子s下找到t和c。

如果task == 1，则找到t和c作为平滑因子s的另一个值。对于同一组数据，必须先前有一个task = 0或task = 1的调用（t将存储为内部使用）

如果task = -1，则找到给定结点t的加权最小二乘样条曲线。这些应该是内部结，因为两端的结将自动添加。

s：float, optional
平滑条件。满足以下条件来确定平滑度：sum（（w （y-g）） * 2，axis = 0）<= s其中g（x）是（x，y）的平滑插值。用户可以使用s来控制贴合度和贴合度之间的权衡。较大的s表示更平滑，而较小的s表示较不平滑。s的推荐值取决于权重w。如果权重代表y的标准偏差的倒数，则应在（m-sqrt（2 * m），m + sqrt（2 * m））范围内找到一个好的s值，其中m是x，y和w中的数据点。默认值：如果提供了权重，则s = m-sqrt（2 * m）。如果未提供权重，则s = 0.0（内插）。

t：array_like, optional
任务= -1所需的结。如果给出，则任务自动设置为-1。

f：full_outputbool, optional
如果非零，则返回可选输出。

per：bool, optional
如果非零，则将数据点视为周期为x [m-1]-x [0]的周期，然后返回平滑的周期样条近似。不使用y [m-1]和w [m-1]的值。

quiet：bool, optional
非零以禁止显示消息。不推荐使用此参数；请改用标准的Python警告过滤器。

Returns：
tck：tuple
元组（t，c，k），包含结向量，B样条系数和样条度。

fp：array, optional
样条近似值的平方残差的加权总和。

ier：int, optional
有关splrep成功的整数标志。如果ier <= 0，则表示成功。如果[1,2,3]中的ier发生错误，但未引发。否则会引发错误。

msg：str, optional
对应于整数标志ier的消息。

下面插值一个函数

样条之拉格朗日Lagrange(一元全区间)插值函数[转]

      这是使用拉格朗日插值函数生成的样条曲线。在数值分析中，拉格朗日插值法是以法国十八世纪数学家约瑟夫·拉格朗日命名的一种多项式插值方法。许多实际问题中都用函数来表示某种内在联系或规律，而不少函数都只能通过实验和观测来了解。如对实践中的某个物理量进行观测，在若干个不同的地方得到相应的观测值，拉格朗日插值法可以找到一个多项式，其恰好在各个观测的点取到观测到的值。这样的多项式称为拉格朗日（插值）多项式。数学上来说，拉格朗日插值法可以给出一个恰好穿过二维平面上若干个已知点的多项式函数。

关于插值与样条的介绍请看：http://www.cnblogs.com/WhyEngine/p/4020294.html

核心代码：

//////////////////////////////////////////////////////////////////////
// 一元全区间等距插值
//////////////////////////////////////////////////////////////////////
static float GetValueLagrange(const void* valuesPtr, int stride, int n, float t)
{ 
    int i,j,k,m;
    float z,s,xi,xj;
    float p,q;

    // 初值
    z = 0.0f;

    // 特例处理
    if (n < 1) 
    {
        return(z);
    }
    if (n == 1) 
    { 
        z = YfGetFloatValue(valuesPtr, stride, 0); 
        return(z);
    }
    if (n == 2)
    { 
        float y0 = YfGetFloatValue(valuesPtr, stride, 0); 
        float y1 = YfGetFloatValue(valuesPtr, stride, 1); 
        z = y0 + (y1 - y0)*t;
        return(z);
    }

    float xStep = 1.0f/(n - 1);

    // 开始插值
    if (t > 0.0f)
    { 
        p = t/xStep; 
        i = (int)p; 
        q = (float)i;

        if (p > q) 
        {
            i = i+1;
        }
    }
    else 
    {
        i = 0;
    }

    k = i-4;
    if (k < 0) 
    {
        k = 0;
    }

    m = i+3;
    if (m > n-1) 
    {
        m = n-1;
    }

    for (i = k; i <= m; i++)
    { 
        s = 1.0; 
        xi = i*xStep;

        for (j = k; j <= m; j++)
        {
            if (j != i)
            { 
                xj = j*xStep;
                // 拉格朗日插值公式
                s = s*(t-xj)/(xi-xj);
            }
        }

        z = z + s*YfGetFloatValue(valuesPtr, stride, i); 
    }

    return(z);
}

这是神一样的代码，反正我这辈子估计是看不懂了。

切图：

 

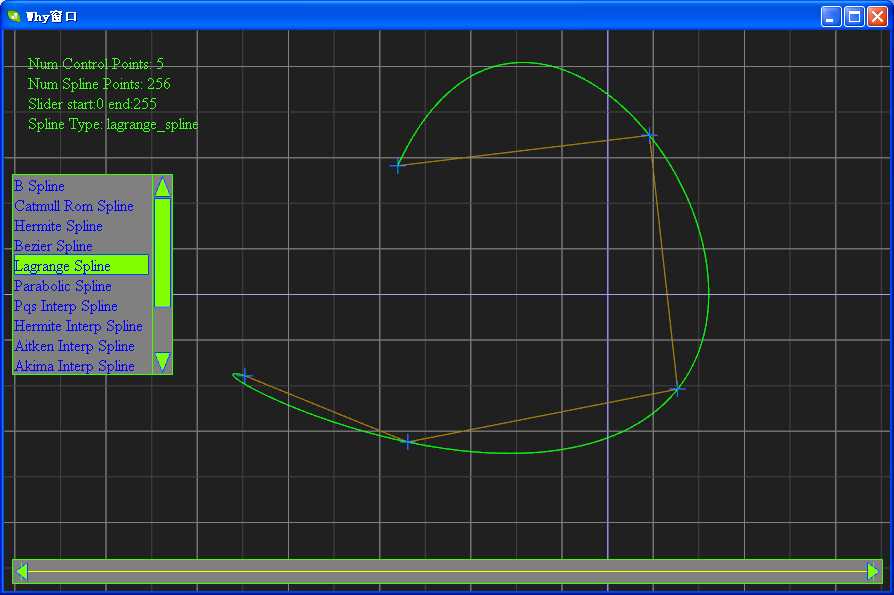
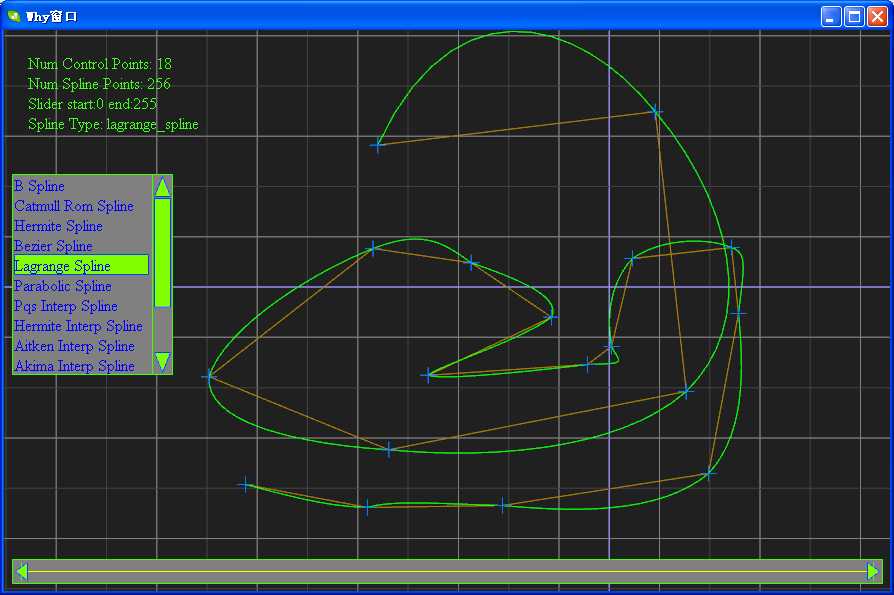
相关软件的下载地址为：http://files.cnblogs.com/WhyEngine/TestSpline.zip