最长公共子序列算法求破！杭电1159

Posted 2023-04-15

/*
输入s1和s2两个字符串比较他们相同子串的长度
用s2去匹配s1，将s1作为字典;
设i为[0,s2.length)区间中的某个值。
f(i)为含字母s2[i]的最大公共字串中的元素个数;
a[i]记录s2[i]字符在s1中出现的位子;
b[i]存放每次f(i)生成的长度;
f(i)=maxf(j)|0<=j<i AND s2[i]存在于s1(a[j]+1,s1.length-1)+1;
取出f(i)中的最大值就是我们要的结果
*/
#include<stdio.h>
#include<string.h>
char s1[600],s2[600];
int l1,l2;
int a[600],b[600];
int Max=0;
int f(int i)

int j,max=0,p=0,k;
if(strchr(s1,s2[i]))

for(j=0;j<l1;j++)

if(s2[i]==s1[j]) break;

p=j;
for(j=0;j<i;j++)

if(strchr(&s1[a[j]+1],s2[i])&&b[j]>max)

max=b[j];
for(k=a[j]+1;k<l1;k++)

if(s1[k]==s2[i])

p=k;
break;




b[i]=max+1;
if(b[i]>Max) Max=b[i];
a[i]=p;

else

a[i]=-1;
b[i]=0;


int main()

int i;
//freopen("input.txt","r",stdin);
while(scanf("%s %s",s1,s2)!=EOF)

Max=0;
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
l1=strlen(s1);//计算s1,s2的长度
l2=strlen(s2);
for(i=0;i<l2;i++)

f(i);

printf("%d\n",Max);

参考技术A 有标准的算法，采用动态规划 参考技术B 同上啊，是的

算法图解：动态规划之最长公共子串,最长公共子序列

首先介绍一下子串和子序列的不同。

子串必须要求是原来序列中连续的子序列。而子序列要求要低，可以删除中间一些元素，只要保持原来的顺序不变，删除中间元素即为子序列。

这里采用动态规划的方法计算两个字符串的最长公共子串和最长公共子序列。

最长公共子串：

查找公共子串时候，答案不一定在最后。

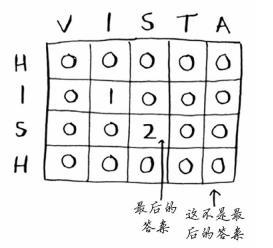
code:

a = 'awefawfishdsga'
b = 'foshdsqw'

graph = [[0 for i in range(len(a))] for j in range(len(b))]
max_value = 0
index = []

for i in range(len(graph)):
    for j in range(len(graph[0])):
        if i == 0 or j == 0:
            if(b[i] == a[j]):
                graph[i][j] = 1
        else:
            if(b[i] == a[j]):
                graph[i][j] = graph[i-1][j-1] + 1
        if(max_value < graph[i][j]):
            max_value = graph[i][j]
            index = [i,j]
print(max_value)
print(a[index[1]-max_value+1:index[1]]+a[index[1]])
最后保存了最大值和索引值，方便恢复最大公共子串。

最大公共子序列：

最大公共子序列不要求字符必须连续，只要顺序一样即可。所以，这里的填表算法稍微有变化。

效果如图：

这里唯一不同的就是当两个数字不相同的时候，最大子串是让其值为0，而最大子序列是让其值选择左边和上方两者最大值。

该算法解释起来是这样的：

对于两个字符串a,b。其最大字符子串为aim(a,b)。对于字符串a[:i+1],b[:j+1],他们的最大字符子序列为：

当a[i] == b[j] 时：aim(a[:i+1],b[:j+1]) + 1,

当a[i] ！= b[j] 时：aim(a[:i+1],b[:j)或者(a[:i],b[:j+1])，即两者之间取最大值即可。

这里就将问题分解为小问题。可以采用动态规划来解决。

code:

a = 'awefawfishdsga'
b = 'foshdsqw'

graph = [[0 for i in range(len(a))] for j in range(len(b))]
max_value = 0
index = []

for i in range(len(graph)):
    for j in range(len(graph[0])):
        if i == 0 and j == 0:
            if(b[i] == a[j]):
                graph[i][j] = 1
        elif i == 0 or j == 0:
            if(b[i] == a[j]):
                graph[i][j] = 1
            else:
                graph[i][j] = graph[i-1][j] if i-1>=0 else graph[i][j-1]
        else:
            if(b[i] == a[j]):
                graph[i][j] = graph[i-1][j-1]+1
            else:
                graph[i][j] = max(graph[i-1][j],graph[i][j-1])            
        if(max_value < graph[i][j]):
            max_value = graph[i][j]
            #index = [i,j]
print(max_value)

 同时：还有一个问题，这里找到了最大子序列，但是如何输出最大子序列呢？

这里采用回归的思想找最大子序列，首先再保存最大值的时候，将索引i,j保存。然后判断索引出两个字符串对于的字母是否相等，如果相等，则将字符添加在输出，如果不相等，判断graph中对应记录的最大子序列最大值和左边相等还是和上面相等，然后更新索引值即可。

code:

a = 'awefawfishdsga'
b = 'foshdsqw'

graph = [[0 for i in range(len(a))] for j in range(len(b))]
max_value = 0
index = []

for i in range(len(graph)):
    for j in range(len(graph[0])):
        if i == 0 and j == 0:
            if(b[i] == a[j]):
                graph[i][j] = 1
                index_str
        elif i == 0 or j == 0:
            if(b[i] == a[j]):
                graph[i][j] = 1
            else:
                graph[i][j] = graph[i-1][j] if i-1>=0 else graph[i][j-1]
        else:
            if(b[i] == a[j]):
                graph[i][j] = graph[i-1][j-1]+1
            else:
                graph[i][j] = max(graph[i-1][j],graph[i][j-1])            
        if(max_value < graph[i][j]):
            max_value = graph[i][j]
            index = [i,j]
i = index[0]
j = index[1]
if(max_value>0):
    str_max = []
    str_max.append(b[i])
    i -= 1
    j -= 1
    while i>=0 and j>=0:
        if b[i] == a[j]:
            str_max.append(b[i])
            i -= 1
            j -= 1
        else:
            if graph[i][j] == graph[i-1][j]:
                i -= 1
            else:
                j -= 1 
print(max_value)
print(''.join(str_max[::-1]))