二叉树三种遍历(先序，中序，后序)----超详细

Posted 2022-11-28 我是晓伍

目录

• 引入
• 先序遍历
• • 递归写法
  • 非递归写法
• 后序遍历
• • 非递归写法
• 中序遍历
• • 非递归写法
• 总结

引入

二叉树的遍历有许多种，例如深度优先搜索，广度优先搜索，在这里，我只介绍先序，中序，后序三种的递归与非递归遍历方法。

先序遍历

首先，先序遍历遵循，先访问根结点，再访问左子树，最后访问右子树的规律，如下图所示：


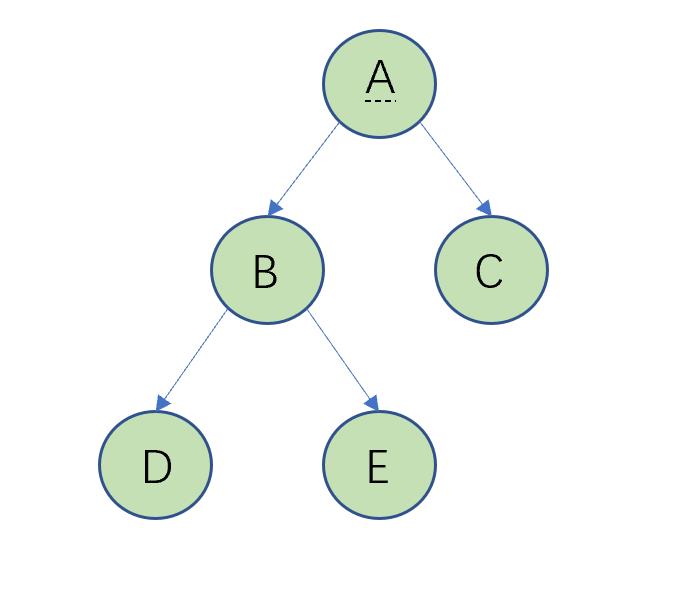
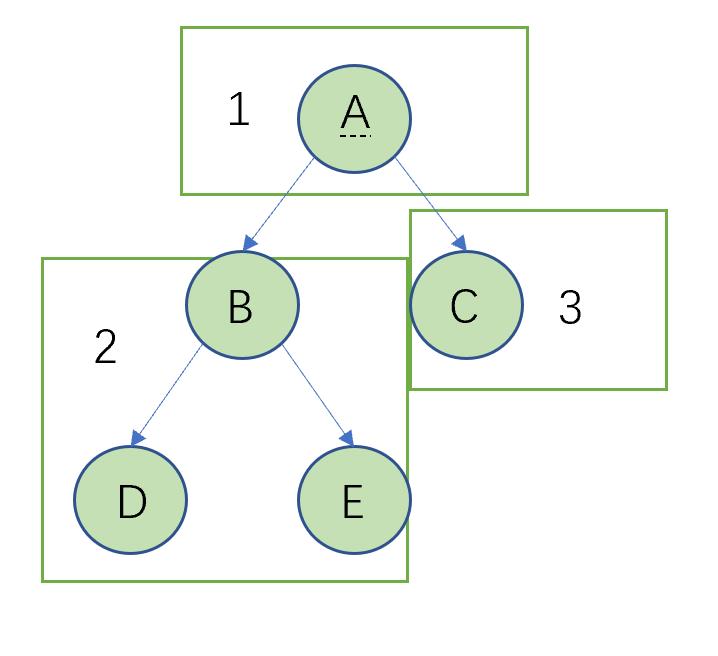
下面我们来模拟一下这个遍历的过程，首先访问到A，因为它是根节点，之后需要访问A的左子树，也就是上图中的2部分，在2中，先访问B，再访问B的左子树，在B的左子树中，先访问D，再访问D的左子树，D的左子树为NULL，之后访问D，的右子树NULL，到这里，B的左子树就访问完成了，这时候应该是要访问B的右子树,所以访问结点E，再访问结点E的左右子树，都为NULL，到这里，A的左子树被完全访问，之后去访问A的右子树，通过规律可知道访问的到是E。
综上，得到以前序遍历访问这颗树会得到：ABDEC

递归写法

根据先序遍历的定义，很容易写出一个递归函数：
首先明确递归函数的作用：根据先序遍历访问以root为根节点的二叉树
便可以写出以下代码：

//定义的二叉树
typedef struct BTNode

	TreeDataType val;
	struct BTNode* left;
	struct BTNode* right;
BTNode, * BiTree;
//先序遍历函数
void PrevOrder(BTNode* root)

之后再次进行分析，紧扣我们的定义
1.传入一个根节点，访问根节点，得到：

//定义的二叉树
typedef struct BTNode

	TreeDataType val;
	struct BTNode* left;
	struct BTNode* right;
BTNode, * BiTree;
//先序遍历函数
void PrevOrder(BTNode* root)

	printf("%c ", root->val);

2.通过先序遍历函数访问左子树得到：

//定义的二叉树
typedef struct BTNode

	TreeDataType val;
	struct BTNode* left;
	struct BTNode* right;
BTNode, * BiTree;
//先序遍历函数
void PrevOrder(BTNode* root)

	printf("%c ", root->val);
	PrevOrder(root->left);

3.通过先序遍历函数访问右子树得到：

//定义的二叉树
typedef struct BTNode

	TreeDataType val;
	struct BTNode* left;
	struct BTNode* right;
BTNode, * BiTree;
//先序遍历函数
void PrevOrder(BTNode* root)

	printf("%c ", root->val);
	PrevOrder(root->left);
	PrevOrder(root->right);

这之后考虑递归结束条件 – 当结点为空时结束

//定义的二叉树
typedef struct BTNode

	TreeDataType val;
	struct BTNode* left;
	struct BTNode* right;
BTNode, * BiTree;
//先序遍历函数
void PrevOrder(BTNode* root)

	if (root == NULL)
	
		return;
	
	
	printf("%c ", root->val);
	PrevOrder(root->left);
	PrevOrder(root->right);

这就是完整的递归版先序遍历代码了。

非递归写法

递归写法比较简单，难一点的写法是非递归的写法，实际上，递归就是隐形维护了一个栈，所以非递归写法就是使用栈来通过迭代实现先序遍历效果。

还是同样给一颗二叉树

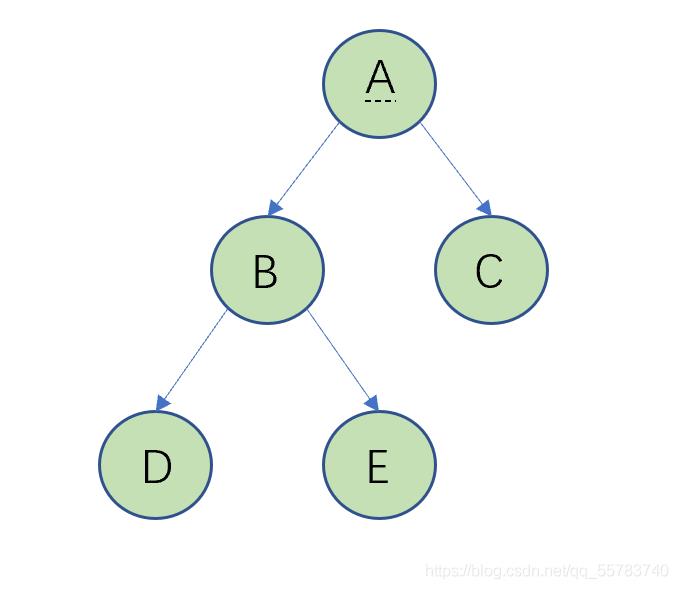
我们知道它的前序遍历结果是ABDEC,不妨通过这个结果来用栈推到出过程，第一个得到的结点是A，我们让A指针先进栈再出栈，之后让右指针进栈，左指针进栈，在这里有的同学可能会有疑惑，为什么不是先左再右呢？是因为栈是LIFO形式的，所以到时候会先出去。
现在栈中有C和B两个指针类似如图理解：

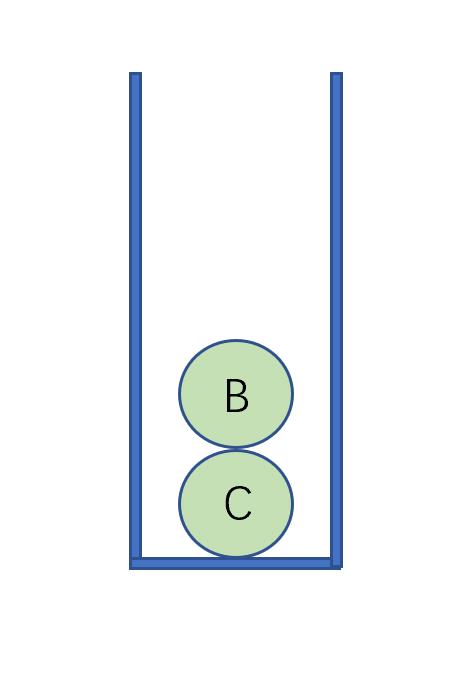
之后继续出栈，同样的把出栈结点指针对应的结点的右指针左指针分别进栈：

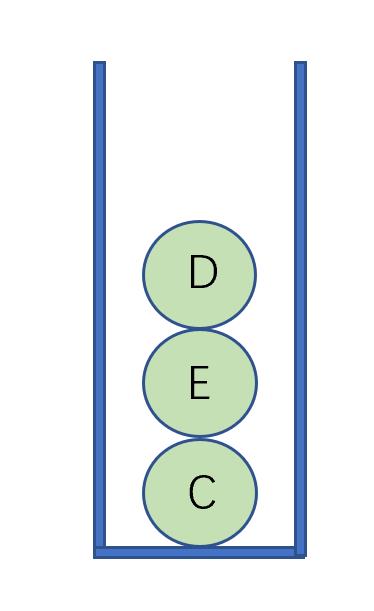
一直重复这个过程知道栈为空便得到非递归版本的先序遍历，代码如下：

TreeNodeType* PrevOrder(BTNode* root, int* size)

	if (root == NULL)
	
		return NULL;
	

	TreeNodeType* nums = (TreeNodeType*)malloc(sizeof(TreeNodeType) * 100);
	//初始化栈
	SqStack s;
	InitStack(&s);
	//将第一个节点压栈
	PushStack(&s, root);
	while (!EmptyStack(&s))
	
		//节点出栈
		BTNode* Node = PopStack(&s);
		nums[(*size)++] = Node->val;
		//压入右节点
		if (Node->right != NULL)
		
			PushStack(&s, Node->right);
		
		//压入左节点
		if (Node->left != NULL)
		
			PushStack(&s, Node->left);
		
	
	return nums;

由于三种递归写法都大同小异，之后的中序遍历和后序遍历的递归写法这里就不再赘述

后序遍历

非递归写法

这里我们先将后序遍历的非递归写法，因为后序遍历非递归写法和先序遍历有着高度统一的关系，后序遍历的顺序是是左子树，右子树，根节点，
我们只要把先序遍历的非递归写法中的入栈顺序调换一下：把先右节点指针压栈再左节点指针压栈改成先左再右，这样得到的顺序是，根节点，右子树，左子树，这之后只要逆序一下数组，就能得到左子树，右子树，根节点这个顺序。
代码如下：

//非递归后序遍历
TreeNodeType* PostOrder(BTNode* root, int* size)

	if (root == NULL)
	
		return NULL;
	
	TreeNodeType* nums = (TreeNodeType*)malloc(sizeof(TreeNodeType) * 100);
	//初始化栈
	SqStack s;
	InitStack(&s);
	//将第一个节点压栈
	PushStack(&s, root);
	while (!EmptyStack(&s))
	
		//节点出栈
		BTNode* Node = PopStack(&s);
		nums[(*size)++] = Node->val;
		//压入左节点
		if (Node->left != NULL)
		
			PushStack(&s, Node->left);
		
		//压入右节点
		if (Node->right != NULL)
		
			PushStack(&s, Node->right);
		
	

	//数组逆序
	int left = 0;
	int right = *size - 1;
	while (left < right)
	
		int temp = nums[left];
		nums[left] = nums[right];
		nums[right] = temp;
		left++;
		right--;
	

	return nums;

中序遍历

非递归写法

中序遍历和前面的有些不一样，首先我们肯定的是：第一个节点肯定是树最左边的节点，那么我们一路向左遍历，把每个节点压入栈中，如图所示：

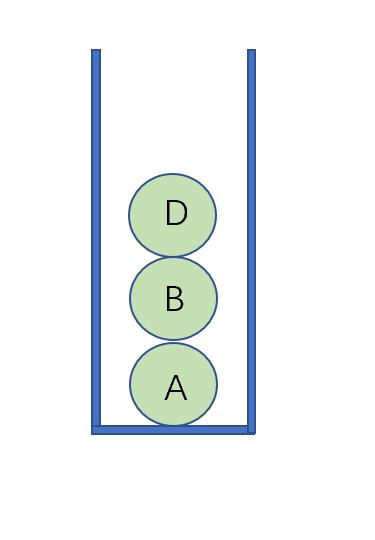
之后开始出栈，每次出一个节点指针，去访问它的右节点，如果存在，那么一直访问该右节点的左节点，每次将左节点压入栈中。
重复上述过程。

//非递归中序遍历
TreeNodeType* InOrder(BTNode* root, int* size)

	if (root == NULL)
	
		return NULL;
	

	TreeNodeType* nums = (TreeNodeType*)malloc(sizeof(TreeNodeType) * 100);
	SqStack s;
	InitStack(&s);
	BTNode* node = root;
	//当目前的node不为空或者栈不为空
	while (node || !EmptyStack(&s))
	
		//持续的将左节点压入栈中
		while (node)
		
			PushStack(&s, node);
			node = node->left;
		
		BTNode* element = PopStack(&s);
		//node = PopStack(&s);
		nums[(*size)++] = element->val;
		//出栈后访问右节点
		if (element->right != NULL)
		
			node = element->right;
		
	

	ret

在这里插入代码片

总结

三种遍历的递归版都大差不差，值得注意的是非递归版，思路的风格会不一样。