区块链与密码学第9-6讲：基于身份的群签名算法 I

Posted 2022-11-27 Dig Quant

【本课堂内容全部选编自PlatON首席密码学家、武汉大学国家网络安全学院教授、博士生导师何德彪教授的《区块链与密码学》授课讲义、教材及互联网，版权归属其原作者所有，如有侵权请立即与我们联系，我们将及时处理。】

9.6CZK03算法

基于ID的数字签名方案中，双线性的引入为验证签名和打开签名都提供方便，CZK03群签名方案的安全性在随机预言机模型下是可证明安全的，但是即使是获得群成员证书的群成员在产生每一个签名时都需要从群管理员处获得新的授权，效率非常低，也使得群管理员的速度成为限制整个系统的瓶颈。

Gap Diffie-Hellman群

令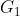是由生成元P产生的循环加法群，它的阶为素数q，假设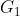中求逆和乘法是有效的，我们将以下问题引入

DLP：已知两个元素P和Q，找到一个整数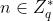，使得等式Q=nP成立

CDHP：已知P,aP,bP，其中a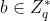，，计算abP

DDHP：已知P,aP,bP,cP，其中a,b,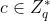,判断等式c≡ab mod q是否成立

如果DDHP可以在多项式时间内解出，但没有多项式时间算法可以在不可忽略的概率下解出CDHP或DLP，则我们称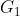为Gap Diffie-Hellman群。

下面介绍CZK03的算法流程：

1. Setup()

群管理员令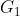为Gap Diffie-Hellman群，生成元为P且它的阶为素数q。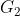为一个阶为素数q的乘法循环群，一个双线性对映射为e: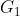×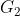→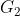。相关hash函数为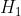：0,1*×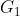→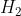；：0,1*×→

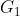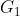
群管理员随机选择一个数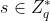，设置群管理员公钥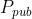=sP 群公钥为γ=,,e,q,P,P_pub ,,。

用户随机选择一个数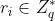，并将=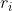P发送给群管理员。群管理员计算用户的部分私钥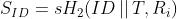并将它通过安全信道发送给用户。

2. Enroll()

 

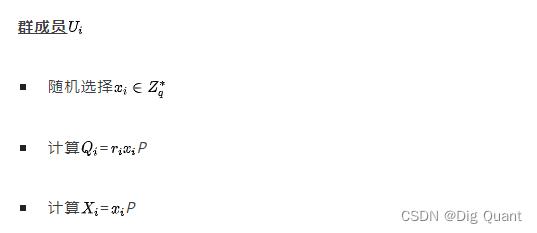
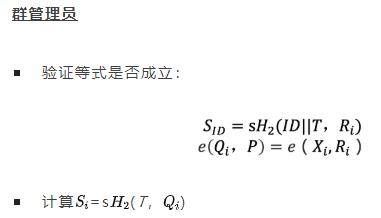
3. Sign()

4. Verify()

接收者

如果时间戳T是有效的，验证者计算：

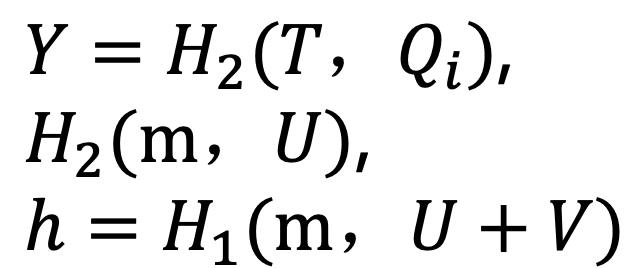
若以下等式成立，则验证者接受这个签名：

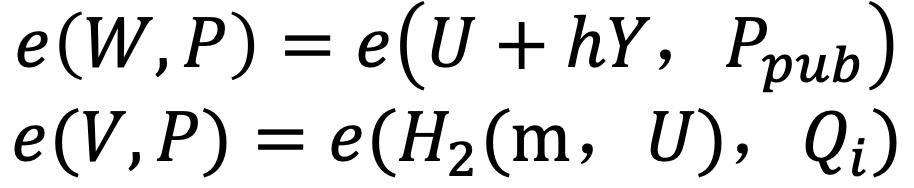
5. Open()

对于一个有效的群签名，群管理者能通过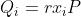轻松确定签名用户的身份。而且用户无法抵赖，这是因为群管理者能提供等式：

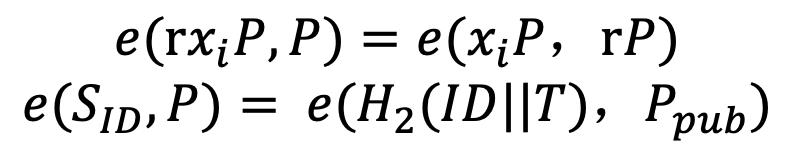
证明这个签名确实是用户签署的。

今天的课程就到这里啦，下节课我们将继续学习基于身份的群签名算法，敬请期待！

同学们可以关注点宽学园，每周持续更新区块链系列课程，小宽带你进入区块链世界。我们下节课见啦。

【区块链与密码学】课堂回顾：

区块链与密码学系列文章合集