线性不可分SVM 软间隔

Posted 2022-11-27 Zetaa

前言：仅个人小记。参看https://blog.csdn.net/qq_25847123/article/details/108058804。

线性不可分

大部分样本线性可分，总体线性不可分。

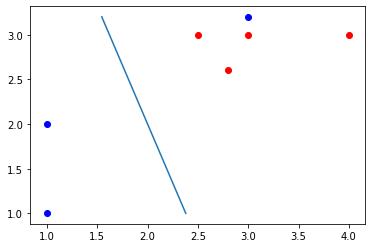
引入松弛变量

某些样本点不能满足函数间隔大于等于 $1$ 这个约束条件，软间隔策略就是对每个样本点引入一个松弛变量 $\xi \ge 0$。是的函数间隔加上松弛变量是大于等于 $1$ 的。此时，之前硬间隔最大化中的约束条件更变为
$$y_i(\mathbf{w}\cdot {\mathbf{x}}_i+b)\ge 1-{\xi }_i$$
同时，对每个松弛变量 ${\xi }_i$ 支付一个代价 ${\xi }_i$。目标函数更变为
$$\frac{1}{2}||w|{|}^2+C\sum _{i=1}^N{\xi }_i$$

$C$ 成为惩罚参数，取决于实际的应用场景。$C$ 值越大，则对误分类的惩罚越大，$C$ 值越小，对误分类的惩罚越小。现在，最小化目标函数意味着：1) 使得 $\frac{1}{2}||w|{|}^2$ 尽量小即间隔尽量大，同时使误分类点的个数尽量小，$C$ 是调和二者的系数。

线性不可分SVM的凸二次规划

线性不可分的线性支持向量机的学习问题更变为如下凸二次规划问题(原始问题)：
$$\begin{array}{c}\underset{\mathbf{w},b}{\max }\frac{1}{2}||w|{|}^2+C\sum _{i=1}^N{\xi }_i\\ \mathsf{s}.\mathsf{t}.y_i(\mathbf{w}{\mathbf{x}}_i+b)\ge 1-{\xi }_i,i=[1,N]\\ {\xi }_i\ge 0,i=1,2,...,N\end{array}$$

可以证明 ，$\mathbf{w}$的解是唯一的，而$b$可能不唯一，而是存在于一个区间（实际应用中，往往可以直接求出来）。

线性支持向量机的对偶形式

$$\begin{array}{c}\underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{i=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j({\mathbf{x}}_i{\mathbf{x}}_j)-\sum _{i=1}^N{\alpha }_i\\ \mathsf{s}.\mathsf{t}.\sum _{i=1}^N{\alpha }_i{y}_i=1\\ 0\le {\alpha }_i\le C,i=1,2,...,N\end{array}$$

进一步得到原问题的解，

$$\begin{array}{c}{w}^{\ast }=\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{\mathbf{x}}_i\\ b^{\ast }=y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i({\mathbf{x}}_i{\mathbf{x}}_j)\end{array}$$
其中，$j$是对应一个 α ∗ \\alpha^* α线性不可分SVM 软间隔

机器学习支持向量机（SVM）——软间隔线性不可分（理论+图解+公式推导）

SVM详解

SVM常考细节

SVM笔记四之线性支持向量机(软间隔最大化)

支持向量机（SVM）--软间隔