acm-icpc 有一道题（好像是World Final的），要求判断一个多项式是不是恒为整数，求这道题，急！

Posted 2023-04-13

如题
是判断一个整系数多项式是否恒为一个数的倍数
具体的说：设F(x)=a0+a1*x+a2*x^2+a3*x^3+……+an*x^n，问是否对于任意x∈N+，d|F(x)，其中d为常数。

设多项式次数为n，取n=0,1,2,3,...,n-1验证结果就行了，可以利用差分证明这是充要的追问

如果n比较大，不能逐个验证呢？

参考技术A 2l貌似正解。。。

2018 ACM-ICPC World Finals Gym-102482I Triangles

题目传送门

分析：
一道破题调一天。。。
小学数三角形题做不来，我被开除人籍了QAQ

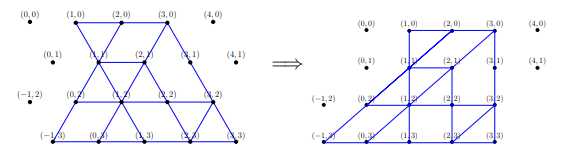
像这样处理一下（其实代码中可以不用这样处理，只是方便理解）
我们先想一下如何求这种形状(△)，向下的三角形类似处理就好了
我们可以边做边处理每个点向左，向上，向右上延伸的最长距离
每一行单独处理
一个点((x,y))右上延伸的距离(D)，说明这个点可以对区间[x+1,x+D]产生贡献，扫的时候树状数组上插入删除就好了
每个点为等腰直角三角形右下角时，假设它向上向左延伸距离较小值为(D)，能对它贡献的区间为[x-D,x]
树状数组单点修改区间查询
(O(n^{2}logn))还真跑得过2333

#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<vector>

#define maxn 6005
#define MOD 998244353

using namespace std;

inline int getint()
{
	int num=0,flag=1;char c;
	while((c=getchar())<‘0‘||c>‘9‘)if(c==‘-‘)flag=-1;
	while(c>=‘0‘&&c<=‘9‘)num=num*10+c-48,c=getchar();
	return num*flag;
}

int R,C;
char s[maxn][maxn<<1];
int A1[2][maxn<<1],A2[2][maxn<<1];
int T[maxn<<1];
vector<int>V[maxn<<1];
inline void update(int x,int num)
{for(int i=x;i<=C;i+=i&(-i))T[i]+=num;}
inline int getans(int x)
{int num=0;for(int i=x;i>0;i-=i&(-i))num+=T[i];return num;}
long long ans;


inline void solve()
{
	int now=1,pre=0;
	memset(A1,0,sizeof A1),memset(A2,0,sizeof A2);
	for(int t=3;t<=R;t+=2,swap(now,pre))
	{
		memset(T,0,sizeof T),memset(A1[now],0,sizeof A1[now]),memset(A2[now],0,sizeof A2[now]);
		int L=0;
		for(int i=1;i<=C;i++)if(s[t][i]==‘x‘)
		{
			if(i>2&&(s[t-1][i-1]==92||s[t-1][i-1]==47))A1[now][i]=A1[pre][i-2]+1;
			else A1[now][i]=0;
			if(i<C&&(s[t-1][i+1]==92||s[t-1][i+1]==47))A2[now][i]=A2[pre][i+2]+1;
			else A2[now][i]=0;
			
			if(s[t][i-1]==‘-‘)L++;
			else L=0;
			int tmp=min(L,A1[now][i]);
			if(tmp)ans+=getans(i)-getans(i-tmp*4-1);
			
			for(int j=0;j<V[i].size();j++)update(V[i][j],-1);
			V[i].clear();
			if(A2[now][i])
			{
				update(i,1);
				if(i+A2[now][i]*4<=C)V[i+A2[now][i]*4].push_back(i);
			}
		}
	}
}

int main()
{
	R=getint()*2-1,C=getint()*2;
	for(int i=1;i<=R;i++)gets(s[i]+1);
	solve();
	reverse(s+1,s+R+1);
	solve();
	printf("%lld
",ans);
}