运筹学最大流问题?
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了运筹学最大流问题?相关的知识,希望对你有一定的参考价值。
这个地方为什么是14啊

按三个原则
发点发出的总流量等于收点收到的总流量。
每一个中间点进去的总流量等于出去的总流量。
流量小于等于容量
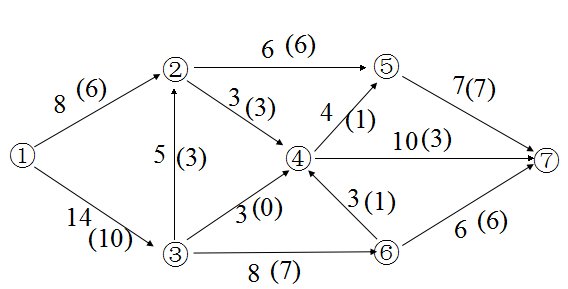
比如上面这个图,括号中给出的是初始流量。
V1发出6+10=16,V7收到7+3+6=16
V2收到6+3=9,发出6+3=9
V3收到10,发出3+0+7=10
V4/V5/V6亦是如此
你的图我看得有点模糊,你自己做一下即可。


老师,就是这个最大流14是怎么得来的我想不通
我都晓得留的路线了
参考技术A 最短路问题一般建立在 赋权有向图 之上,如果是无向网,则可以将每条边写成两条单向弧以成为有向网。运筹学是研究达到目标的最优方法的学问,比如从A点到B点最短路径或者最快路径,需要先判断是要最短路径,还是要最快路径。决定了希望的结果后,才能根据此目标去研究方法。
最短路问题(shortest-path-problem)是图论中的经典问题之一,可用来解决管路铺设、线路安装、厂区布局和设备更新等实际问题。基本内容是:假设网络中的每条边都有一个 权重(常用长度、成本、时间等表示),最短路问题的目标是找出 给定两点(通常是源节点和汇节点)之间总权重之和最小的路径。
运筹学(Operations Research)中的一个经典和重要的分支,所研究的问题涉及经济管理、工业工程、交通运输、计算机科学与信息技术、通讯与网络技术等诸多领域。下面将要讨论的最短路问题、最大流问题、最小费用流问题和匹配问题等都是图与网络的基本问题。
运筹学笔记 图与网络分析
图的基本概念与基本定理
一 . 图的基本概念
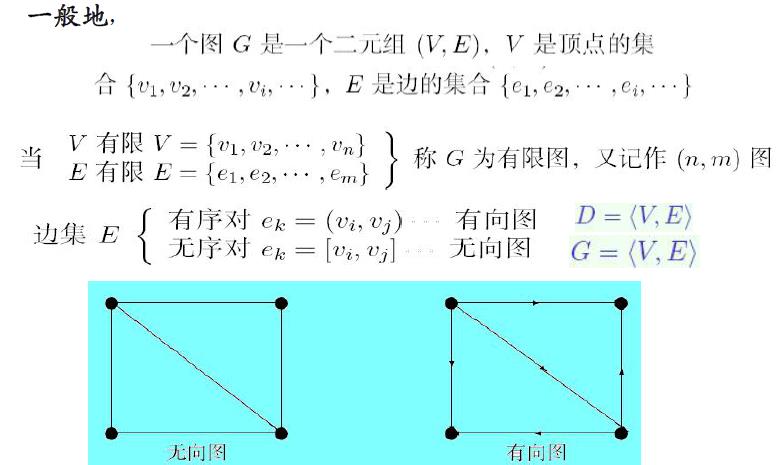
1 . 无向图与有向图

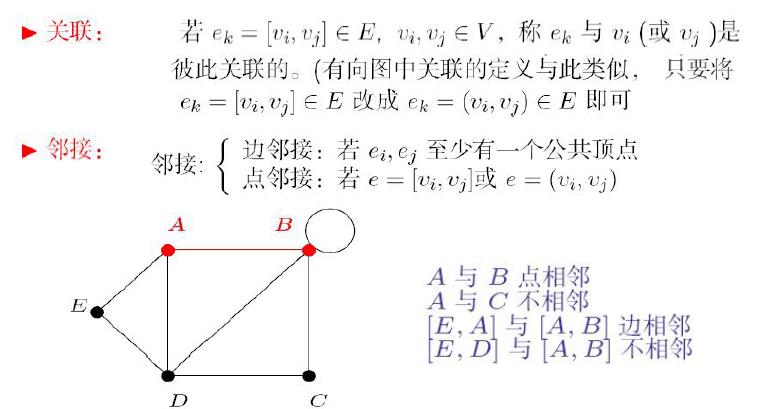
2 . 关联与邻接
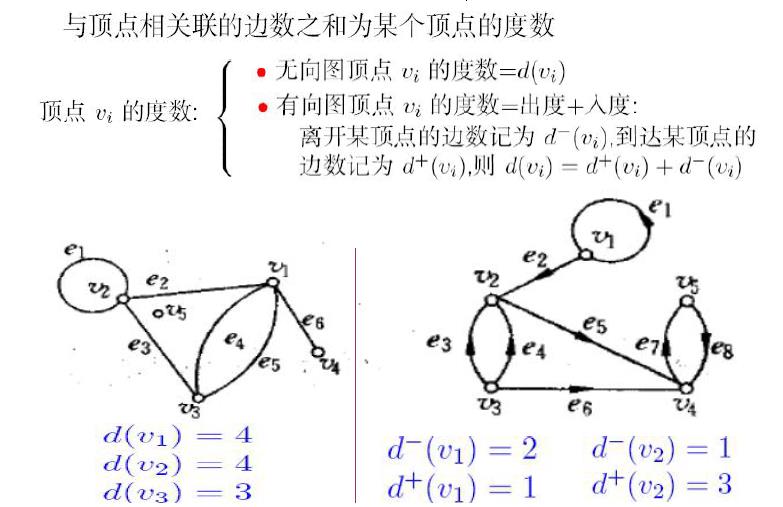
 3. 顶点的度数,图的最大度及最小度
3. 顶点的度数,图的最大度及最小度

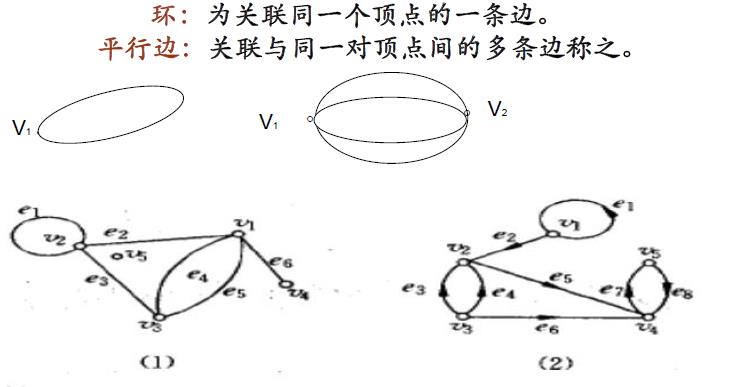
4. 简单图

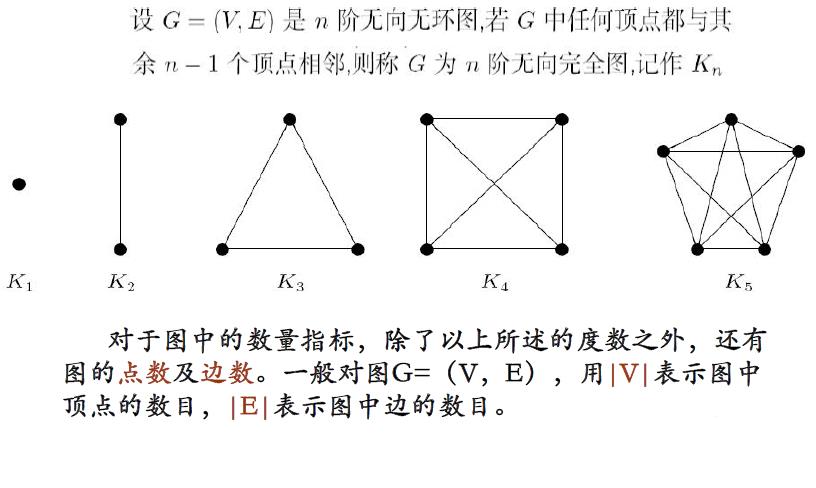
5 . 完全图
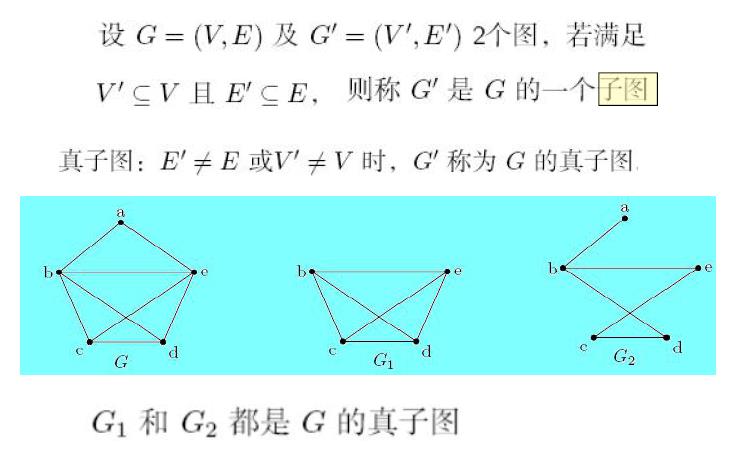
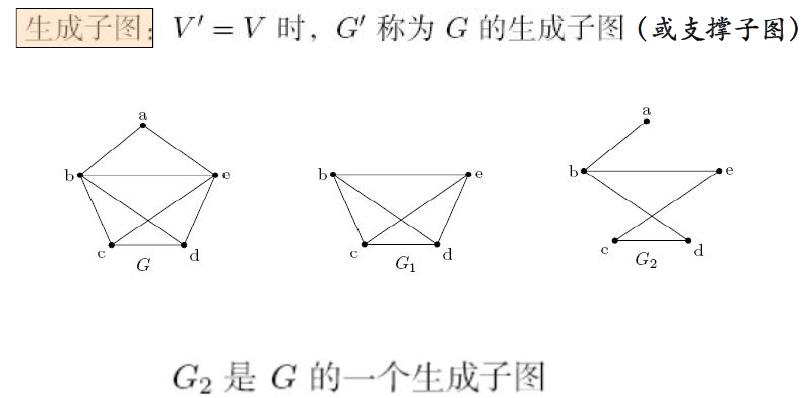
6. 子图、生成子图、补图
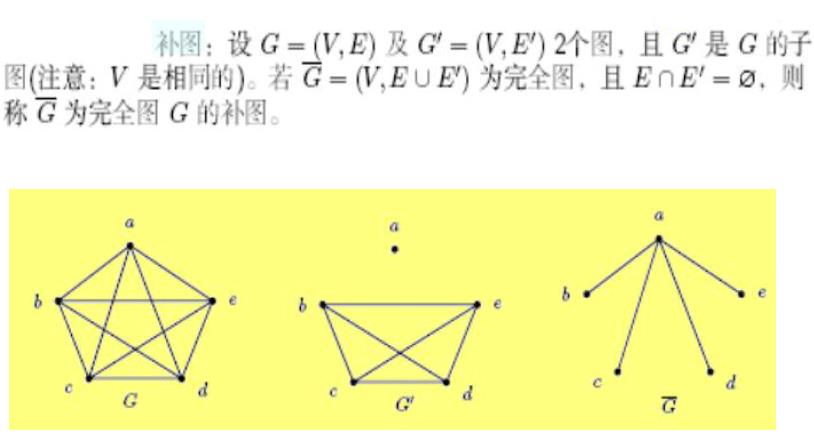
7 . 同构图

8 . 图的通路(或链)、回路(或圈)


9 . 连通图
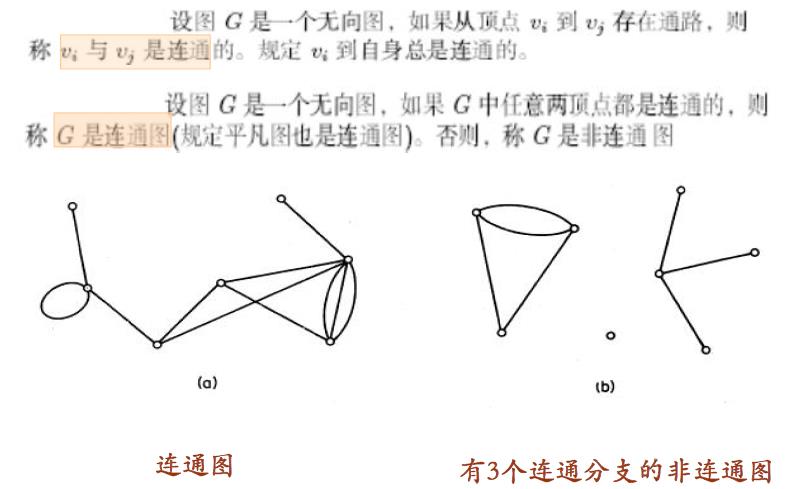
二 . 图的基本定理
定理1:( 握手定理)度数与边数的关系
 推论1: 任意图中度数为奇数的顶点个数必为偶数。
推论1: 任意图中度数为奇数的顶点个数必为偶数。


树和最小生成树
一 . 树及其性质
1 . 定义: 连通而不含回路(圈)的无向图称为无向树,简称树。
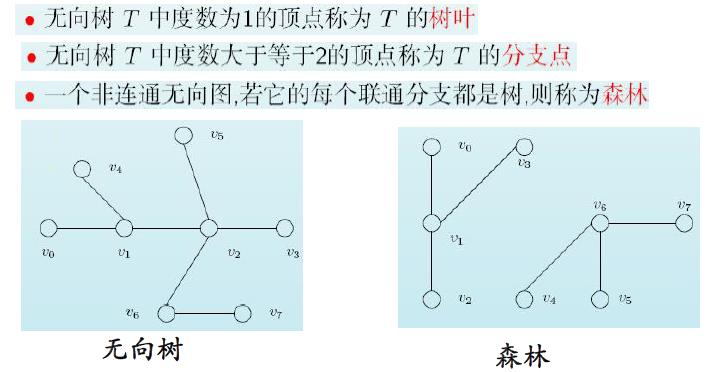 树是连通图中边数最少的图,少一条边,就会不连通,而加一条边就出回路,树正处于临界的状态;
树是连通图中边数最少的图,少一条边,就会不连通,而加一条边就出回路,树正处于临界的状态;
树是图论中最重要的概念之一,又是图论中结构最简单,用途最广泛的一种连通图。例如,同一祖先繁衍的后代按父系血缘关系画出的家谱图就是一棵家族树。
二 . 生成树
1 . 生成树的概念
如果图G的生成子图是一棵树,则该树T称为图G的生成树
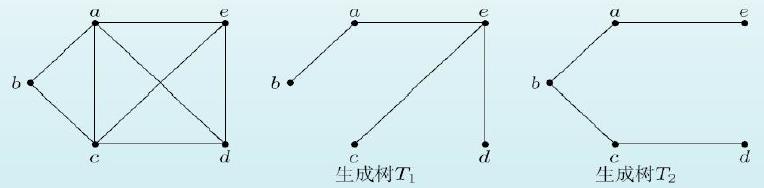
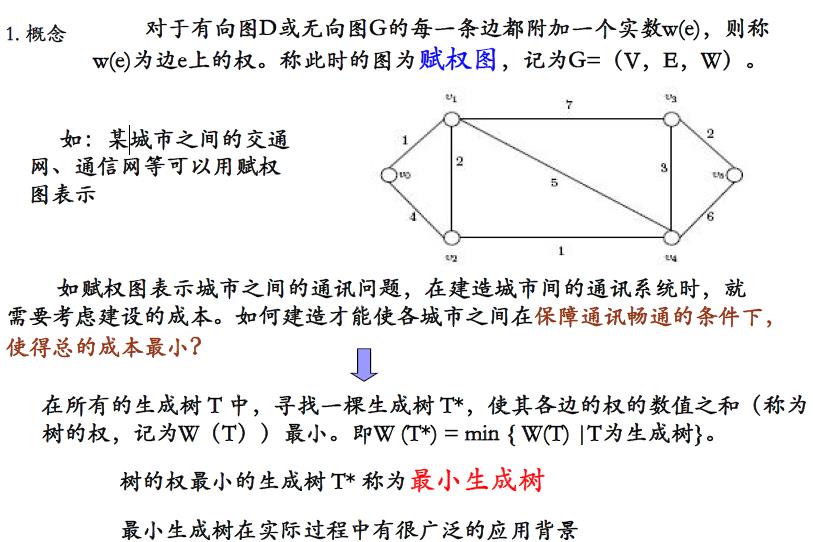
在有线通讯网和交通网中,在保证节点连通的条件下,边数最少(可以节省材料和投资)的线路图必然是生成树,如下图所示 :
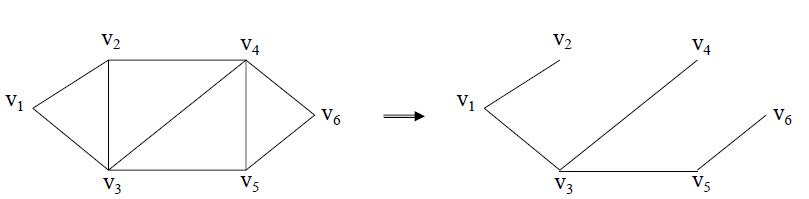
2. 生成树的求法
 上述推导不仅证明了定理的结论,同时给出了生成树的一种构造方法。根据这种方法的特点,我们称其为破圈法。
上述推导不仅证明了定理的结论,同时给出了生成树的一种构造方法。根据这种方法的特点,我们称其为破圈法。
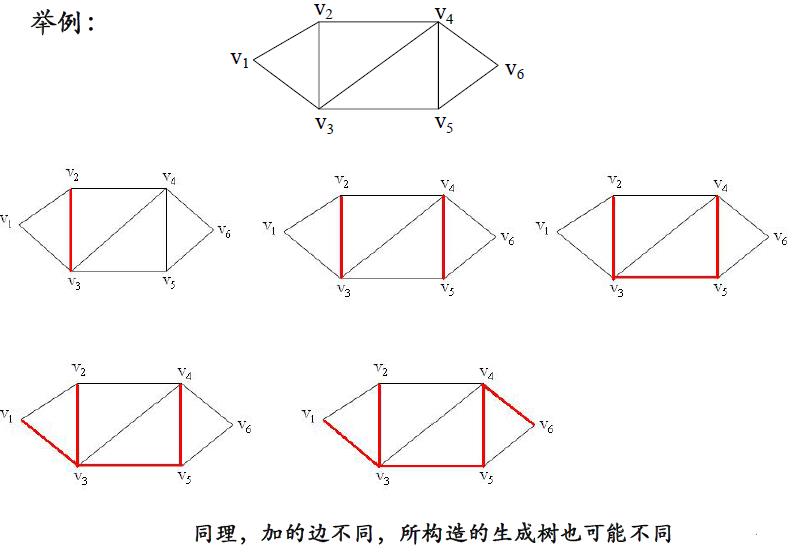
由于破圈过程中,可去掉回路上的任意一条边,因此,去的边不同得到的生成树就可能不同。
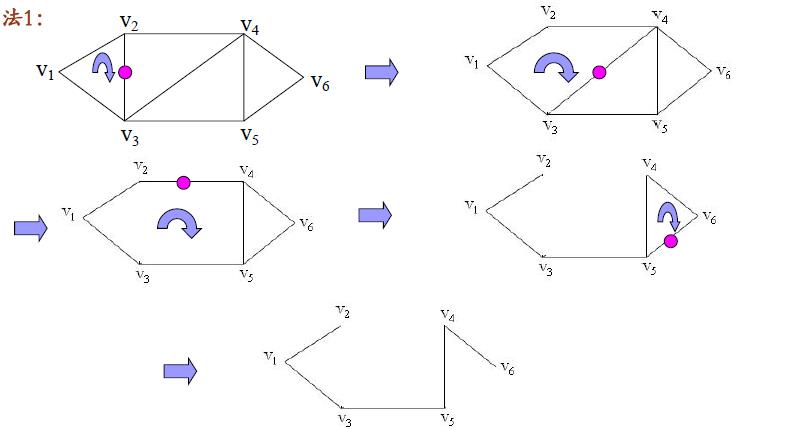
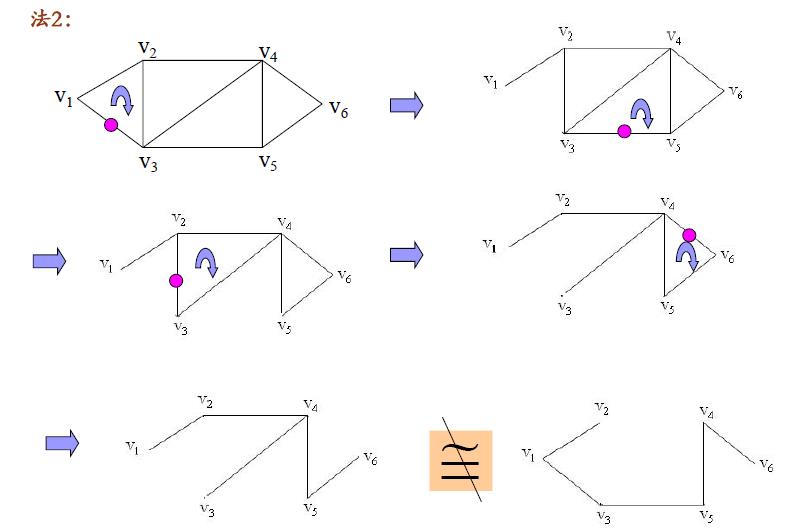
注意破圈法的特点:是先找到一个回路,之后再其上逐渐“去边”。就象对图做剪枝,最后修剪成一棵树。自然我们就会考虑,能否倒过来,用逐渐“加边”的方法得到生成树?这里的关键就在于加边的规则。
每次加的边都成为生成树的边,就必须保证加边时不能出现回路。开始时,可任意选择图G的一条边,之后按无回路的原则加边,直至构造出生成树。将此方法形象的称做避圈法。同理,根据加的边不同,所得到的生成树就可能不同。
生成树的求解方法: 破圈法、避圈法
 3. 图的生成树的变换
3. 图的生成树的变换
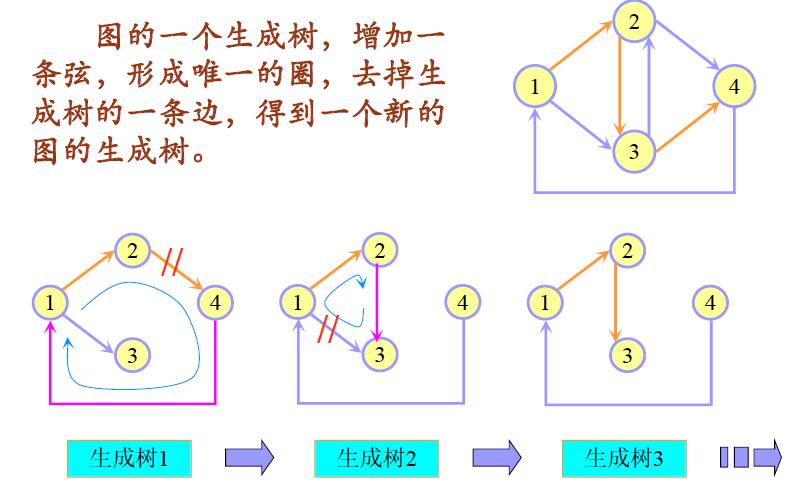
图的一个生成树,增加一条弦,形成唯一的圈,去掉生成树的一条边,得到一个新的图的生成树。
三 . 最小生成树
1.概念
 2. 最小生成树的求法
2. 最小生成树的求法
受前面生成树的构造方法的启发,对于寻找最小生成树,它的关键仍然是在边上做文章,即如何删除或选择边。为了达到所谓的最优,因此在原来没有回路的原则上,必须还要考虑边的权值。这就自然产生了相应的两种求最小生成树的方法,我们同样可以称其为破圈法和避圈法。
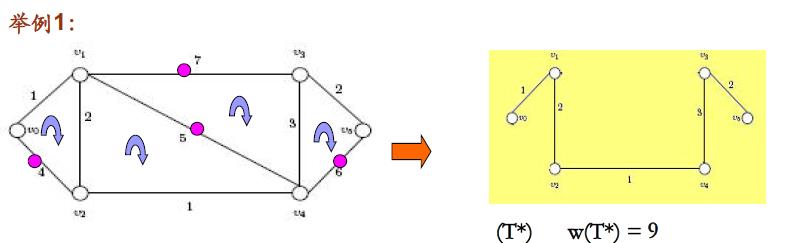
求最小生成树的方法之一: 破圈法
算法的去边原则为:删除回路上最长的边
即整个方法可以简单描述为:任取一个回路后,删除回路上权值最大的边。
 求最小生成树的方法之二:避圈法(又称Kruskal算法)
求最小生成树的方法之二:避圈法(又称Kruskal算法)
方法的思路是:在无回路的原则下,优先地选择权小的边
为了选择权值小的边,在避圈法中需要对图中的边,根据其权值进行排序。

破圈法与避圈法的比较
对某图G,应该采取什么方法寻找最小生成树好,需要具体问题具体分析。
一般来讲,若图中边数较少时用破圈法较好,此时图中的圈少,计算能快一些。但当边数较多时,则用避圈法相对要快一些。另外,从算法的过程来看,破圈法比较简单,容易做。而避圈法,它是通过循环、选择等过程完成,方法上比较系统,特别适合于在计算机上编程实现。
最短路问题
最短路问题是网络理论中应用最广泛的问题之一。如某城市的交通网,因城市内的道路存在单行线。因此描述交通网的图是一个有向图。决定行程时就会遇到,求某地到其它各地的最短路问题。另外许多优化问题可以使用这个模型,如设备更新、管道铺设 、线路安排、厂区布局等。
根据问题的不同,可以将最短路径分为以下两种类型:
• 求图中某一顶点到其它顶点的最短路径。
• 求图中每一对顶点之间的最短路径。
图边中的权W(e) ≥0时的求解方法
确定两点之间距离的较好方法是迪克斯特拉(E.W.Dijkstra)在1959年提出的一个算法, 这一算法至今仍是解这个问题的最好算法

注意:Dijkstra算法只适用于边的权W(e) ≥0情况

Dijkstra算法又称标号法

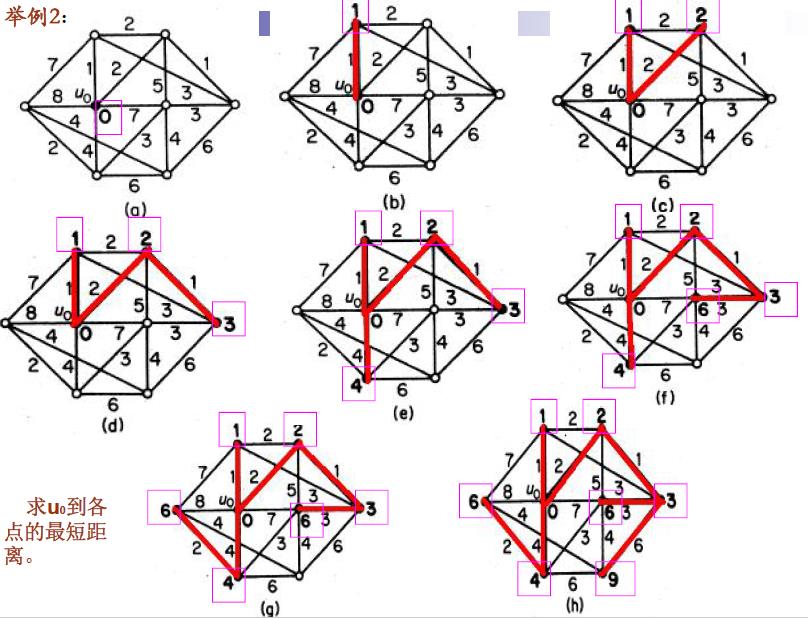
图边中的权W(e) <0时的求解方法
Dijkstra算法仅适合于所有的权wij ≥0的情形。如果当赋权有向图中存在有负权弧时,则该算法失效。
在存在负权时,可采取逐次逼近算法来求解。

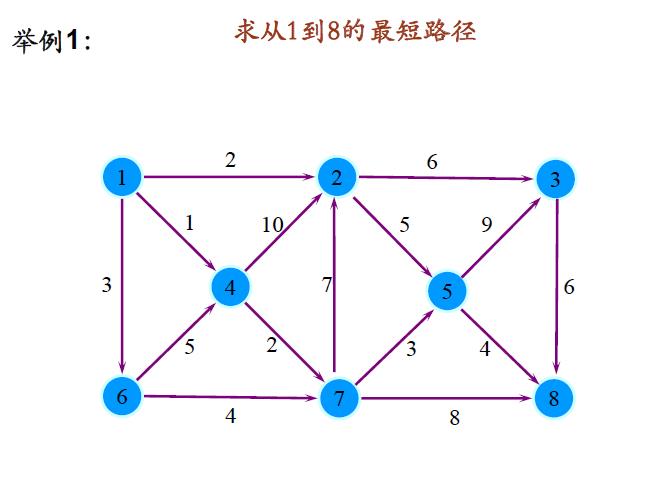
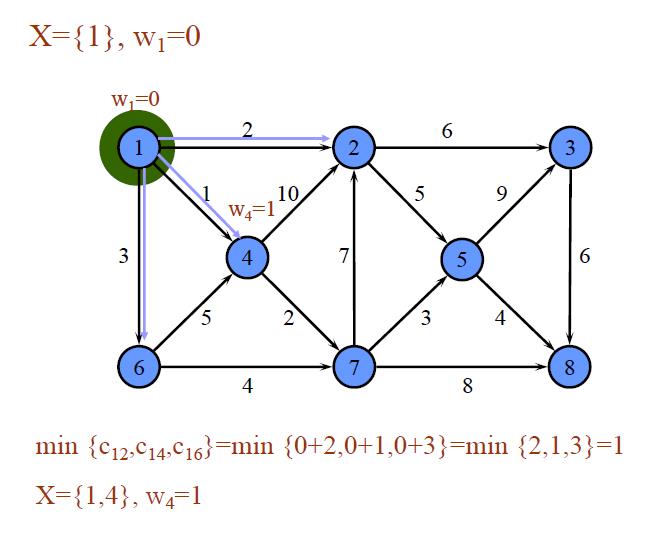
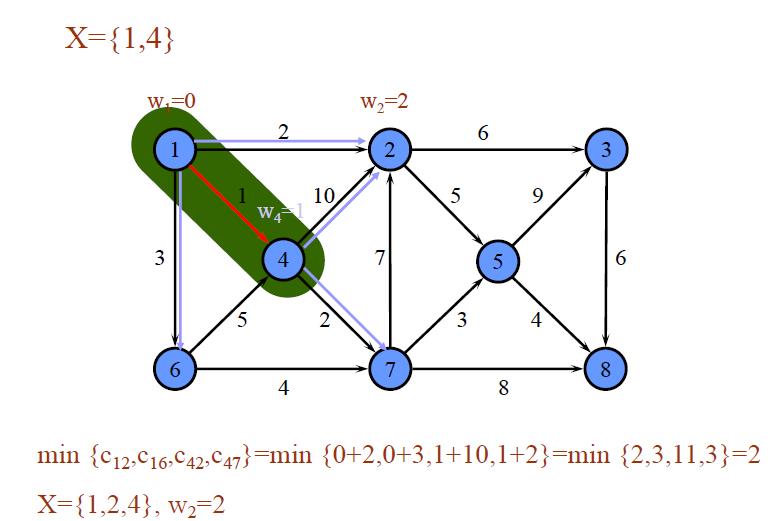
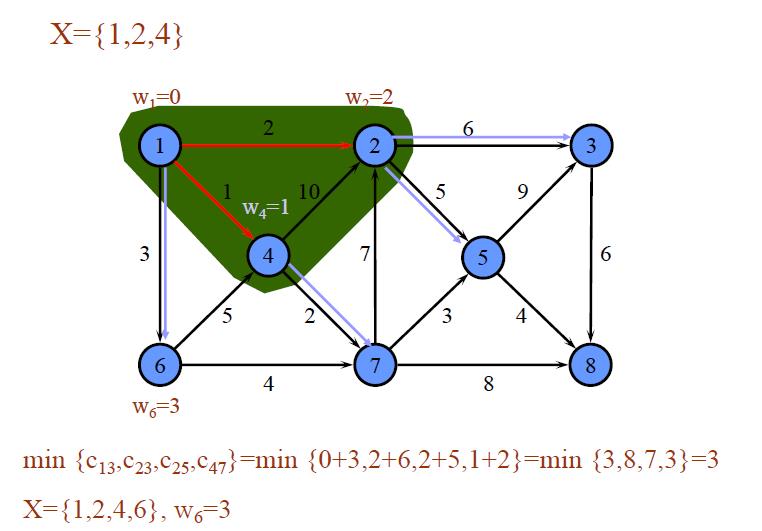
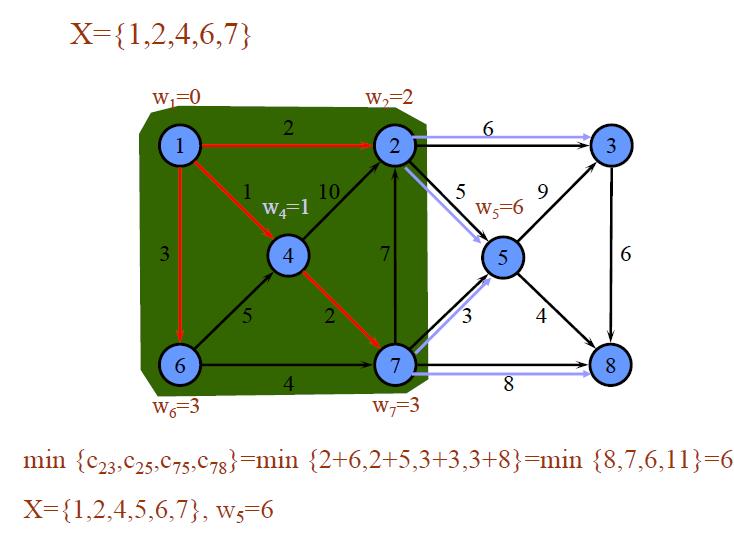
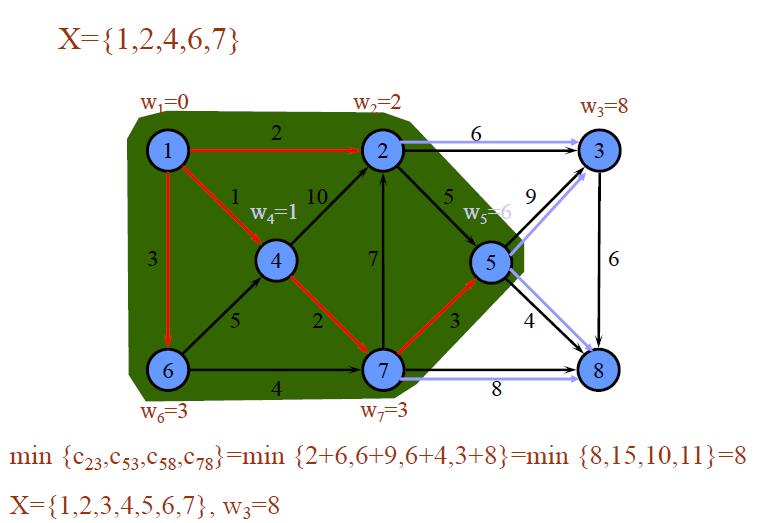
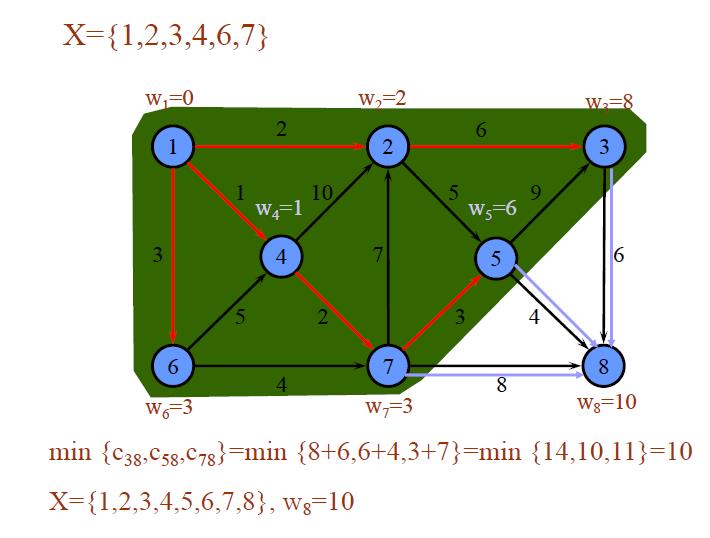
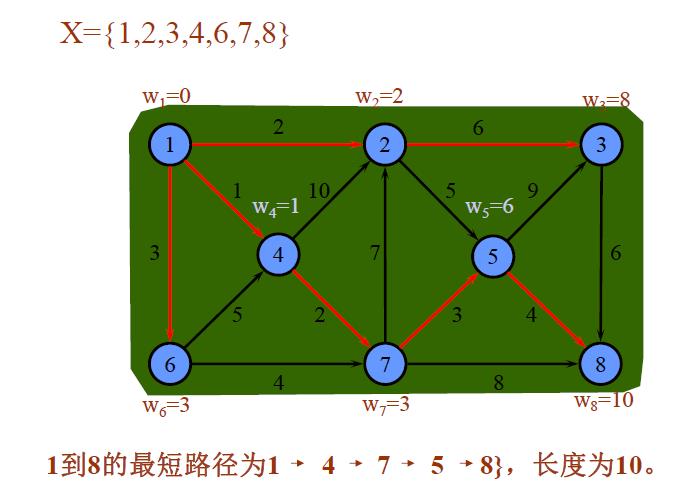
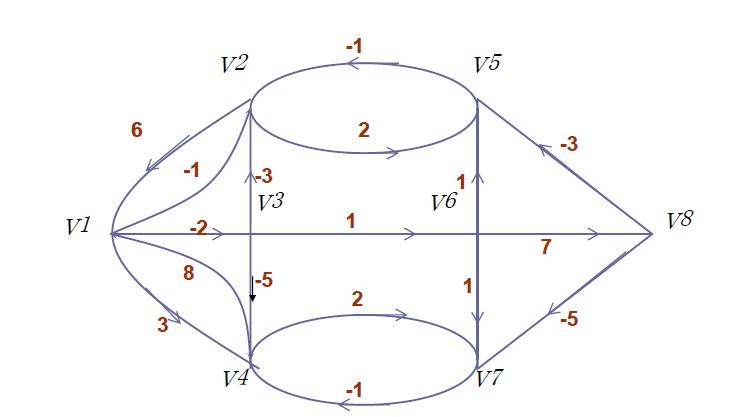
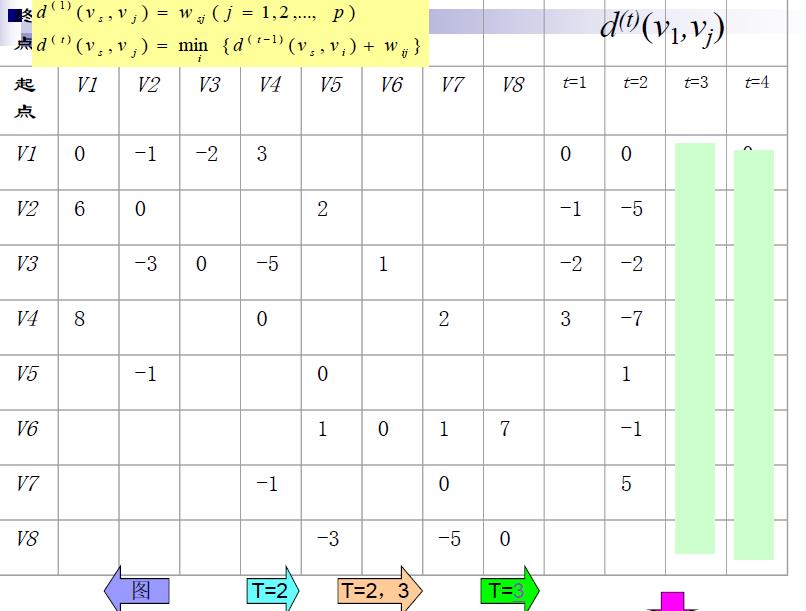
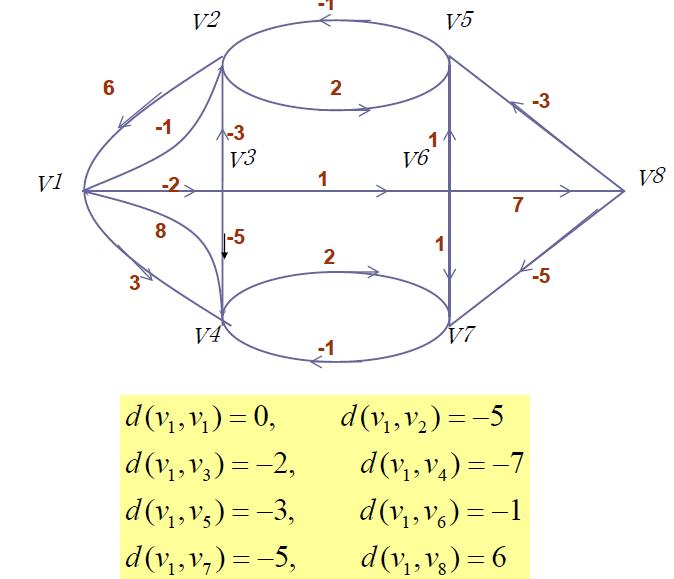
举例1: 对如下赋权有向图,求V1到各点的最短路。


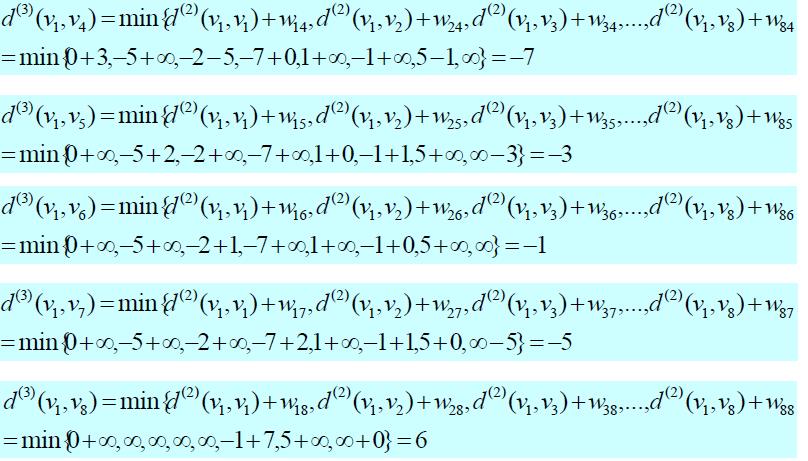

网络系统最大流问题
最大流问题: 给了一个带收发点的网络,其每条有向边的权值称为容量,在不超过每条有向边的容量的前提下,求出从发点到收点的最大流量。
1 . 网络与流
 2. 可行流与最大流
2. 可行流与最大流
对实际的网络系统上的流,有几个特点:
• 发点的总流出量和收点的总流出量必然相等。
• 每一个中间点的流入量与流出量的代数和等于0。
• 每一个有向边上的流量不能超过它的最大通过能力(即流量)。
 显然任意一个网络上的可行流总是存在的。如:v(f)=0
显然任意一个网络上的可行流总是存在的。如:v(f)=0
所谓网络系统的最大流问题,就是求在给定的网络上寻求一个可行流f,使其流量v(f)达到最大,并且满足上面的平衡条件及容量限制。
最大流问题是一个特殊的线性规划问题,但是利用它与图的紧密关系求解更为直观简便。
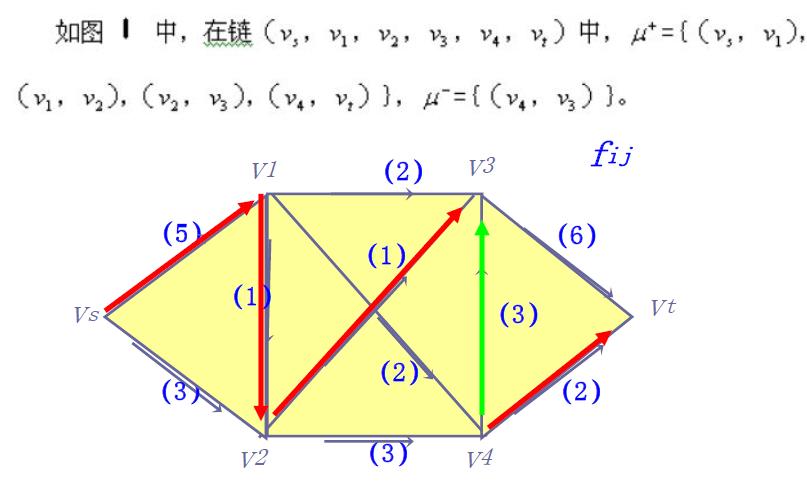
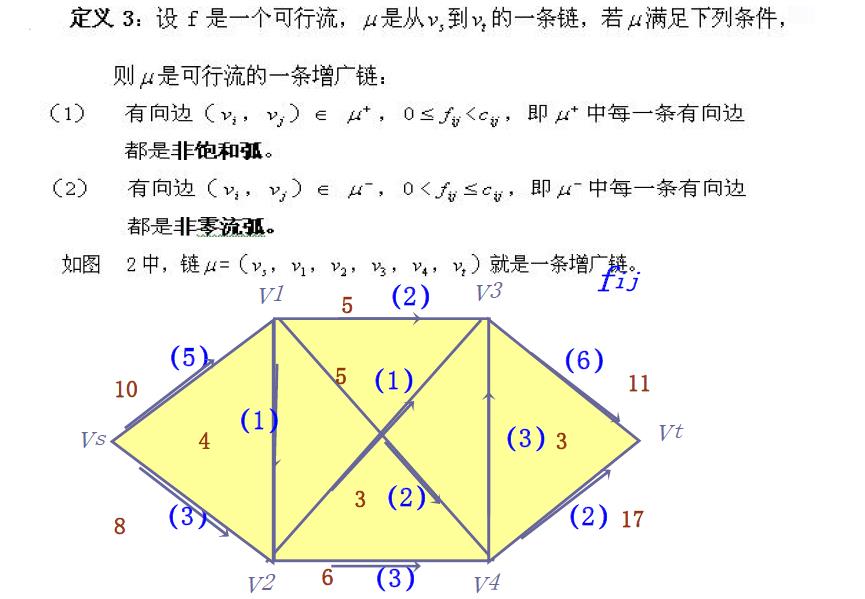
3 . 增广链


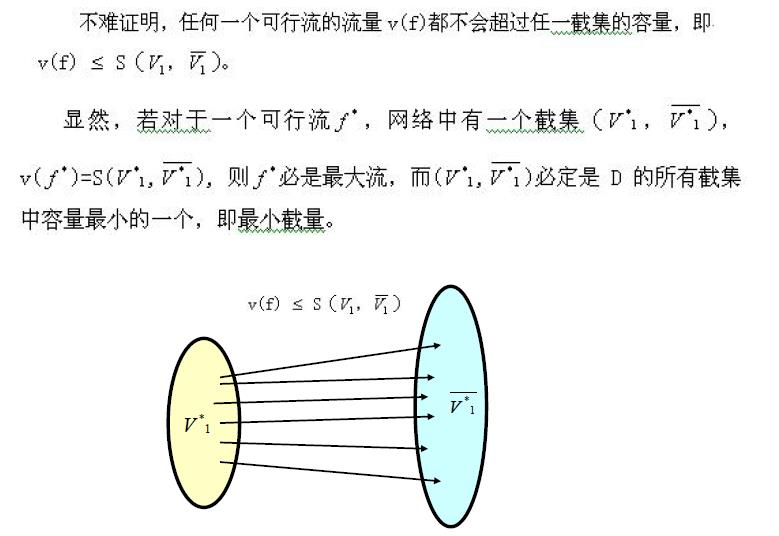 基本定理
基本定理



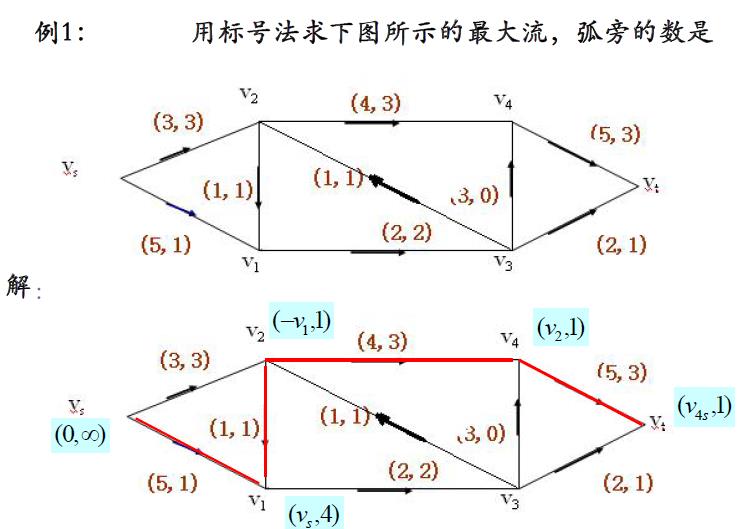
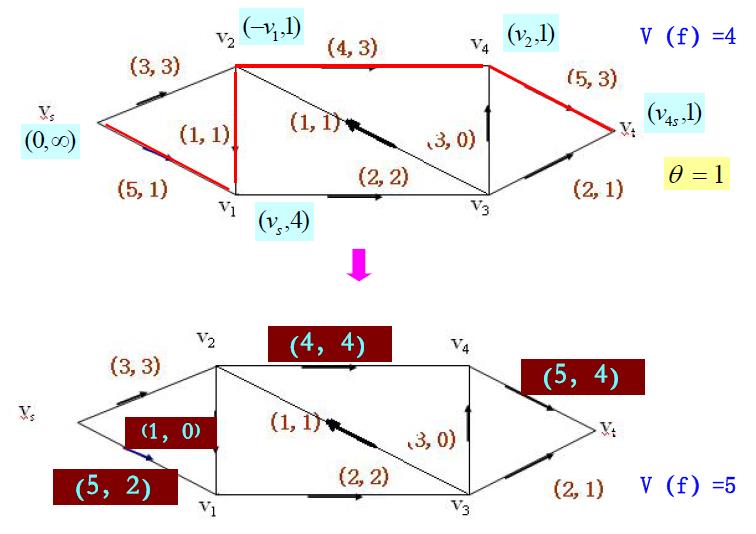
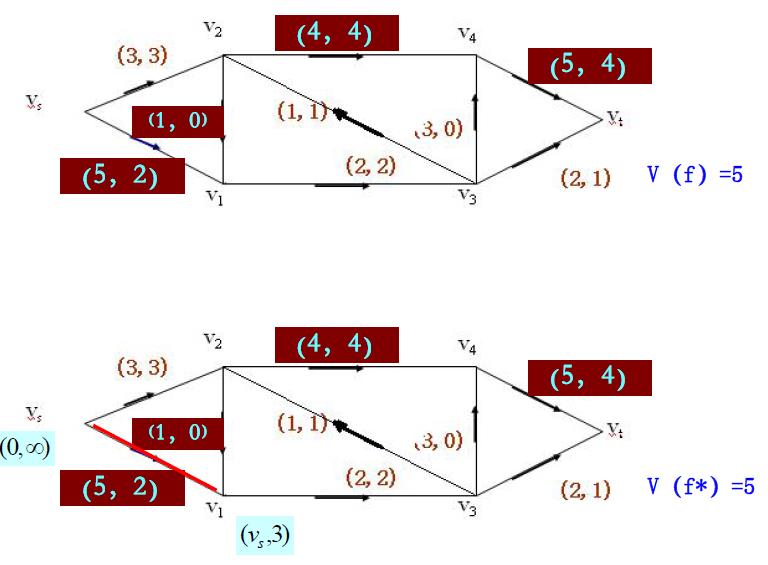
求最大流的标号法
设已有一个可行流(若D中没有f,可以令f为零流),标号算法分2个步骤:
第一步是标号过程,通过标号来寻找增广链;
第二步是调整过程,沿增广链调整 f 以增加流量
- 标号过程



- 调整过程


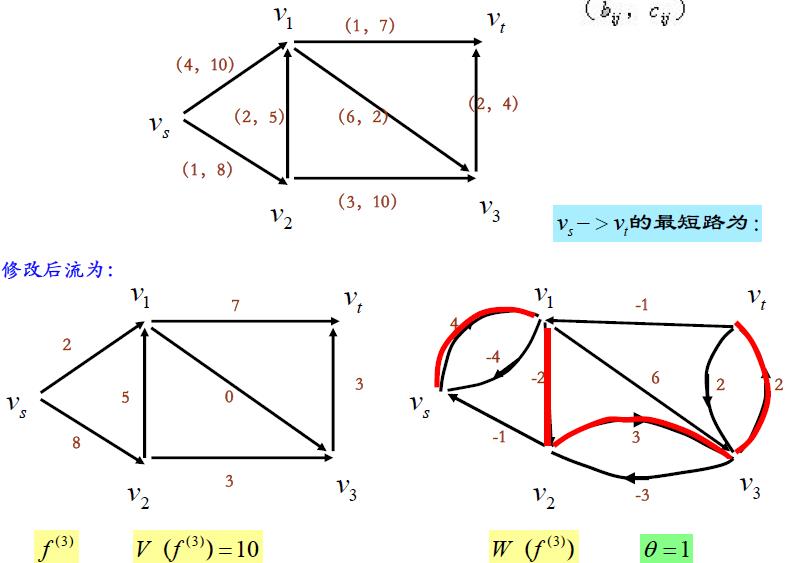
网络系统最小费用最大流问题
在实际的网络系统中,当涉及到有关流的问题时,不仅需要考虑流量,有时还经常要考虑费用的问题。比如一个输油管网络运输系统,既要考虑输油量最大,又要考虑总费用最小。 最小费用最大流问题就是解决此类问题。

一 . 最小费用最大流的数学模型
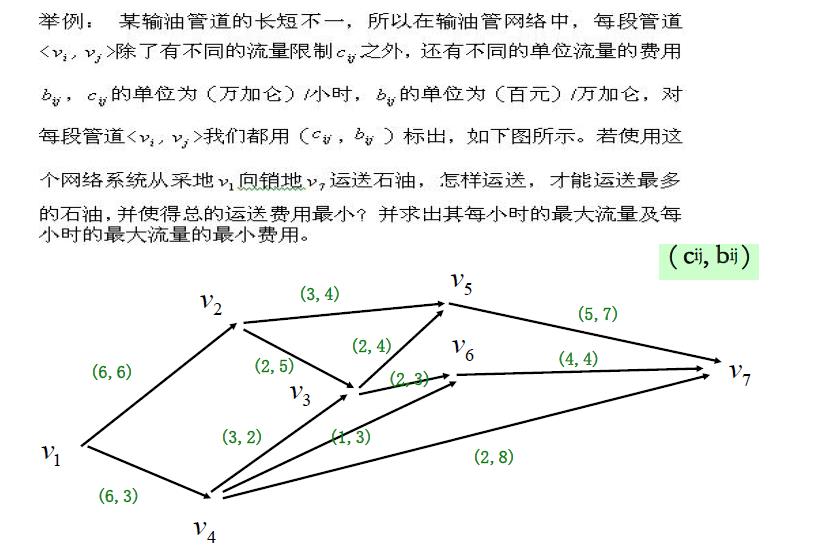
解法1:(线性规划解法)——分2步

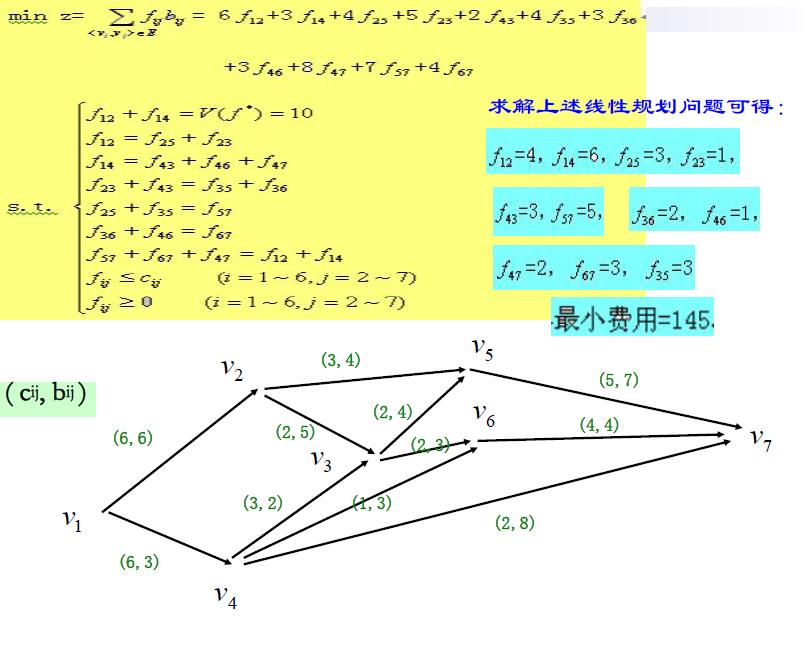
解法2: 网络图论的解法
二 . 最小费用最大流的网络图论解法
最小费用最大流的网络图论的解法类似于求最大流的网络图论方法




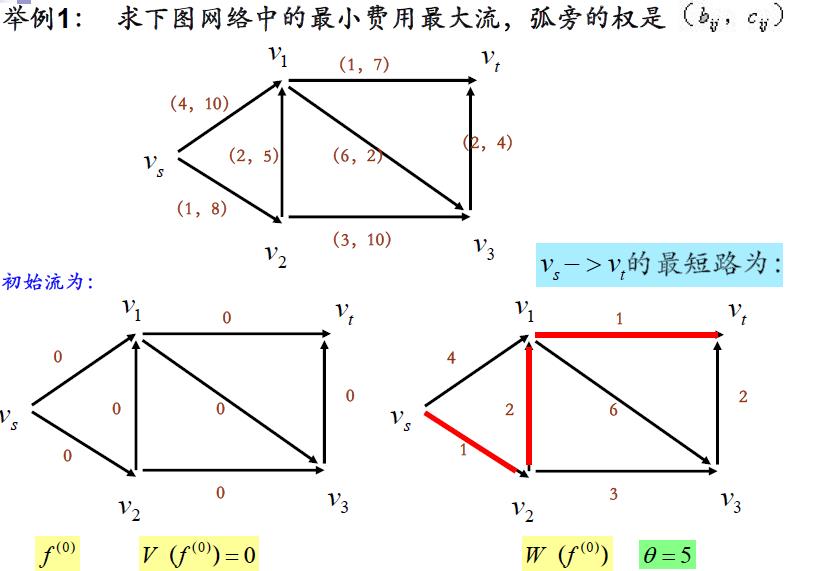
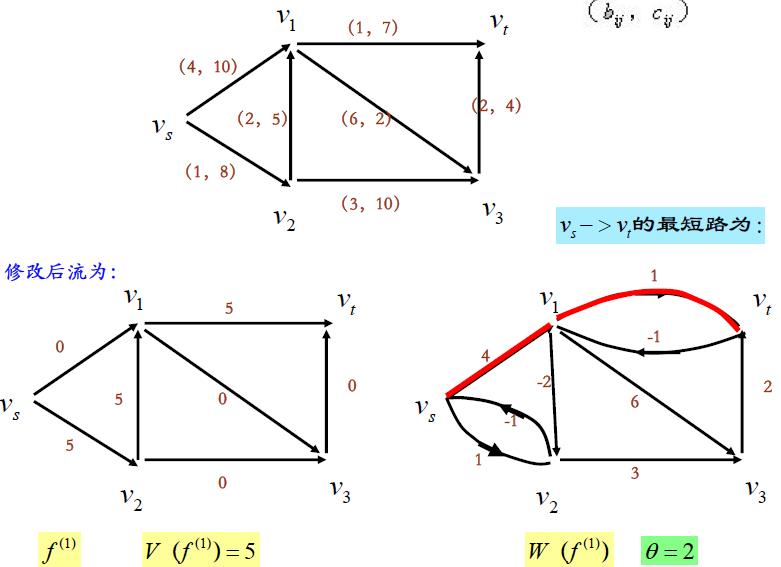
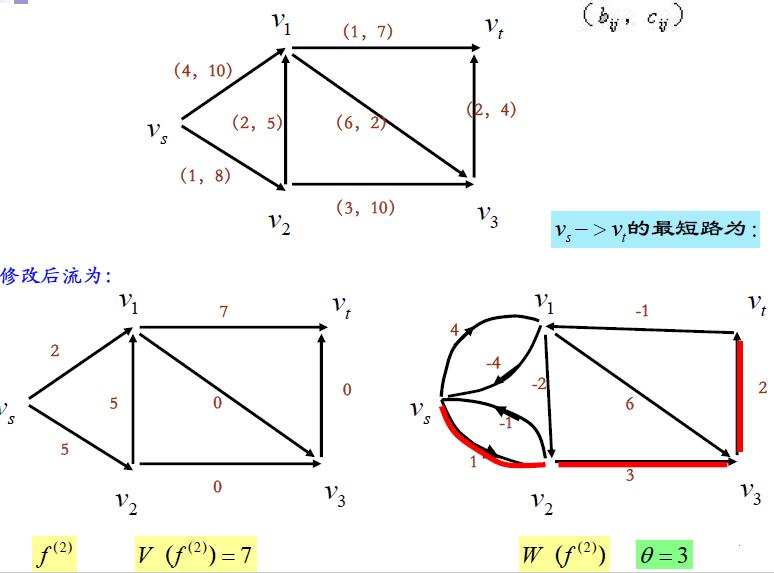
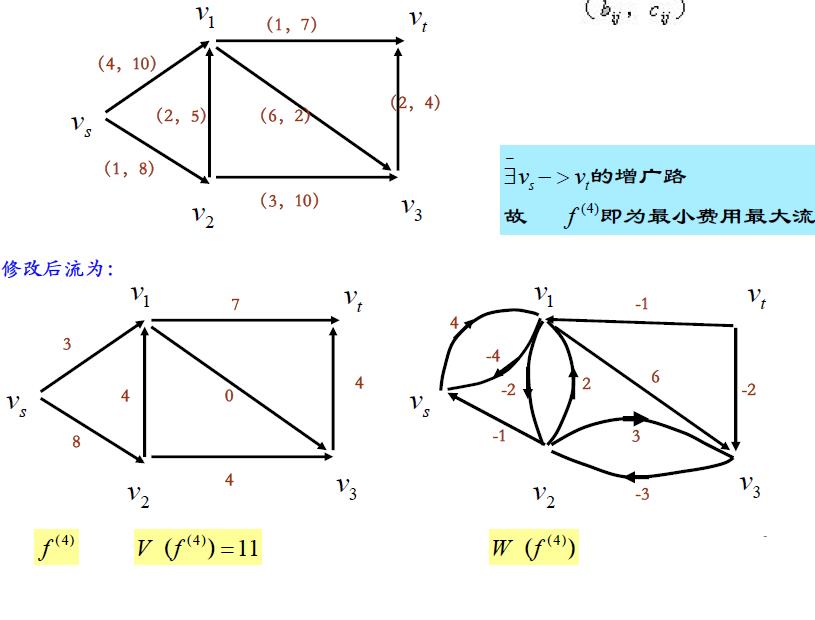
本章介绍了“最小费用最大流问题”、“最大流问题”、和“最短路径问题”三种网络优化问题。
实际,“运输问题”也是一种网络优化问题。
以上四类问题具有许多共同的特征,如都是具有网络结构的线性规划问题。这些问题的变量都是与网络的边对应,约束条件都与网络的节点对应,因此这些问题的线性规划模型中,约束系数矩阵都具有网络问题的特点(不满秩、单位模性质)。

中国邮递员问题
问题:
邮递员从邮局出发,走遍投递区域的所有街道,送完邮件后回到邮局,怎样使所走的路线全程最短.
若街道图(街道的交叉口为顶点)存在欧拉道路,显然此路是全程最短.
一. 欧拉回路问题(一笔画,边的遍历问题)
欧拉链(欧拉道路):经过G的每一条边一次且仅一次的道路称之。
欧拉圈(欧拉回路):经过G的每一条边一次且仅一次的回路称之。
一笔画: 存在欧拉链或欧拉圈的图。
结论1: 一个连通图G是欧拉图的充要条件是G中无度数为奇数的点。
结论2: 一个连通图G有欧拉道路的充要条件是G中有且仅有2个度数为奇数的点。
在许多情况下,图中并不存在欧拉回路。这时如何完成边的遍历问题,使得所走的路径最短。
比如某邮递员从邮局出发,需要遍历他所管辖的每一条街道,将信件送到后返回邮局,要求所走的路径最短。
这个问题是我国的数学家管梅谷先生在1962年首先提出的,因此国际上通常将此类问题称为中国邮路问题。
二. 求解中国邮路问题的图上作业法
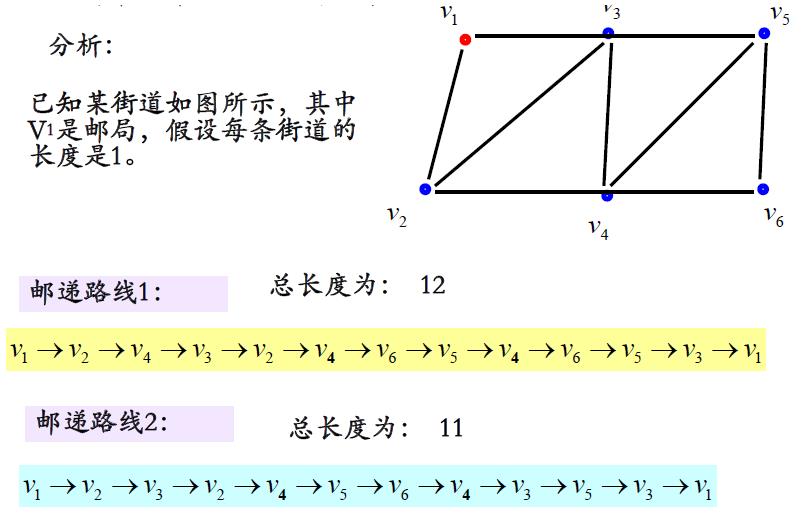
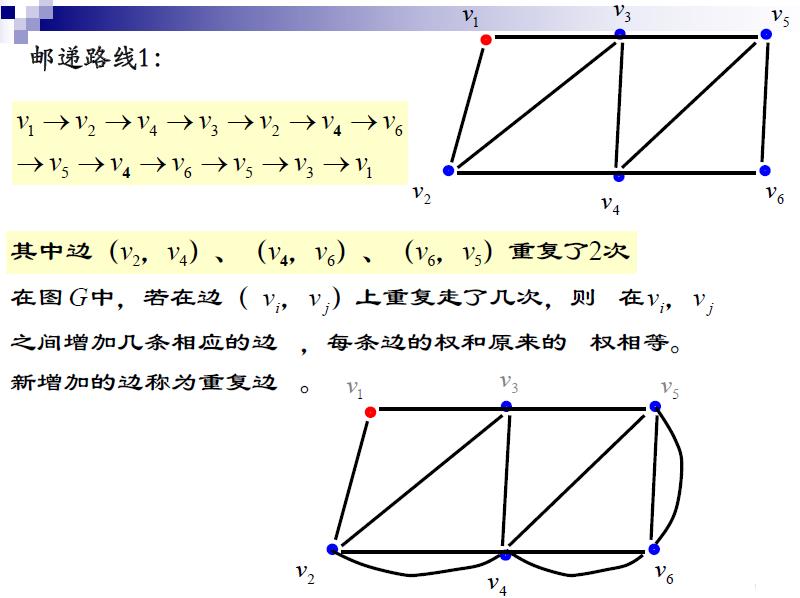
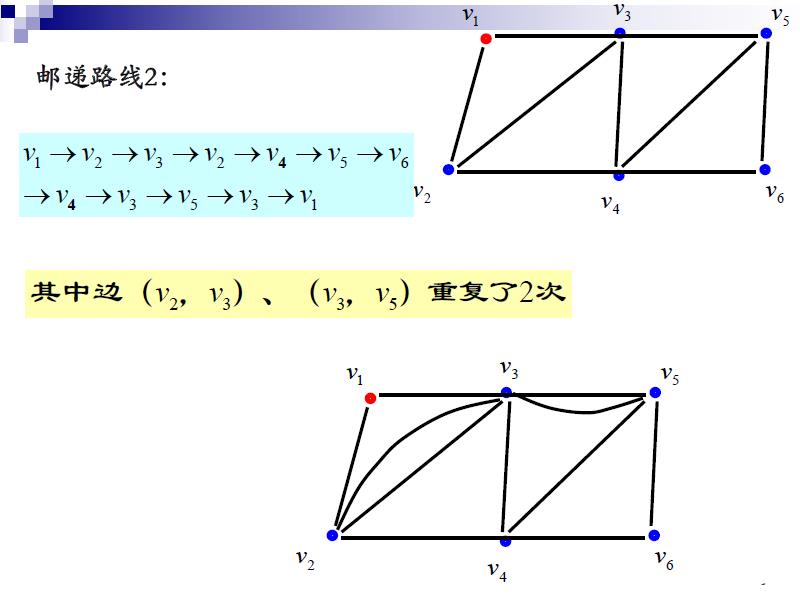
中国邮路问题也可以表示为:
在一个有点的度数为奇数的图中,要求增加一些重复边,使得新的连通图不含有度数为奇数的点,并且增加的重复边总权最小。
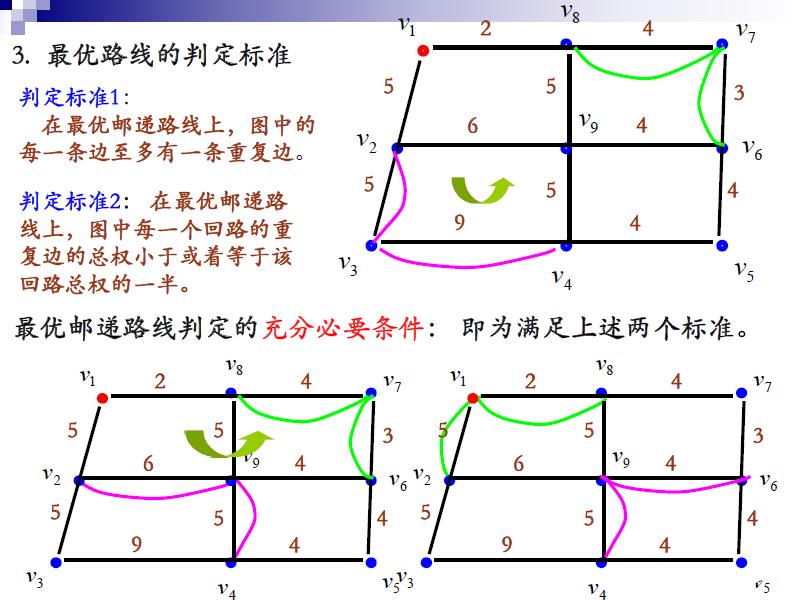
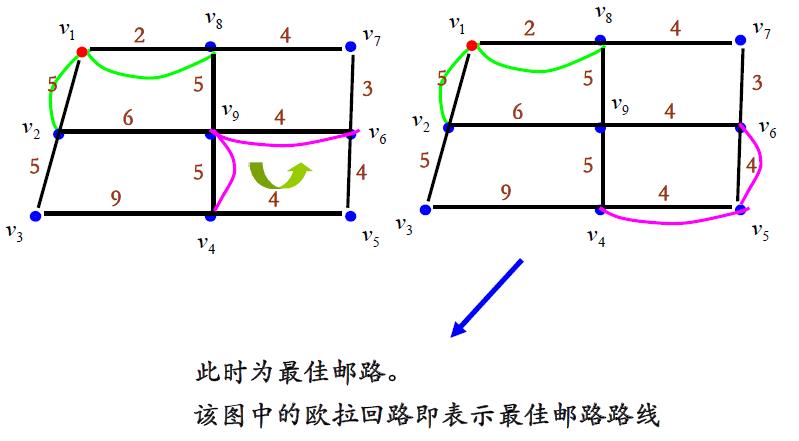
为方便起见,增加重复边后不含奇点的新连通图叫做邮递路线,而总权最小的邮递路线称为最优邮递路线。
下面通过例子分别介绍初始邮递路线的确定、改进,以及一个邮递路线是否是最优路线的判定标准,从而得到求解的图上作业法。
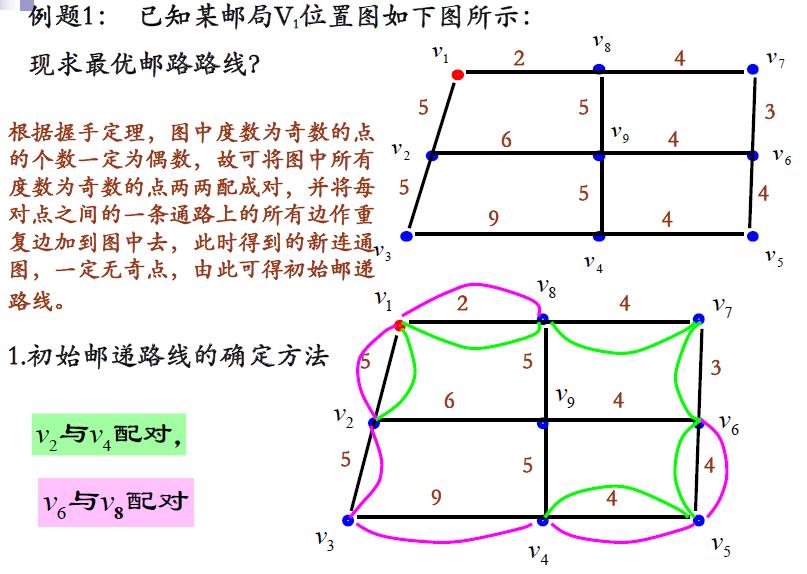
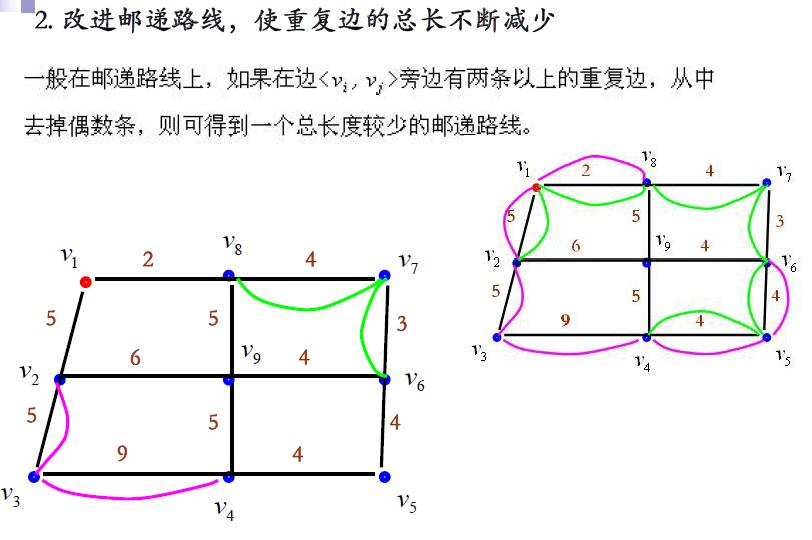
以上是关于运筹学最大流问题?的主要内容,如果未能解决你的问题,请参考以下文章