半对数坐标&matlab实现

Posted 2022-11-25 踏乡墨客

文章目录

• 一、坐标系介绍
• • 1.1 算数坐标系（笛卡尔坐标系）
  • 1.2 对数坐标系
  • 1.3 两者的区别
• 二、基于matlab的实例分析
• • 2.1 举例
  • 2.2 分析与证明

一、坐标系介绍

1.1 算数坐标系（笛卡尔坐标系）

算术坐标系统是普通的笛卡儿坐标，即横纵轴的刻度都是是等距的。

• 举例：如果每1cm的长度都代表1,则刻度按照顺序0,1,2,3,4……，那么在普通的坐标系中，若y=x，则y=x对应的曲线为一条直线。

1.2 对数坐标系

对数坐标系统:坐标轴是按照相等的指数增加变化表示的.举例来说：如果每1cm代表10的1次方增加,则坐标轴刻度的表示依次为1,10,100,1000,10000……

• 对数坐标轴分为半对数和双对数坐标轴。
• 半对数坐标系一个轴是分度均匀的普通坐标轴，另一个轴是分度不均匀的对数坐标轴。
  在对数坐标轴上，某点与原点的实际距离为该点对应数的对数值，但是在该点标出的值是真数（比如y轴是对数坐标轴，1000在坐标轴上画出来与原点的实际距离是3，因为log₁₀(1000)==3，但该点标出的值是10³；在对数坐标轴上与原点实际距离为0,1,2的点分别为10⁰,10¹,10²）。
• 双对数坐标:是指两个坐标轴都是对数坐标，假如对应于x、y轴,则两轴等刻度情况下,其值以相应底数成次方增长.(注意:在各自坐标轴上的是真数（在坐标轴上标的是真数）,不是求对数后的值；因为是对坐标轴进行对数变换，不是对数据点变换。）
  比如x1和y1均为1000(真数)，则坐标轴标的是1000,又求对数后均为3，因此x1和y1在坐标轴上的位置与原点的实际距离是3)
  举例来说：如果每1cm代表10的1次方增加,则坐标轴刻度依次为1,10,100,1000,10000……

1.3 两者的区别

算数坐标系统较对数坐标系统,他们区别体现于等刻度值增长方式不同,一个均匀增长,一个对数增长.

二、基于matlab的实例分析

在Matlab中，semilogx、semilogy函数可分别将x、y坐标轴变换为对数坐标轴。（注：是对坐标轴的改变）

2.1 举例

下面以对y轴进行对数坐标轴变换为例（半对数坐标轴）

• 首先画出普通坐标系下y=10^x对应的曲线(plot命令)
• 然后画出半对数坐标轴(y为对数坐标轴)下y=10^x对应的曲线(semilogy命令)

代码：

 x = 0:0.1:10;
 y = 10.^x;
 
 subplot(2,1,1)
 plot(x,y)
 grid on %打开网格线
 
 subplot(2,1,2)
 semilogy(x, y)

2.2 分析与证明

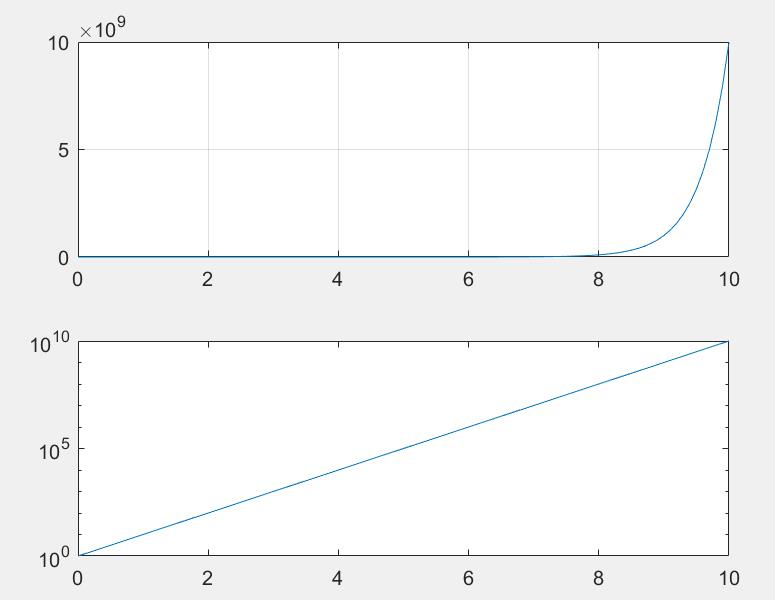
• 第一个图为普通坐标系下y=10^x对应的曲线，是一个以指数增长的曲线
• 第二个图是y轴变换为对数坐标轴后得到的新曲线。仔细观察该图的y轴发现10，100(10²)，1000，10000之间的距离是一样的，但是在一般的笛卡尔坐标系中这是不可能。在对数坐标系中，y轴变成了log₁₀y（即新的坐标轴y’），那么相当于把10，100，1000，10000转化成了1，2，3，4，这样就可以理解了。
• 证明：对y=10^x的两边取对数得lgy=lg(10^x)，即y‘ = lgy = x。这里的y’为变换得到的对数坐标轴，y为原来坐标轴上的数。可以发现，因为y’ = x，所以在对数坐标轴下的曲线为一条直线；但是y’轴上的数还是原来的数（真数，即10⁰,10¹，10²，10³…），不是对数值。
• 整个过程可以理解为：将y轴变换为对数坐标轴y’，原来y轴上的数据点(10⁰，10¹，10²，10³…)没变，其实是坐标轴上的刻度变了，数据点(10⁰，10¹，10²，10³…)在对数坐标轴y’上的刻度为0，1，2，3…，所以在半对数坐标系下y’与x对应的曲线为直线。