Theano中文翻译教程. 基础骗之 More Examples

Posted 2022-11-25 walegahaha

更多的例子

从现在开始系统地学习Theano的基本操作是很有必要的，对于一些基本的Tensor的操作请戳 这里

逻辑函数（Logistic Function）

这里有一个比较直观的例子，相对于前面的一章节所介绍的（两个数的相加）有一些复杂。首先让我们看一下逻辑函数的样子

该函数的表达式为
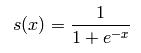
现在你给出一个矩阵，想要对该矩阵里的所有元素都执行这个函数操作，那么你可以采取如下的方法：

>>> import theano
>>> import theano.tensor as T
>>> x = T.dmatrix('x')
>>> s = 1 / (1 + T.exp(-x))
>>> logistic = theano.function([x], s)
>>> logistic([[0, 1], [-1, -2]])
array([[ 0.5       ,  0.73105858],
       [ 0.26894142,  0.11920292]])

为什么这样可以实现对每个元素都进行操作呢？因为所有的这些操作——加法，减法，乘法，初法，求指数——本身都是可以对矩阵中的每一个元素进行操作
由于逻辑函数还可以用另一种方法表示如下，我们可以证实这两种方法所的结果一样。

>>> s2 = (1 + T.tanh(x / 2)) / 2
>>> logistic2 = theano.function([x], s2)
>>> logistic2([[0, 1], [-1, -2]])
array([[ 0.5       ,  0.73105858],
       [ 0.26894142,  0.11920292]])

同时进行多种输出

Theano非常的强大，支持同时输出不同的运算方法。例如，我们可以对两个矩阵a和b同时计算他们的差值，差值的绝对值和平方差。

>>> a, b = T.dmatrices('a', 'b')
>>> diff = a - b
>>> abs_diff = abs(diff)
>>> diff_squared = diff**2
>>> f = theano.function([a, b], [diff, abs_diff, diff_squared])

当我们运行function f 时，它可以返回三个输出

>>> f([[1, 1], [1, 1]], [[0, 1], [2, 3]])
[array([[ 1.,  0.],
       [-1., -2.]]), array([[ 1.,  0.],
       [ 1.,  2.]]), array([[ 1.,  0.],
       [ 1.,  4.]])]

注： 在这里定义输入变量时我们用的是 T.dmatrices()，它可以同时定义多个矩阵变量，而前文 T.dmatrix()一次只能定义一个矩阵变量。

对函数的输入参数设置默认值

假设我们想要定义一个这样的函数，可以算出两个数的和，但是如果你只给第一个变量赋值，第二个变量默认值为1，这也是可以的，你可以采取如下操作

>>> from theano import In
>>> from theano import function
>>> x, y = T.dscalars('x', 'y')
>>> z = x + y
>>> f = function([x, In(y, value=1)], z)
>>> f(33)
array(34.0)
>>> f(33, 2)
array(35.0)

在这里，我们用了 In 这个类，可以设置你定义函数的某个参数的默认值。显而易见，我们定义变量y的默认值为1。即如果你不给y传传入值，则y的值自动取为1;如果你给y传入值，则y的取值为你所传入的。 和python语言一样，如果你想给某个变量设置默认值，则这个变量必须在没有设置默认值的变量的后面，同样，你可以给多个变量设置默认值

>>> x, y, w = T.dscalars('x', 'y', 'w')
>>> z = (x + y) * w
>>> f = function([x, In(y, value=1), In(w, value=2, name='w_by_name')], z)
>>> f(33)
array(68.0)
>>> f(33, 2)
array(70.0)
>>> f(33, 0, 1)
array(33.0)
>>> f(33, w_by_name=1)
array(34.0)
>>> f(33, w_by_name=1, y=0)
array(33.0)

注：经测试 f(33, w=1, y=0)， f(33, w_by_name=1, 0), f(33, y=1, 1)均是错误的 这里我一知半解，意思大概就是 第一个错误：我们用'w_by_name'覆盖了'w'，函数不识别w。 第二和三个错误：因为我们定义了两个关键词y和w_by_name，当你的输入变量有关键词时，它的后面必须也是关键词，因此f(33, y=1, w_by_name=1)和f(33, w_by_name=1, y=0)是正确的 详情请看Theano库中的 Function

共享变量

给函数一个内部变量是也可行的，让我们来做一个累加器：在开始时，累加器的状态（值）设为0，每次循环累加器的值都会因为给定的输入变量而增加。 首先，我们先定义一个累加器。它加上输入变量并传给内部状态，然后返回旧的内部状态。

>>> from theano import shared
>>> state = shared(0)
>>> inc = T.iscalar('inc')
>>> accumulator = function([inc], state, updates=[(state, state+inc)])

这段代码包含了几个新的概念。shared函数构建了一个所谓的共享变量，而这个变量的值可以在多个函数中共享。如同 dmatrices() 的功能一样，只不过这个共享变量包含了一一个可以被很多函数共享的内部值。通过shared() 所定义的变量可以被修改 .get_value()和打印 .set_value。 这段代码中另一个新的概念就是 function 函数中的 updates 参数， 这个参数必须被赋予 （共享变量， 新的表达式）这样的形式。意思就是，每当这个函数运行，共享变量的值值都会通过定义的新的表达式而进行更新。因此我们的累加器才能够成功运行。来让我们试一下吧！

>>> print(state.get_value())
0
>>> accumulator(1)
array(0)
>>> print(state.get_value())
1
>>> accumulator(300)
array(1)
>>> print(state.get_value())
301

当然，共享变量的值可以被重新定义，利用  .set_value() >>> state.set_value(-1)

>>> accumulator(3)
array(-1)
>>> print(state.get_value())
2

正如我们在前面所提到的，你可以定义不止一个函数来共享同一个共享变量，这些函数都可以更新它的值

>>> decrementor = function([inc], state, updates=[(state, state-inc)])
>>> decrementor(2)
array(2)
>>> print(state.get_value())
0

你可能会想这样的共享机制有什么用，你可以用一个新的表达式返回上述同样的结果。这种机制可以使你的代码简洁，不过更主要的是可以提高效率。共享变量在适当的算法上上（例如低阶矩阵的更新）可以运算的非常快。除此之外，Theano可以更好地控制共享变量的分配，是提高GPU性能的一个很重要的方面。 有些时候当你用共享变量计算完某个式子后，却不想要这个值。这种情况下，你可以用 function 中的 givens 参数。

>>> fn_of_state = state * 2 + inc
>>> # The type of foo must match the shared variable we are replacing
>>> # with the ``givens``
>>> foo = T.scalar(dtype=state.dtype)
>>> skip_shared = function([inc, foo], fn_of_state, givens=[(state, foo)])
>>> skip_shared(1, 3)  # we're using 3 for the state, not state.value
array(7)
>>> print(state.get_value())  # old state still there, but we didn't use it
0

这个 givens 参数可以用来替代任何变量，不一定是共享变量，可以是常数也可以是表达式 因此实际操作中，我们可以利用 givens 来用同一类型和长度的不同表达式替换你的表达式的某一项 （笔者一直无法实现这几个操作）

随机数

在Theano中一般是先用各种符号完成表达式，然后再去编译表达式得到函数。在Numpy中用伪随机数虽然简单但是显然是不直观的。 我们一般是先定义随机变量，然后再把随机变量放入 Theano 的计算中来增加随机性。Theano会为每一个随机变量分配一个随机数生成器，什么时候需要什么时候再用。我们称这种随机数列为随机流，而随机流的核心就是共享变量。

简单的例子

这是一个简单的例子，初始代码如下

from theano.tensor.shared_randomstreams import RandomStreams
from theano import function
srng = RandomStreams(seed=234)
rv_u = srng.uniform((2,2))<pre name="code" class="python"><span style="font-family: Arial, Helvetica, sans-serif;">rv_n = srng.normal((2,2))</span>

f = function([], rv_u)g = function([], rv_n, no_default_updates=True) #Not updating rv_n.rngnearly_zeros = function([], rv_u + rv_u - 2 * rv_u)

在这里，'rv_u'代表着一个2 x2的随机流矩阵，里面的数是从均匀分布中取得的。同样'rv_n'也代表着一个2 x2的随机流矩阵，里面的数是从正态分布中取得的。这些分布在 RandomStreams中就被定义好了，在低层次上 raw random。这样的随机数只能用在CPU上，GPU版本请 戳这里 现在我们可以开始使用了， 如果我们调用 f()， 我们得到均匀分布的随机数，内部的随机数生成器可以帮我们自动更新，因此每次调用都会得到不同的随机数

>>> f_val0 = f()
>>> f_val1 = f()  #different numbers from f_val0

当我们给function函数增加一个输入参数 no_default_updates = True时，例如函数g，这样每次调用函数就不会更改随机数的值，两次调用将返回同样的值

>>> g_val0 = g()  # different numbers from f_val0 and f_val1
>>> g_val1 = g()  # same numbers as g_val0!

很重要的一点就是在单独的函数中，每个随机变量最多只会被调用一次，因此在 nearly_zeros函数中，即使该随机变量被调用了3次，还是会得到一个非常接近0的数（除非有时因为舍入误差）。

>>> nearly_zeros = function([], rv_u + rv_u - 2 * rv_u)

种子流

随机变量的种子可以被统一指定（上一节）或者单独指定。通过 .rng.set_value 可以把rv_u分配随机种子的任务交给变量rng_val

>>> rng_val = rv_u.rng.get_value(borrow=True)   # Get the rng for rv_u
>>> rng_val.seed(89234)                         # seeds the generator
>>> rv_u.rng.set_value(rng_val, borrow=True)    # Assign back seeded rng

一般来说，我们定义完随机变量后，先用上一节的方法为所有随机变量的种子设定一个暂时的初值，然后如果有需要，再对个别的随机变量设定其自己的种子值

在函数之间共享种子

如同共享变量一样，随机变量的随机数生成器也可以在不同的函数间共享。因此 nearly_zeros 函数就可以更新 f 函数的随机数生成器的状态

>>> state_after_v0 = rv_u.rng.get_value().get_state()
>>> nearly_zeros()       # this affects rv_u's generator
array([[ 0.,  0.],
       [ 0.,  0.]])
>>> v1 = f()
>>> rng = rv_u.rng.get_value(borrow=True)
>>> rng.set_state(state_after_v0)
>>> rv_u.rng.set_value(rng, borrow=True)
>>> v2 = f()             # v2 != v1
>>> v3 = f()             # v3 == v1

在Theano图之间复制随机状态

有些情况下，用户希望把所有随机数生成器的‘状态’从一个 theano图到另一个 theano图，比如你想要用一个模型的状态去初始化另一个模型的状态。对 theano.tensor.shared_randomstreams.RandomStreams和 theano.sandbox.rng_mrg.MRG_RandomStreams我们可以通过拷贝 state_updates 参数去实现。 每一次从随机流对象得到随机变量，一个元组就会被增加到 state_updates 的列表中。第一个元素是共享变量，代表着随机数生成器的状态;第二个元素代表着theano图，对应着随机数生成过程（例如 RandomFunctionuniform.0）
下面是“随机状态“从一个函数转化到另一个函数的例子。

>>> from __future__ import print_function
>>> import theano
>>> import numpy
>>> import theano.tensor as T
>>> from theano.sandbox.rng_mrg import MRG_RandomStreams
>>> from theano.tensor.shared_randomstreams import RandomStreams

>>> class Graph():
...     def __init__(self, seed=123):
...         self.rng = RandomStreams(seed)
...         self.y = self.rng.uniform(size=(1,))

>>> g1 = Graph(seed=123)
>>> f1 = theano.function([], g1.y)

>>> g2 = Graph(seed=987)
>>> f2 = theano.function([], g2.y)

>>> # By default, the two functions are out of sync.
>>> f1()
array([ 0.72803009])
>>> f2()
array([ 0.55056769])

>>> def copy_random_state(g1, g2):
...     if isinstance(g1.rng, MRG_RandomStreams):
...         g2.rng.rstate = g1.rng.rstate
...     for (su1, su2) in zip(g1.rng.state_updates, g2.rng.state_updates):
...         su2[0].set_value(su1[0].get_value())

>>> # We now copy the state of the theano random number generators.
>>> copy_random_state(g1, g2)
>>> f1()
array([ 0.59044123])
>>> f2()
array([ 0.59044123])

其他随机分布

一个例子：逻辑回归

import numpy
import theano
import theano.tensor as T
rng = numpy.random

N = 400                                   # training sample size
feats = 784                               # number of input variables

# generate a dataset: D = (input_values, target_class)
D = (rng.randn(N, feats), rng.randint(size=N, low=0, high=2))
training_steps = 10000

# Declare Theano symbolic variables
x = T.matrix("x")
y = T.vector("y")

# initialize the weight vector w randomly
#
# this and the following bias variable b
# are shared so they keep their values
# between training iterations (updates)
w = theano.shared(rng.randn(feats), name="w")

# initialize the bias term
b = theano.shared(0., name="b")

print("Initial model:")
print(w.get_value())
print(b.get_value())

# Construct Theano expression graph
p_1 = 1 / (1 + T.exp(-T.dot(x, w) - b))   # Probability that target = 1
prediction = p_1 > 0.5                    # The prediction thresholded
xent = -y * T.log(p_1) - (1-y) * T.log(1-p_1) # Cross-entropy loss function
cost = xent.mean() + 0.01 * (w ** 2).sum()# The cost to minimize
gw, gb = T.grad(cost, [w, b])             # Compute the gradient of the cost
                                          # w.r.t weight vector w and
                                          # bias term b
                                          # (we shall return to this in a
                                          # following section of this tutorial)

# Compile
train = theano.function(
          inputs=[x,y],
          outputs=[prediction, xent],
          updates=((w, w - 0.1 * gw), (b, b - 0.1 * gb)))
predict = theano.function(inputs=[x], outputs=prediction)

# Train
for i in range(training_steps):
    pred, err = train(D[0], D[1])

print("Final model:")
print(w.get_value())
print(b.get_value())
print("target values for D:")
print(D[1])
print("prediction on D:")
print(predict(D[0]))

本文翻译自：http://deeplearning.net/software/theano/tutorial/

并对有些文字进行了适当的删改