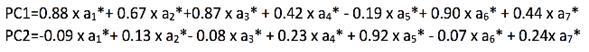PCA原理简介及参考分析实战

Posted 2023-04-12

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了PCA原理简介及参考分析实战相关的知识，希望对你有一定的参考价值。

参考技术A 主成分分析 ( PCA , principal component analysis)是一种数学降维方法, 利用正交变换 (orthogonal transformation)把一系列可能线性相关的变量转换为一组线性不相关的新变量，也称为主成分，从而利用新变量在更小的维度下展示数据的特征。

主成分是原有变量的线性组合，其数目不多于原始变量。组合之后，相当于我们获得了一批新的观测数据，这些数据的含义不同于原有数据，但包含了之前数据的大部分特征，并且有着较低的维度，便于进一步的分析。

在空间上，PCA可以理解为把原始数据投射到一个新的坐标系统，第一主成分为第一坐标轴，它的含义代表了原始数据中多个变量经过某种变换得到的新变量的变化区间；第二成分为第二坐标轴，代表了原始数据中多个变量经过某种变换得到的第二个新变量的变化区间。这样我们把利用原始数据解释样品的差异转变为利用新变量解释样品的差异。

这种投射方式会有很多，为了最大限度保留对原始数据的解释，一般会用最大方差理论或最小损失理论，使得第一主成分有着最大的方差或变异数 (就是说其能尽量多的解释原始数据的差异)；随后的每一个主成分都与前面的主成分正交，且有着仅次于前一主成分的最大方差 (正交简单的理解就是两个主成分空间夹角为90°，两者之间无线性关联，从而完成去冗余操作)。

主成分分析的意义

简化运算。

在问题研究中，为了全面系统地分析问题，我们通常会收集众多的影响因素也就是众多的变量。这样会使得研究更丰富，通常也会带来较多的冗余数据和复杂的计算量。

比如我们我们测序了100种样品的基因表达谱借以通过分子表达水平的差异对这100种样品进行分类。在这个问题中，研究的变量就是不同的基因。每个基因的表达都可以在一定程度上反应样品之间的差异，但某些基因之间却有着调控、协同或拮抗的关系，表现为它们的表达值存在一些相关性，这就造成了统计数据所反映的信息存在一定程度的冗余。另外假如某些基因如持家基因在所有样本中表达都一样，它们对于解释样本的差异也没有意义。这么多的变量在后续统计分析中会增大运算量和计算复杂度，应用PCA就可以在尽量多的保持变量所包含的信息又能维持尽量少的变量数目，帮助简化运算和结果解释。

去除数据噪音。

比如说我们在样品的制备过程中，由于不完全一致的操作，导致样品的状态有细微的改变，从而造成一些持家基因也发生了相应的变化，但变化幅度远小于核心基因 (一般认为噪音的方差小于信息的方差）。而PCA在降维的过程中滤去了这些变化幅度较小的噪音变化，增大了数据的信噪比。

利用散点图实现多维数据可视化。

在上面的表达谱分析中，假如我们有1个基因，可以在线性层面对样本进行分类；如果我们有2个基因，可以在一个平面对样本进行分类；如果我们有3个基因，可以在一个立体空间对样本进行分类；如果有更多的基因，比如说n个，那么每个样品就是n维空间的一个点，则很难在图形上展示样品的分类关系。利用PCA分析，我们可以选取贡献最大的2个或3个主成分作为数据代表用以可视化。这比直接选取三个表达变化最大的基因更能反映样品之间的差异。（利用Pearson相关系数对样品进行聚类在样品数目比较少时是一个解决办法）

发现隐性相关变量。

我们在合并冗余原始变量得到主成分过程中，会发现某些原始变量对同一主成分有着相似的贡献，也就是说这些变量之间存在着某种相关性，为相关变量。同时也可以获得这些变量对主成分的贡献程度。对基因表达数据可以理解为发现了存在协同或拮抗关系的基因。

示例展示原始变量对样品的分类

假设有一套数据集，包含100个样品中某一基因的表达量。如下所示，每一行为一个样品，每一列为基因的表达值。这也是做PCA分析的基本数据组织方式，每一行代表一个样品，每一列代表一组观察数据即一个变量。

Expression profile for Gene1 in 100 samples

PCA分析可参考：

https://www.plob.org/article/11869.html

https://www.jianshu.com/p/f8dc1eb78279

PCA注意事项

一般说来，在PCA之前原始数据需要中心化（centering，数值减去平均值）。中心化的方法很多，除了平均值中心化（mean-centering）外，还包括其它更稳健的方法，比如中位数中心化等。

除了中心化以外，定标 (Scale, 数值除以标准差) 也是数据前处理中需要考虑的一点。如果数据没有定标，则原始数据中方差大的变量对主成分的贡献会很大。数据的方差与其量级成指数关系，比如一组数据(1,2,3,4)的方差是1.67，而(10,20,30,40)的方差就是167,数据变大10倍，方差放大了100倍。

但是定标(scale)可能会有一些负面效果，因为定标后变量之间的权重就是变得相同。如果我们的变量中有噪音的话，我们就在无形中把噪音和信息的权重变得相同，但PCA本身无法区分信号和噪音。在这样的情形下，我们就不必做定标。

一般而言，对于度量单位不同的指标或是取值范围彼此差异非常大的指标不直接由其协方差矩阵出发进行主成分分析，而应该考虑对数据的标准化。比如度量单位不同，有万人、万吨、万元、亿元，而数据间的差异性也非常大，小则几十大则几万，因此在用协方差矩阵求解主成分时存在协方差矩阵中数据的差异性很大。在后面提取主成分时发现，只提取了一个主成分，而此时并不能将所有的变量都解释到，这就没有真正起到降维的作用。此时就需要对数据进行定标(scale)，这样提取的主成分可以覆盖更多的变量，这就实现主成分分析的最终目的。但是对原始数据进行标准化后更倾向于使得各个指标的作用在主成分分析构成中相等。对于数据取值范围不大或是度量单位相同的指标进行标准化处理后，其主成分分析的结果与仍由协方差矩阵出发求得的结果有较大区别。这是因为对数据标准化的过程实际上就是抹杀原有变量离散程度差异的过程，标准化后方差均为1，而实际上方差是对数据信息的重要概括形式，也就是说，对原始数据进行标准化后抹杀了一部分重要信息，因此才使得标准化后各变量在主成分构成中的作用趋于相等。因此，对同度量或是取值范围在同量级的数据还是直接使用非定标数据求解主成分为宜。

中心化和定标都会受数据中离群值（outliers）或者数据不均匀（比如数据被分为若干个小组）的影响，应该用更稳健的中心化和定标方法。

PCA也存在一些限制，例如它可以很好的解除线性相关，但是对于高阶相关性就没有办法了，对于存在高阶相关性的数据，可以考虑Kernel PCA，通过Kernel函数将非线性相关转为线性相关，关于这点就不展开讨论了。另外，PCA假设数据各主特征是分布在正交方向上，如果在非正交方向上存在几个方差较大的方向，PCA的效果就大打折扣了。

主成分分析（PCA）原理及R语言实现

如果你的职业定位是数据分析师/计算生物学家，那么不懂PCA、t-SNE的原理就说不过去了吧。跑通软件没什么了不起的，网上那么多教程，copy一下就会。关键是要懂其数学原理，理解算法的假设，适合解决什么样的问题。

学习可以高效，但却没有捷径，你终将为自己的思维懒惰和行为懒惰买单。

PCA的原理和普通实现

PCA原理

2019年05月16日

用了这么久的PCA，看了很多人的讲解，基本上都是一上来就讲协方差矩阵、特征值、特征向量和奇异值分解，其实这对新手是非常不友好的。

PCA只是一种思想，核心就是线性变化，线性代数里的工具只是一种高效的实现PCA的手段，但并不是唯一的工具。

PCA的核心思想：假设我们的数据有D1, D2,···,Dn个维度，PCA就是要构造一个线性变换，PCi = W1D1 + W2D2 +···+ WnDn，Wj就是第j维度在第i个PC中的权重。找PC有先后顺序，我们总是先找总方差最大的PC，方差解释度是统计里最重要的一个概念。然后我们再找与前一个PC线性无关的能解释最多方差的下一个PC，以此类推，知道得到所有的n个PC。最终的结果就是原先的n个维度通过线性变换，变成了新的n个线性无关的按方差解释度排序的PC。主成分中的“主principal”针对的就是方差解释度。

先从一个玩具的案例开始，熟悉的R数据mtcars，取其中1、3列，二维可视化方便些：

                   mpg disp
Mazda RX4         21.0  160
Mazda RX4 Wag     21.0  160
Datsun 710        22.8  108
Hornet 4 Drive    21.4  258
Hornet Sportabout 18.7  360
Valiant           18.1  225

我们先用R的prcomp包跑一下，熟悉一下PCA的输入输出：

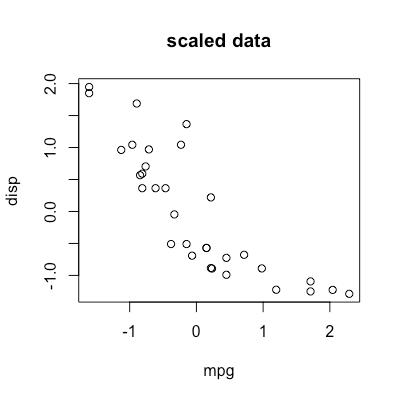
my_data <- mtcars[,c(1,3)]
head(my_data)
plot(my_data, main="raw data")
my_data <- scale(my_data, center = T, scale = T)
plot(my_data, main = "scaled data")
# mtcars.pca <- prcomp(mtcars[,c(1:7,10,11)], center = TRUE,scale. = TRUE)
mtcars.pca <- prcomp(my_data, center = F,scale. = F)
summary(mtcars.pca)
plot(mtcars.pca$x, main = "after PCA")

Importance of components:
                          PC1     PC2
Standard deviation     1.3592 0.39045
Proportion of Variance 0.9238 0.07622
Cumulative Proportion  0.9238 1.00000

PCA的输入很简单，就是一个矩阵，行为样本，列为维度/特征；

这里我把scale这一步单独列出来了，大家可以看下scale的效果是什么，PCA的原始数据如果没有scale，PCA的结果就是错的，因为PCA非常看重方差占比，我们的数据的单位往往千差万别，必须scale，使得不同维度的方差可比。

PCA的输出，sdev、rotation、x；sdev标准差是每个PCA的方差解释度的平方根，肯定是递减的；rotation旋转，很形象，PCA只是把原维度做了旋转而已，rotation是个矩阵里面就是原维度如何通过线性变换，得到PC的；x就是PCA之后原来数据在新的PC下的坐标。

sdev	
the standard deviations of the principal components (i.e., the square roots of the eigenvalues of the covariance/correlation matrix, though the calculation is actually done with the singular values of the data matrix).
rotation	
the matrix of variable loadings (i.e., a matrix whose columns contain the eigenvectors). The function princomp returns this in the element loadings.
x	
if retx is true the value of the rotated data (the centred (and scaled if requested) data multiplied by the rotation matrix) is returned. Hence, cov(x) is the diagonal matrix diag(sdev^2). 
For the formula method, napredict() is applied to handle the treatment of values omitted by the na.action.

输入输出明确了，接下来我们开始做一些个性化的事情：

1. 如果我有新的数据，如何看它在原PCA里的位置？

看下PC是如何得到的，从rotation里我们可以得到线性变换的方程。

            PC1       PC2
mpg  -0.7071068 0.7071068
disp  0.7071068 0.7071068

PC1 = -0.7071068 * mpg + 0.7071068 * disp

PC2 = 0.7071068 * mpg + 0.7071068 * disp

把新数据代入到这个方程里就可以求新数据的PC score了，在R里，一般用矩阵乘法实现：Newdata %*% rotation

2. 如何找对我们某个PC贡献最大或top10的维度？取绝对权重最大的top维度集合

在对RNA-seq数据进行PCA分析时非常实用，我们发现了感兴趣的PC，往往要找哪些基因贡献最大，或者直接可视化我们某个基因在前两个PC中的位置。

3. 如何在原数据里可视化我们的投射/旋转方法？

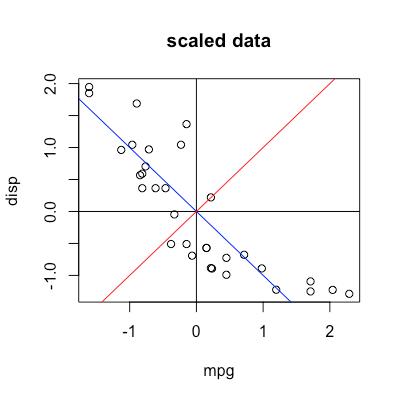
蓝线就代表了我们原坐标下的PC1方向，如何反向找出蓝线的斜率呢？

假设蓝线为y=kx，那么向量[1, k]在rotation的作用下必然变为[c, 0]，c的大小和符号是不确定的，但我们有一个确定的0，有点线性代数基础的就知道如何解k了。

plot(my_data, main = "scaled data")
abline(v=0)
abline(h=0)
abline(coef = c(0, -0.7071068/0.7071068), col="blue")
abline(coef = c(0, 0.7071068/0.7071068), col="red")

那么我们就知道了第一个方差最大的方向是y = -0.7071068/0.7071068 * x，第二个方差最大的就是y = 0.7071068/0.7071068.

普通实现

如何用普通方法，不用线性代数和矩阵来求呢？

先明确总方差这个概念：

单一维度的方差好理解，直接求var就行，比如我们scale后，mpg和disp的方差就都为1了。

但是我们的数据PCA之后，PC1的方差就为1.847425，PC2的方差为0.1524486。

Importance of components:
                          PC1     PC2
Standard deviation     1.3592 0.39045
Proportion of Variance 0.9238 0.07622
Cumulative Proportion  0.9238 1.00000

如何理解总方差呢？其实很简单，就是所有PC的方差之和。PC1的Proportion of Variance是这么算的：1.847425/(1.847425 + 0.1524486)

现在我们手动来做PCA，先求第一个PC，就是要找蓝线y = kx，如何求k？

我们要把所有点投射到蓝线上，然后要让所有的投影点的在蓝线这个维度方差最大化。

这里没办法了，点太多不可能手算，所以只能用最大似然估计了。

最大似然估计用的mle函数，此函数需要一个似然函数，变得就是A，就是Ax+By+C=0，我们就是不停地试A，然后看什么情况下我们所有的点在此线上投影的方差最大。

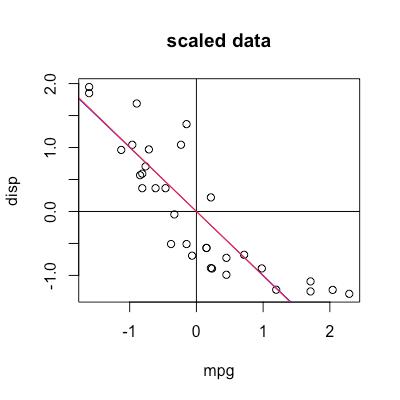
最后的结果是：1.009254*x + y = 0，可以看到与原来的线几乎重合，我们手动算出来的PC和prcomp算出来的一模一样。

这里的这个似然函数的构造有一点技巧：需要知道怎么算点到线的距离；根据勾股定理算投影长度，需要判断投影的正负。

PC1定了，其实PC2也就定了，因为只有一条线与PC1正交，就是垂直的线。所以也就不重复算了。

似然函数和最大似然估计不清楚的可以看我的这个文章：似然函数 | 最大似然估计 | likelihood | maximum likelihood estimation | R代码

##################
nll <- function(A) {
  # A=1
  B=1; C=0
  m <- my_data[,1]
  n <- my_data[,2]
  if (A!=0) {
    raw_sign <- as.integer(n > -m/A)
    raw_sign[raw_sign==0] <- -1
  } else {
    raw_sign <- 1
  }
  
  p <- sqrt(((A*m+B*n+C)^2 / (A^2 + B^2)) + m^2 + n^2) * raw_sign
  var(p)
}

est <- stats4::mle(minuslog=nll, start=list(A=1), )
summary(est)

plot(my_data, main = "scaled data")
abline(v=0)
abline(h=0)
abline(coef = c(0, -0.7071068/0.7071068), col="blue")
abline(coef = c(0, -1.009254), col="red")

参考：

Principal component analysis - wiki

Principal Component Analysis in R

主成分分析（Principal components analysis）-最大方差解释

PCA的线性代数实现

自此，我们已经了解了PCA的思想内涵，普通实现。

这个时候再来讲PCA的线性代数实现才是合适的，为什么线性代数里的工具能高效的实现PCA？

R的PCA包，prcomp和princomp，The function princomp() uses the spectral decomposition approach. The functions prcomp() and PCA()[FactoMineR] use the singular value decomposition (SVD).

待续~　　

2019年04月25日

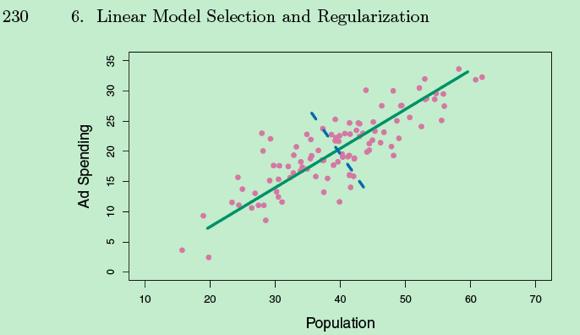
不该先说covariacne matrix协方差矩阵的，此乃后话，先从直觉理解PCA。先看一个数据实例，明显的两个维度之间有一个相关性，大部分的方差可以被斜对角的维度解释，少数的noise则被虚线解释。

我们的任务就是通过线性变化，找出一个维度能最大的解释数据的方差；然后继续找正交的第二个维度，直至最后一个正交维度。

不用矩阵思维我们都可以做，构造一个线性组合，优化方案就是方差最大，然后寻找另一个正交维度。

熟悉了普通解法，我们再来矩阵的解法。

PCA里最重要的就是covariacne matrix协方差矩阵，它完美的包含了我们需要的信息，变量内的方差，变量间的相关程度协方差；

我们想要干什么呢？我们的目的是将covariacne matrix对角化，也就是变量内的方差最大，变量间的相关程度协方差为0；

PCA的灵魂是什么？特征值和特征向量。Ax=λx. A是covariacne matrix，λ是特征值，x是特征向量。这个线性变化意味着什么呢？意味着在经过x处理（线性变换/移动）通过正交矩阵正交化后，A变成了特征值对角矩阵，也就是变量内的方差最大，变量间的相关程度协方差为0。这也解释了为什么covariacne matrix的特征值其实就是每个PC的variance。按variance排列也就自然而然了。同时也解释了为什么转化后的PC彼此线性无关，因为它是正交矩阵特征值构成的是对角矩阵。

特征向量的矩阵表征的就是线性变化，所以原先的数据矩阵在施加x运动后，会投射到新的PC里，这也从直觉上理解了PCA的精髓，线性投射。

PCA本身没有降维的功能，只是PCA告诉我们了每个PC的variance解释度，我们选取top 99%的PCs就能解释绝数据里的大部分信息，所以PCA才有了降维的功能！！！

大误区：没有明白特征向量的意义，搞混了特征向量、原数据矩阵和协方差矩阵之间的关系。没有完全理解对角化和行列式求解之间的联系。如何直观理解特征向量矩阵/投影矩阵的由来还是有点难度的！！！

矩阵特征值是对特征向量进行伸缩和旋转程度的度量，实数是只进行伸缩，虚数是只进行旋转，复数就是有伸缩有旋转。我们一般求得的是实数，所以特征值最大表示在这个方向的运动最大。

如何求实对称矩阵的特征值和特征向量？

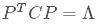
看来不把线性代数学通，想彻底搞懂PCA是不可能的了。

讲得人很多，但没有真正讲清楚的。从特征分解到协方差矩阵：详细剖析和实现PCA算法

求协方差矩阵的特征值和特征向量已经很明确了，但对角化的目的，以及为什么协方差矩阵的特征向量具有投影的功能没讲清楚。

协方差矩阵是实对称矩阵，不具有运动特性，所以不该从运动的角度去解释。

从定义出发，Ax=cx：A为矩阵，c为特征值，x为特征向量。矩阵A乘以x表示，对向量x进行一次转换（旋转或拉伸）（是一种线性转换），而该转换的效果为常数c乘以向量x（即只进行拉伸）。我们通常求特征值和特征向量即为求出该矩阵能使哪些向量（当然是特征向量）只发生拉伸，使其发生拉伸的程度如何（特征值大小）。这样做的意义在于，看清一个矩阵在那些方面能产生最大的效果（power），并根据所产生的每个特征向量（一般研究特征值最大的那几个）进行分类讨论与研究。知乎Rex

talia有个PPT讲得非常严谨。

不得不惊叹数学的神奇，一个复杂问题用这么精简巧妙的方式解决了。

对于基因表达（>30000 gene），表观（十万以上enhancer）等超多特征的数据，降维是绕不开的，尤其是在计算样本或细胞间的关系时，降维能有效的减少计算量。

降维的另一个作用就是可视化，所以分析单细胞数据总能见到PCA、t-SNE和diffusionMap。人最多可以看三维的数据，还得移动看，学术上严谨些，只用二维数据。

PCA，以基因表达数据为例，每个基因在样本间都是在变得，而且有很多是相互相关的，举个例子，如果两个/一群基因是完全相关的，那我们完全只需要一个变量/维度就可以解释样本里的所有变异。PCA就是通过线性变化，把原来的所有变量（n个）转化为新的n个PC，这些PC彼此间线性无关，而且可以根据变异的解释量来排序PC，每个变量对新的PC都有一个简单的线性转换公式。

PCA的数学基础：要有线性代数基础。PCA和SVD的联系。

问题：

1.为什么说PCA有降维的功能？明明线性变化后有与变量数相等的PC。

2.PCA适合给什么样的数据降维？什么情况下用其他降维方法会更好？

3.能不能把PCA的大致计算过程写下来？

4.PCA的应用，我有一个很感兴趣的维度，请把对该维度贡献最大的变量找出来；我有一个新的样品，能否给我一个新的PC打分

5.variance，如何理解特征向量表征了变异比例？

6.如何直观理解协方差，covariance？

7.PCA里是如何利用特征值和特征向量的？

8.如何理解“主成分分析就是把协方差矩阵做一个奇异值分解，求出最大的奇异值的特征方向”？

9.PCA和ICA有什么关系？

10.特征值和特征向量单独表示很好理解，如何写成对角矩阵形式？矩阵和向量基本运算要熟练。这里纠结了好久

11.PCA在图像压缩和图像识别方面也有应用。

12. 为什么特征向量的矩阵可以用于空间转换？

学习是一个思维发散和收敛的过程，不断深入，不断回归。

为了防止我又忘了我的目的，以下梳理一下我的任务：

1. 如何对RNA-seq的数据做PCA分析？

2. PCA原理；如何做到重新分配variance的？

3. 如何理解得到的PC；

4. 有个感兴趣的PC，如何提取出关键基因；

5. 如何把一个新的样本投射到已经建立的PCA坐标里，打分预测？

好了，开始发散，先到线性代数里走一圈。

PCA计算的起点是协方差矩阵，方差描述的是一群点偏离均值的程度（偏离度（平方）的均值/期望），标准差是方差的标准化，具有与原数据一样的单位/量纲。协方差描述的是两个变量之间的协同关系（两个变量与其各自均值的协变度），是相关性系数的前体（除以两个变量的标准差后就是相关性系数）。

协方差公式简单，但却有许多惊奇的特性，它居然可以描述两个变量的协同变化程度。协方差矩阵更是计算生物学的利器（协方差矩阵有什么意义？），很多工具分析的起点。

问题：为什么有了标准差还要方差，两者不是重复吗？为什么方差的度量选择了平方？为什么描述性统计的两个核心指标是均值和方差，而不是均值和标准差？参考链接，可导。

题外话：为什么样本的方差要除以n-1而不是n？参考链接：无偏估计。

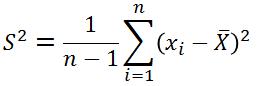
接下来就是求协方差矩阵covariance matrix的特征值和特征向量了eigenvalue and eigenvector。

直观理解，A就是我们的矩阵，它可以看作是运动，v是特征向量，特征值和特征向量表征的是一个矩阵的特征（如何理解矩阵特征值？），在可视化工具里，给定一个矩阵，我们可以找到它的一些特征值和特征向量，意思就是特征向量在运动后（乘以A），方向不变，长度变了，变化的长度就是λ。

线性代数就是解方程，前面解的方程是Ax=b，现在解的方程是Ax=λx.

说多了感觉脱离实际了，show me your code

需要注意的细节：scale会影响结果

head(mtcars)
res <- prcomp(mtcars, scale. = F, center = F, retx = T)
# res2 <- princomp(mtcars)
plot(res$x[,1:2])
res$x[1:5,1:5]
res$sdev

res$rotation[1:5,1:5]
recover <- as.matrix(mtcars) %*% as.matrix(res$rotation)
recover[1:5,1:5]

> head(mtcars)
                   mpg cyl disp  hp drat    wt  qsec vs am gear carb
Mazda RX4         21.0   6  160 110 3.90 2.620 16.46  0  1    4    4
Mazda RX4 Wag     21.0   6  160 110 3.90 2.875 17.02  0  1    4    4
Datsun 710        22.8   4  108  93 3.85 2.320 18.61  1  1    4    1
Hornet 4 Drive    21.4   6  258 110 3.08 3.215 19.44  1  0    3    1
Hornet Sportabout 18.7   8  360 175 3.15 3.440 17.02  0  0    3    2
Valiant           18.1   6  225 105 2.76 3.460 20.22  1  0    3    1

一般的主成分分析返回的信息有： sdev标准差，平方后就是每一个PC所能解释的方差，也就是特征向量；rotation对应了特征向量的矩阵；x就是最终的投射后的矩阵，就是原矩阵乘以特征向量rotation。

有个无法还原的就是Ax=λx，协方差矩阵乘以特征向量矩阵不等于右边，不知道哪里出错了。需要看下源码

PCA普林斯顿讲义

The Mathematics Behind Principal Component Analysis 数学基础，步骤很清楚，怎么做讲得很清楚，但没讲出缘由，为什么可以这么做

Principal Component Analysis in R: prcomp vs princomp R代码

Principal Component Analysis (PCA) - THE MATH YOU SHOULD KNOW! 数学部分完全不懂

Principal Components Analysis: Theory and Application to Gene Expression Data Analysis 正统paper

再谈协方差矩阵之主成分分析 - 传神的讲了协方差矩阵的神奇作用

如何理解主成分分析中的协方差矩阵的特征值的几何含义？

PCA的数学原理非常不错了

总结一下：做PCA，首先我们会构建特征/变量的协方差矩阵，然后求其特征值和特征向量，top特征向量构建的矩阵就能将原始数据投射到新的相互独立的且排好序的PC空间里。

新的问题：

1. 为什么这样就可以投射到新的PC了？特征向量可以理解为对原来的所有维度进行重构了，特征向量相当于是对应的线性权重，这就是PCA核心的线性变换过程。为什么特征向量就是权重，如何理解？

2. 为什么求解的特征值就是对应特征向量的方差，这些是怎么联系起来的？必须理解协方差矩阵的特征值和特征向量意味着什么！

深刻理解到，线性代数和概率论不学好，搞统计研究就会举步维艰。

Dimensionality reduction for visualizing single-cell data 需要总结一下

番外篇：

1. PCA与聚类的关系，PCA不是聚类，它只是降维，只是在RNA-seq当中，好的replicates往往会聚在一起，才会误以为PCA可以做聚类。PCA是降维，是聚类的准备工作，最常见的聚类是k-means聚类，为了降低计算复杂度，我们可以在PCA的结果里做聚类。

2. 协方差矩阵为什么比相关性矩阵用途更广？因为协方差里包含了两种信息，变量间的相关性以及变量内部的方差，相关性标准化后丢失了太多的信息，所以用得少了。

例子：以小学生基本生理属性为案例，分享下R语言的具体实现，分别选取身高（x1）、体重(x2)、胸围(x3)和坐高(x4)。具体如下：

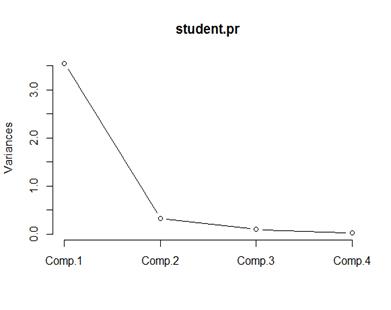
> student<- data.frame(  
+     x1=c(148,139,160,149,159,142,153,150,151),  
+     x2=c(41 ,34 , 49 ,36 ,45 ,31 ,43 ,43, 42),  
+     x3=c(72 ,71 , 77 ,67 ,80 ,66 ,76 ,77,77),  
+     x4=c(78 ,76 , 86 ,79 ,86 ,76 ,83 ,79 ,80)  
+ ) 
> student.pr <- princomp(student,cor=TRUE)
> summary(student.pr,loadings=TRUE)
Importance of components:
                         Comp.1     Comp.2     Comp.3      Comp.4
Standard deviation     1.884603 0.57380073 0.30944099 0.152548760
Proportion of Variance 0.887932 0.08231182 0.02393843 0.005817781
Cumulative Proportion  0.887932 0.97024379 0.99418222 1.000000000

Loadings:
   Comp.1 Comp.2 Comp.3 Comp.4
x1 -0.510  0.436 -0.139  0.728
x2 -0.513 -0.172 -0.741 -0.398
x3 -0.473 -0.761  0.396  0.201
x4 -0.504  0.448  0.524 -0.520
> screeplot(student.pr,type="lines")

standard deviation：标准差

Proportion of Variance：方差的占比

Cumulative Proportion：累计贡献率

由上图可见四项指标做分析后，给出了4个成分，他们的重要性分别为：0.887932、0.08231182、0.02393843、0.005817781，累积贡献为：0.887932、0.97024379、0.99418222 1.000000000各个成分的碎石图也如上，可见成份1和成份2的累积贡献已经达到95%，因此采用这两个成份便可充分解释学生的基本信息。

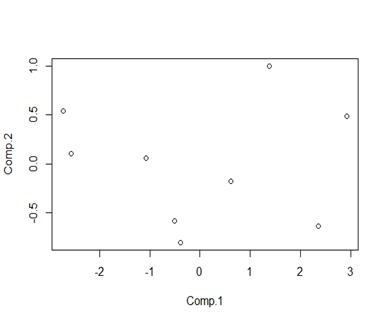
可以算出 Z1 和 Z2的公式

> temp<-predict(student.pr) 
> plot(temp[,1:2])

参考链接：R语言与数据分析之五：主成分分析（还有很多系列，慢慢看）

主成分分析（Principal Component Analysis，PCA）的目标是用一组较少的不相关的变量代替大量相关变量，同时尽可能保留原始变量的信息，推导所得的变量就成为主成分，是原始变量的线性组合。也就是将N个变量（N维），通过线性组合，降维到K个综合变量（K维，K <N）来归纳性解释某一个现象。

先举个简单例子帮助理解吧：

某篮球俱乐部有40名男同学，同学之间各个指标存在或大或小的差异，包括身高、体重、视力、百米速度、肺活量、每天练球时长、睡眠时间等指标。在季度选拔中，40名同学进球得分数（成绩）存在差异，那么这些指标是否均与成绩相关？或者相关性有多大？

此时可能就要用到PCA，分析方法简述如下：

1选择初始变量

比如以上7个指标作为变量（a1 - a7），40名同学作为样本。

2对原始数据矩阵进行标准化，做相关系数矩阵

（1）原始数据矩阵：每行为40名男同学的各项指标值，每列为各项指标在40名同学中的体现；

（2）因为各个指标度量单位不同，取值范围不同，不宜直接由协方差矩阵出发，因此选择相关系数矩阵。

3计算特征值及相应特征向量

4判断主成分的个数

最常见的方式是根据特征值判断，一般选择特征值大于1的变量数作为PC个数，假如，此项分析中特征值大于1的有两个，则最终可以有2个主成分（具体主成分个数可以根据实际研究调整）。

5得到主成分表达式

通过分析得到第一主成分（PC1）和第二主成分（PC2），假设表达式如：（a1*表示a1标准化后的数值）

6结合数据的实际意义开展分析

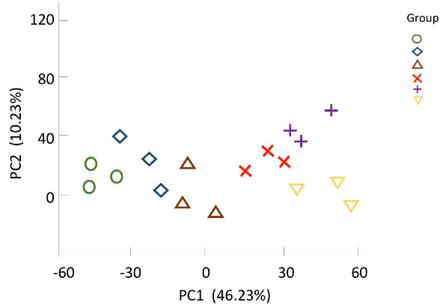
PC1比PC2更能解释样本间差异的原因（如下图中横纵轴的百分比）。PC1的线性组合中a1、a2、a3、a6贡献度较大（前面的系数较大），PC2的线性组合中a5贡献度较大。以PC1为横轴，各个样本根据成绩大小有明显区分，说明以上7个指标中，身高、体重、视力、每天练球时长这4个指标与同学的成绩相关性更强。为了迎合线性组合的概念，应该找个更合适的词语来综合描述身高、体重、视力、每天练球时间这4个指标，以涵盖这4个指标的意义。理解了以上的概念，再将主成分分析用于RNA-seq也很容易理解。