零知识证明|2.什么是多项式盲计算？

Posted 2022-11-25 TurkeyCock

上一篇介绍了什么是同态隐藏。假设取$E(x)=g^x$，则$E(x+y)$可以通过$E(x)$和$E(y)$计算出来：

$E(x+y)=E(x)\cdot E(y)$

实际上，不仅仅支持加法，支持所有"线性组合"的同态隐藏，比如$E(ax+by)$：

$E(ax+by)=g^{ax+by}=g^{ax}\cdot g^{by}=(g^x{)}^a\cdot (g^y{)}^b=E(x{)}^a\cdot E(y{)}^b$

需要注意的是，上面的加法和乘法运算都是模p运算。

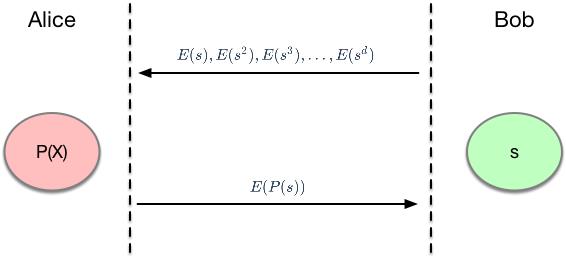
假设现在有一个d次多项式$P(X)=a_0+a_1\cdot X+a_2\cdot X^2+\dots +a_d\cdot X^d$，其中的系数$a_0,\dots ,a_d\in 0,p-1$是Alice需要保护的秘密。根据上面的特性，我们可以计算出$E(P(X))$：

$E(P(X))=E(1{)}^{a_0}\cdot E(X{)}^{a_1}\cdot E(X^2{)}^{a_2}\dots \cdot E(X^d{)}^{a_d}$

现在Bob想来验证Alice是不是真的知道这些秘密，于是他决定随机指定一个数$s$，要求Alice计算$E(P(s))$等于多少。但是，Bob不想直接把$s$的值告诉Alice，也就是说，这个$s$是Bob的秘密。显然，这又需要一次同态隐藏，也就是说，Bob把下面这些值提供给Alice：

$E(s),E(s^2),E(s^3),\dots ,E(s^d)$

然后Alice就可以根据上面的公式计算$E(P(s))$的值：

$E(P(s))=E(1{)}^{a_0}\cdot E(s{)}^{a_1}\cdot E(s^2{)}^{a_2}\dots \cdot E(s^d{)}^{a_d}$

最终的效果是：在Bob不知道P(X)中的系数是多少，而Alice也不知道s等于多少的情况下，完成多项式的验证。这就是所谓的"多项式盲计算"。

下面举个例子来加深理解，假设$P(X)=1+2X+3X^2,E(x)=3^x,p=7$：

Bob想验证$s=2$这一点上的$E(P(s))$的值，那么他需要提供这2个值：$E(s)=2,E(s^2)=4$

然后Alice根据这3个值计算$E(P(s))$的值然后返回给Bob：

$E(P(s))=E(1{)}^1\cdot E(s{)}^2\cdot E(s^2{)}^3=3\cdot 4\cdot 64{|}_{mod7}=768{|}_{以上是关于零知识证明|2.什么是多项式盲计算？的主要内容，如果未能解决你的问题，请参考以下文章}$

零知识证明|3.什么是KCA系数知识假设？

零知识证明|3.什么是KCA系数知识假设？

零知识证明|4.如何验证多项式盲计算的值？

零知识证明|4.如何验证多项式盲计算的值？

安全多方计算 同态密文计算 零知识证明 是什么对比优缺点

零知识证明|1.什么是同态隐藏？