数据结构与算法(Python)——常见数据结构Part5(二叉搜索树BST和AVL)
Posted The fool
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构与算法(Python)——常见数据结构Part5(二叉搜索树BST和AVL)相关的知识,希望对你有一定的参考价值。
写在前面
在上一节part4我们熟悉了二叉树结构,以及其遍历算法,本节将继续学习常见的树结构,包括二叉搜索树和一种自平衡的二叉搜索树AVL。
1. 二叉搜索树
二叉搜索树(Binary Search Tree):二叉查找树,也称二叉搜索树、有序二叉树(ordered binary tree),排序二叉树(sorted binary tree)。它或者是一棵空树;或者是指具有如下性质的二叉树:
(1)若它的左子树不为空,则左子树上所有的节点的值均小于它的根节点的值 (2) 若它的右子树不为空,则右子树上所有结点的值均大于它的根结点的值(3) 它的左、右子树也分别为二叉搜索树。
上面的定义是一种递归定义,例如下图所示为一棵BST:
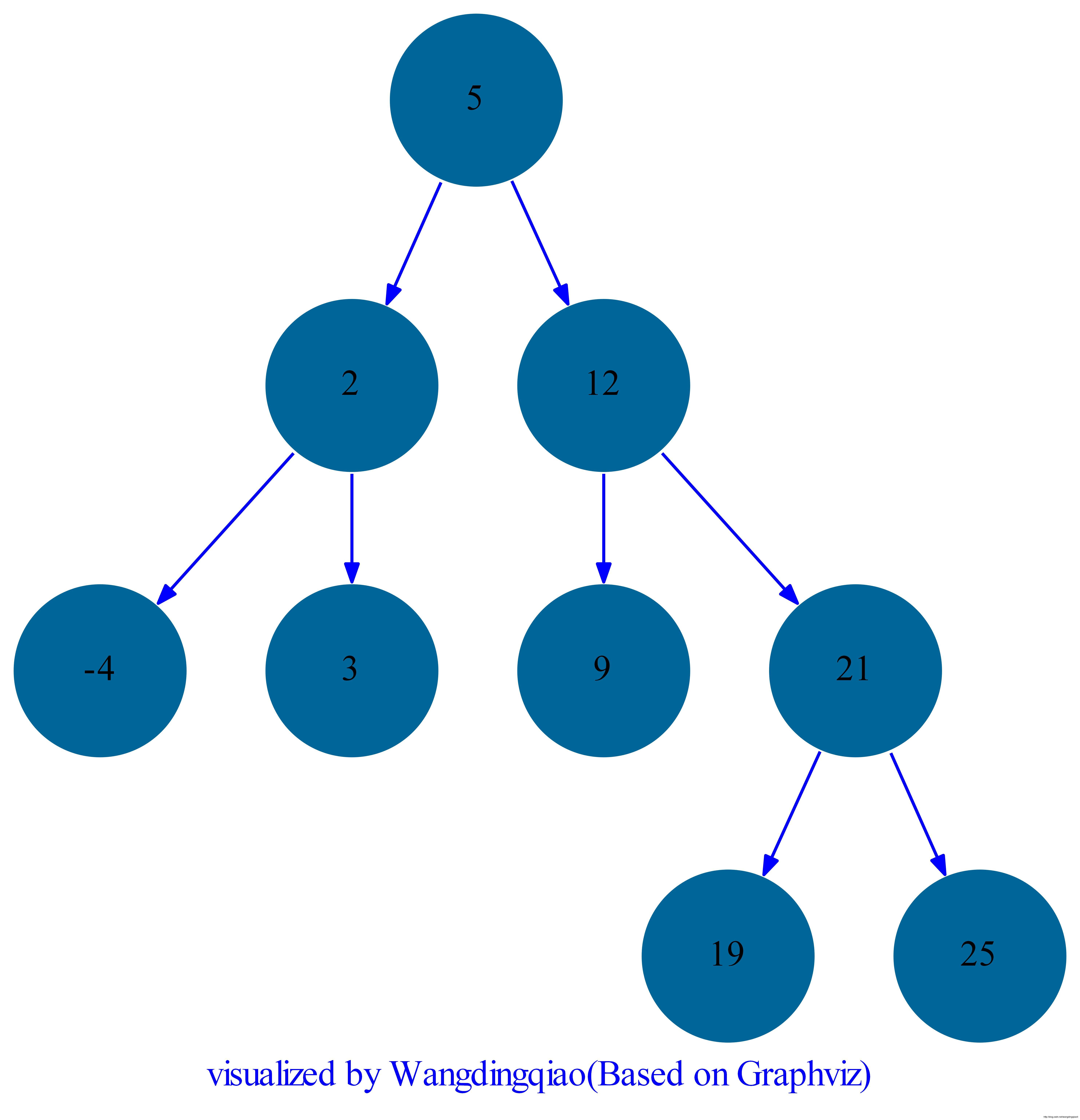
定义二叉搜索树如下:
class BinarySearchTree(BinaryTree):
"""
二叉搜索树
"""
def __init__(self):
self.root = None1.1 插入操作
插入二叉树时,插入元素需要与树中已有元素对比,插入到合适位置,以保持二叉树的特性,这个过程可以看做是一个递归的过程,插入元素为e, 插入节点从树的根节点开始,这一过程描述为:
case 1: e如果比当前节点大,则与当前节点的右孩子的根节点比较,即当前节点右孩子设为当前节点,继续比较;
case 2: e如果比当前节点小,则与当前节点的左孩子的根节点比较,即当前节点左孩子设为当前节点,继续比较;
case 3: e如果与当前节点相等,则不插入。
这个过程即可使用迭代实现,也可以递归实现,一般采用递归比较简洁,描述为:
def add(self, value):
if not self.root:
self.root = TreeNode(value)
return True
else:
return BinarySearchTree.__add_value(self.root, value)
@staticmethod
def __add_value(node, value):
if not node:
return False
if node.data == value:
return False # duplicate
elif value < node.data:
if node.left:
return BinarySearchTree.__add_value(node.left, value)
else:
node.left = TreeNode(value)
else:
if node.right:
return BinarySearchTree.__add_value(node.right, value)
else:
node.right = TreeNode(value)
return True例如初始树为(图片来自:Binary search tree. Adding a value):

插入元素4的过程为:

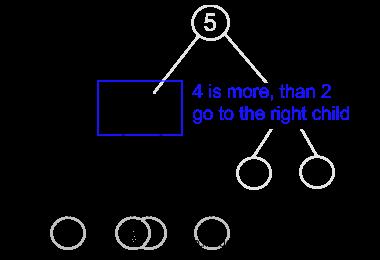
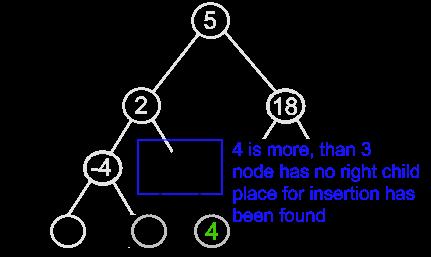

1.2 查找操作
实际上上面的插入过程,已经包含了查找过程,只是插入时需要查找到合适位置,而查找则只是查找元素位置。这一过程描述为:
def find(self, value):
return BinarySearchTree.__find__(self.root, value)
@staticmethod
def __find__(node, value):
if not node:
return False
if value == node.data:
return True
elif value < node.data:
return BinarySearchTree.__find__(node.left, value)
else:
return BinarySearchTree.__find__(node.right, value)1.3 删除操作
二叉搜索树的删除操作的一个难点在于始终要保持二叉树的性质不被破坏,因此需要分情况进行讨论。
case 1: 被删除节点没有孩子节点,例如下面树中删除节点-4。
这个时候的操作仅需要将这个被删除节点的父节点相应孩子指针域置位None即可。
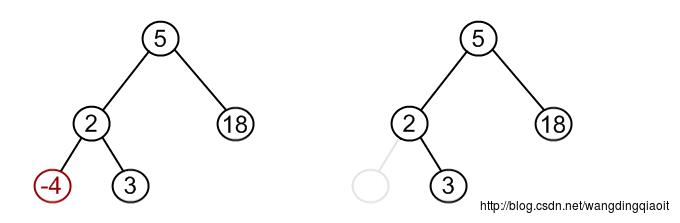
case 2: 被删除节点有一个孩子节点,例如下面树中删除节点18。
这种情形,只需要将被删除节点的孩子指针域连接到这个被删除的节点的那个孩子即可,过程如下图所示:

case 3: 被删除节点有两个孩子节点。
这种情形要比上面两种情况复杂,因为不能简单地将被删除节点的父节点孩子指针域指向其中任何一个剩余的孩子。例如下图删除12。这个时候有两种策略,其中一个策略叫做复制删除(remove by copy)。
复制删除的思想是: 寻找待删除节点p的直接后继节点(前驱节点也可以,是一个对称的操作),将后继节点的值复制到p中,然后删除这个后继节点(后继节点就是p的右子树中根节点的最左边孩子结点,这个节点最多只有一个孩子,因此转换为case1和case2的情况)。例如下面删除12的时候,寻找12的后继节点19,执行复制删除的过程如下所示:
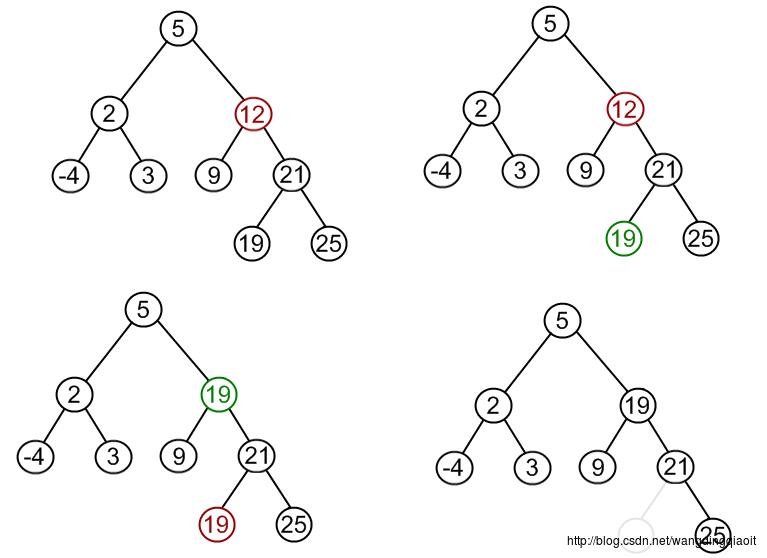
我们将删除三种情况,整理一下,得出BST的删除操作算法描述为:
case 1: 对于没有孩子的结点,直接删除即可
case 2: 对于只有一个孩子的结点,直接把孩子替换待删除结点即可
case 3: 对于两个孩子都不为空的结点p,复制的思想即为:
寻找待删除节点p的直接后继节点(前驱节点也可以,是一个对称的操作),将后继节点的值复制到p中,然后删除这个后继节点(后继节点就是p的右子树中根节点的最左边孩子结点,这个节点最多只有一个孩子,因此转换为case1和case2的情况)。
用python实现上述算法,表达为:
def remove_by_recursion(self, value):
if not self.root:
return False
elif value == self.root.data:
temp_root = TreeNode() # 创建一个临时节点 方便处理
temp_root.left = self.root
ret = BinarySearchTree.__remove__(temp_root.left, temp_root, value)
self.root = temp_root.left
return ret
elif value < self.root.data and self.root.left:
return BinarySearchTree.__remove__(self.root.left, self.root, value)
elif value > self.root.data and self.root.right:
return BinarySearchTree.__remove__(self.root.right, self.root, value)
return False
@staticmethod
def __remove__(node, parent_node, value):
if not node or not parent_node:
return False
if value == node.data:
if node.left and node.right: # case 被删除节点左右孩子都存在
min_node = node.right
while min_node.left:
min_node = min_node.left
node.data = min_node.data
BinarySearchTree.__remove__(node.right, node, node.data)
else: # case 最多只有一个孩子存在
if node == parent_node.left:
parent_node.left = node.left or node.right
else:
parent_node.right = node.left or node.right
elif value < node.data and node.left:
return BinarySearchTree.__remove__(node.left, node, value)
elif value > node.data and node.right:
return BinarySearchTree.__remove__(node.right, node, value)
return False注意,在上面实现过程中, 当删除节点为根节点时,我们创建了一个临时节点,并以这个节点为真实根节点的父节点,然后执行删除操作,这种方式帮我们统一了代码流程,起到了简化处理的作用,否则针对删除根节点要做特殊处理,代码看起来混乱。
除了复制删除外,还有一种合并删除方法(remove by merging)。合并删除的思想,与复制删除的不同之处主要体现在case3的处理上。case3时,合并删除,将删除节点p的右子树重新合并到前驱的右子树上(前驱节点也即p的左子树根节点的最右边孩子结点,它无右孩子,因此将p的右子树合并到这个前驱结点的右子树上),结点p的左孩子的根成为新的根结点(将p的左子树链接到p的后继的左子树上,是一个对称的操作,这种方法也是可以的)。例如下图,删除节点20的过程:
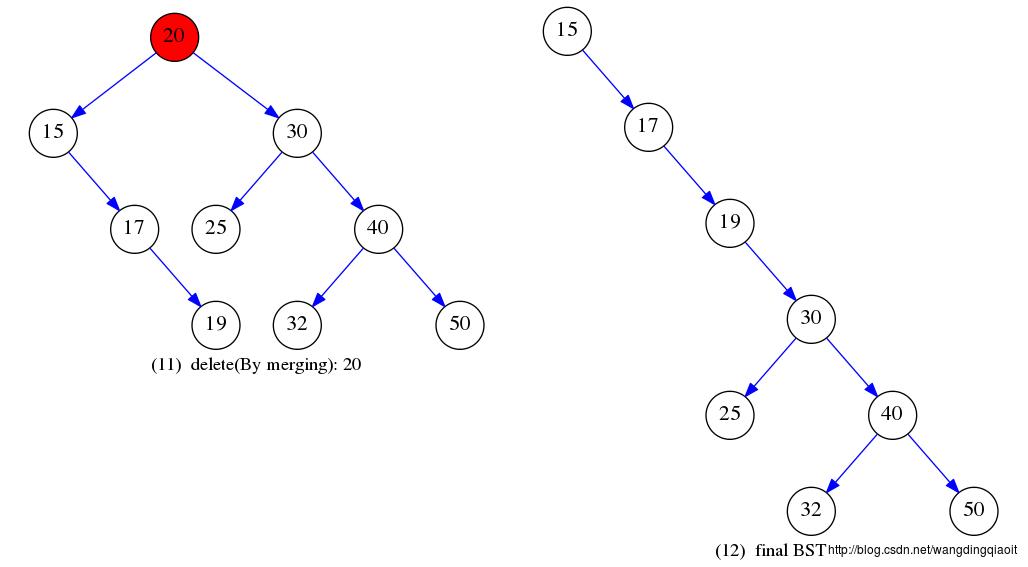
合并删除算法在下一部分介绍的AVL树中用的少,这里就不提供实现了,感兴趣地可以自行实现。
2.自平衡的二叉搜索树
2.1 why 平衡二叉搜索树
含有n个节点的二叉搜索树,其树形并不唯一确定,随着元素输入顺序以及删除操作的变化,树形会大有不同。例如下图表示了数据相同,但树形差别很大的两个BST。
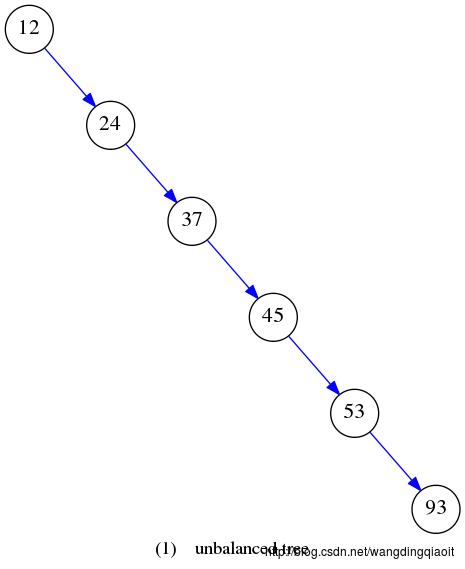
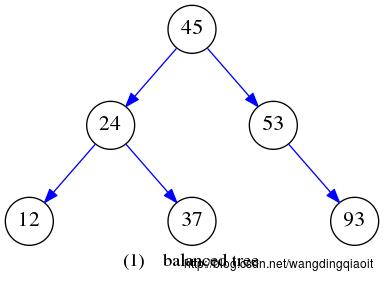
含有n个节点的二叉搜索树其平均查找长度和树的形态有关。对比上述两个BST,假设访问其中每个元素的概率相同,则第一个BST中查找长度的期望为14/6,而第二个BST的查找长度的期望为21/6。
最坏的情况,即第一个BST所示的单支树情况,查找的时间复杂度为O(n),而我们希望保持二叉搜索树深度较小,当二叉搜索树平衡时(平衡也就是树的所有叶子节点都出现在一个或者两个层次上,每个节点左子树与右子树的深度之差的绝对值不大于1)平均查找时间复杂度为O(logn)。
当n=10000时,最坏需要查找10000次,而将10000个点存储在完全平衡的二叉搜索树中,树的高度为floor(log2(10000))+1=14,则最多需要查找14次。这个差别还是很大的。
因此要尽可能保持树的平衡。保持树的平衡,有两种策略,一种是全局的,即当插入和删除操作完毕后,对树进行重建,全局调整树为平衡树, 这类算法包括DSW平衡算法;另一种是局部调整,即当插入或者删除导致树不平衡时就立即在局部范围内调整,使树保持平衡,这种树称之为自平衡二叉搜索树(Self-balancing binary search tree),典型地如AVL树、红黑树,本节我们重点学习AVL树。
2.2 AVL树的定义
AVL树的名字以3个发明者名字(Adelson-Velsky and Landis)首字母缩写构成,在AVL中节点N的平衡因子(Balance factor)定义为:
BalanceFactor(N):=Height(RightSubtree(N))–Height(LeftSubtree(N)) B a l a n c e F a c t o r ( N ) := H e i g h t ( R i g h t S u b t r e e ( N ) ) – H e i g h t ( L e f t S u b t r e e ( N ) )
注意: 有些教材或者教程,定义平衡因子为左子树高度减去右子树高度,这个做法对于维护树的平衡没有影响,只要在失去平衡时做对应调整即可。
平衡因子的取值范围为:
BalanceFactor(N)∈–1,0,+1 B a l a n c e F a c t o r ( N ) ∈ – 1 , 0 , + 1 。
这个取值范围表明: 对于AVL树中任何一个节点N,其左右子树的高度差绝对值最大为1。对于一个节点N,如果bf <0 则表示节点N的左子树比右子树高;而 bf > 0 则表示节点N的右子树比左子树高。当bf=0时,则说明左子树和右子树等高。下图是标记了平衡因子的一棵AVL:
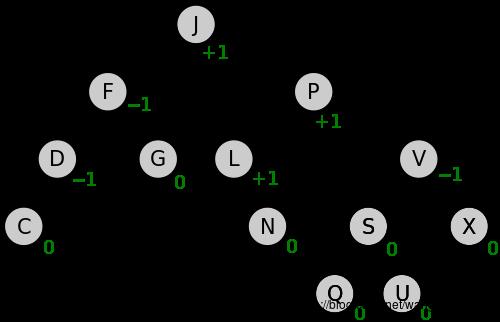
下图是AVL和非AVL的一个对比:
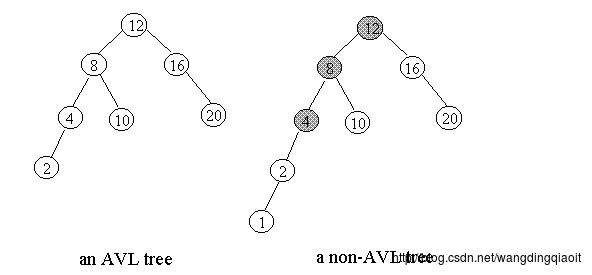
如何定义AVL树的节点呢? 不同的教材或者教程,不同语言,给出了不同定义,例如版本1:
class AVLNode(object):
"""A node in the AVL tree."""
def __init__(self, parent, k):
"""Creates a node.
Args:
parent: The node's parent.
k: key of the node.
"""
self.key = k
self.parent = parent
self.left = None
self.right = None版本2:
class Node():
def __init__(self, key):
self.key = key
self.parent = None
self.leftChild = None
self.rightChild = None
self.height = 0各种不同版本定义不尽相同, 这里需要注意一点是: 使用平衡因子来确定AVL节点平衡,比使用高度来维护AVL节点平衡,代价要小,使用高度时很可能进行了不必要的高度计算,从而影响算法效率。 当然,采用平衡因子的实现则相对要复杂多了,维护平衡因子的工作比计算节点的高度更难以控制。
我们定义的版本如下:
class AVLTreeNode(object):
"""
树节点
"""
LEFT_HIGHER = -1
EQUAL_HEIGHT = 0
RIGHT_HIGHER = 1
def __init__(self, data, left=None,
right=None, parent=None, bf=0):
self.data = data
self.left, self.right = left, right
self.parent = parent
self.bf = bf
def __str__(self):
return str(self.data) + "bf(" + str(self.bf) + ")"
def __repr__(self):
return self.__str__()2.3 AVL调整的基本操作
在AVL上进行插入或者删除操作后,可能引起插入节点到根节点路径上某个节点失去平衡。这个时候为了维持AVL的特性,即任意节点的左右子树高度差绝对值最大为1,我们需要根据不同情况,进行相应地调整。定义4个基本的调整操作如下。
case 1: LL类型,只需要一次右旋转调整即可。
T1, T2, T3 and T4 are subtrees.
z y
/ \\ / \\
y T4 Right Rotate (z) x z
/ \\ - - - - - - - - -> / \\ / \\
x T3 T1 T2 T3 T4
/ \\
T1 T2根据上面的节点定义,我们实现为:
def right_rotate(self, node):
"""
右旋转调整节点node
p q
/ \\ / \\
q s => ql p
/ \\ / \\
ql qr qr s
:param node: 待调整节点
:return: None
"""
if not node or not node.left:
raise AssertionError(
" right rotate to illegal node " + str(node))
parent_node = node.parent
node_left = node.left
node.left = node_left.right
if node.left:
node.left.parent = node
node_left.right = node
node.parent = node_left
if parent_node:
if node == parent_node.left:
parent_node.left = node_left
else:
parent_node.right = node_left
node_left.parent = parent_node
else:
self.root = node_left
node_left.parent = None上面实现中需要注意的是,因为需要引入了节点的parent指针,因此在旋转过程中也需要维护这个指针,如果忽略了这一点将造成程序错误。可以看出引入parent指针,也增加了实现的复杂性。作为一个具体的例子,依次插入节点3,2,1,调整如下图所示:
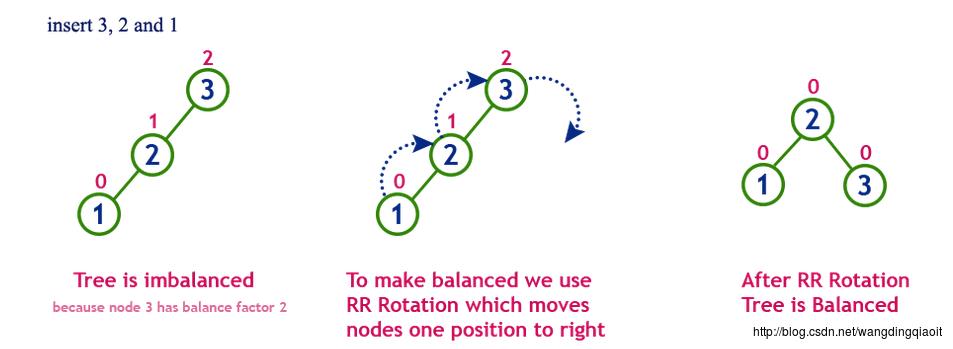
case 2: RR类型,只需要一次左旋转调整。
z y
/ \\ / \\
T1 y Left Rotate(z) z x
/ \\ - - - - - - - -> / \\ / \\
T2 x T1 T2 T3 T4
/ \\
T3 T4右旋转的实现和左旋转类似,实现代码在此略去。
case 3 : LR类型,先进行左旋转,然后进行一次右旋转。
z z x
/ \\ / \\ / \\
y T4 Left Rotate (y) x T4 Right Rotate(z) y z
/ \\ - - - - - - - - -> / \\ - - - - - - - -> / \\ / \\
T1 x y T3 T1 T2 T3 T4
/ \\ / \\
T2 T3 T1 T2这个情况相比之前情况,显得复杂一些,需要注意的是:进行两次旋转的作用节点并不是同一个,进行左旋转时支点是失去平衡的节点z的左孩子节点y,进行右旋转时支点是失去平衡的节点z。
对应的python实现为:
def left_right_rotate(self, node):
"""
先左旋转 然后右旋转调整节点node
:param node: 待调整节点
:return: None
"""
self.left_rotate(node.left)
self.right_rotate(node)一个具体的例子,例如依次插入节点3,1,2,调整如下图所示:
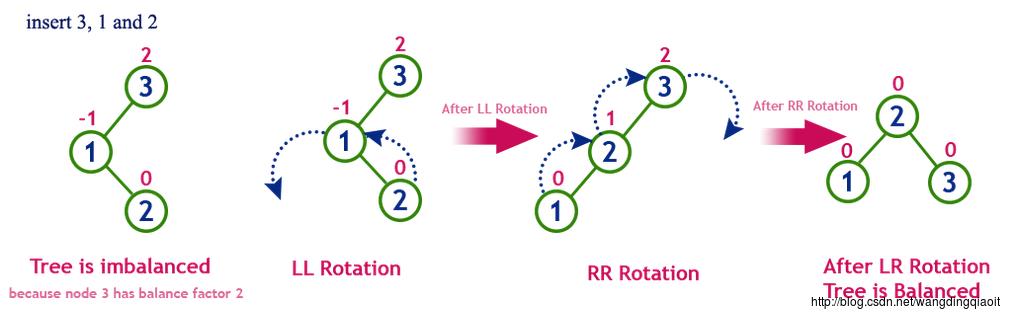
case 4: RL类型,先进行一次右旋转,然后进行一次左旋转。
z z x
/ \\ / \\ / \\
T1 y Right Rotate (y) T1 x Left Rotate(z) z y
/ \\ - - - - - - - - -> / \\ - - - - - - - -> / \\ / \\
x T4 T2 y T1 T2 T3 T4
/ \\ / \\
T2 T3 T3 T42.4 AVL的插入操作
插入操作的过程包括两个阶段:
1) 根据插入元素,找到插入位置,插入元素,这个过程和普通BST一样。
2) 更新插入节点的父节点到根节点路径上的节点的平衡因子,如果某个节点失去平衡,则需要进行调整。
插入一个新节点,改变的是从这个节点的父节点到根节点路径上节点的平衡因子,只有这条路径上的节点才会出现不平衡现象。如下图所示(来自AVL-insert):
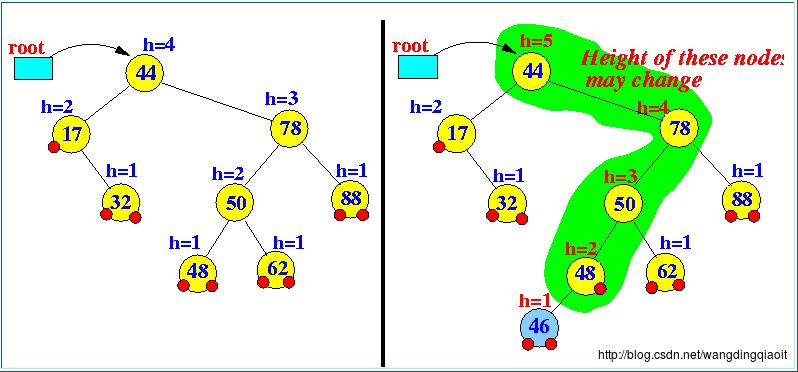
在上图中左边AVL插入节点46,影响的绿色部分表示的路径上节点的高度,我们需要调整的也是这条路径上节点的平衡因子。
这里需要注意的一个关键问题是: 什么时候停止更新节点平衡因子? 如果遇到一个节点,在插入新节点后高度不变,则可以停止更新了,因为它的祖先节点都没有受到影响。这样,我们需要一个布尔变量标志taller来记录树的高度是否发生了变化。
在python中要改变函数传递的对象,这个对象必须是可变对象(参见python快速入门篇1),而内置的bool变量时不可变的,因此我们自己封装一个可变布尔对象,如下:
class BoolObject(object):
"""
可变布尔对象
"""
def __init__(self, status=False):
self.status = status
def set_status(self, status):
self.status = status
def get_status(self):
return self.status
def __str__(self):
return (self.status and 'True') or 'False'
def __repr__(self):
return self.__str__()在插入节点时,先考虑插入当前节点左孩子的情况。一共细分为4种情况,假设插入节点为X,则调整过程如下所示:
case 1: 插入之前A平衡因子已经为-1了,再次插入A左子树,同时是B节点平衡因子变为-1,则A失去平衡,属于LL类型,需要右旋转处理。
A B
/ \\ / \\
B C(h) right rotate(A) / \\
/ \\ ================> D(h) A
/ \\ | / \\
D(h) E X E C(h)
|
Xcase 2: 插入前A平衡因子为-1,再次插入A的左子树,这次B的平衡因子变为+1,属于LR类型,但是对于节点E的平衡因子需要进行讨论,因此一共包括3中细分情况,如下:
case 2a: 插入后E节点平衡因子为-1。
A A E
/ \\ / \\ / \\
/ \\ / \\ / \\
B C(h) left rotate(B) E C right rotate(A) B A
/ \\ ================> / \\ ================> / \\ / \\
/ \\ / \\ / \\ / \\
D E B G D F G C
/ \\ / \\ |
F G(h-1) D F X
| |
X X
case 2b: 插入后E平衡因子为+1。
A A E
/ \\ / \\ / \\
/ \\ / \\ / \\
B C(h) left rotate(B) E C right rotate(A) B A
/ \\ ================> / \\ ================> / \\ / \\
/ \\ / \\ / \\ / \\
D E B G D F G C
/ \\ / \\ | |
F G(h-1) D F X X
|
X case 3c: 插入后E的平衡因子为0。
A A E
/ / / \\
B left roate(B) E right rotate(A) / \\
\\ ================> / ================> B A
E B上面情况,总结如下表所示:
| 旋转之前 | 旋转类型 | 旋转之后 |
|---|---|---|
| A=-2, B=-1 | 一次右旋转 | A=0, B= 0 |
| A=-2, B=+1, E=-1 | 先左旋转,后右旋转 | A=+1, B=0, E=0 |
| A=-2, B=+1, E=+1 | 先左旋转,后右旋转 | A=0, B=-1, E=0 |
| A=-2, B=+1, E=0 | 先左旋转,后右旋转 | A=0, B=0, E=0 |
对于插入当前节点右孩子的情况,也有类似讨论,限于篇幅,这里略去,留给读者自行练习。总结上述过程,插入节点部分实现为:
def __add_value__(self, node, value, taller):
result = True
if not node:
result = False
elif node.data == value:
result = False # duplicate
elif value < node.data:
if node.left:
result = self.__add_value__(node.left, value, taller)
else:
node.left = AVLTreeNode(value, parent=node)
taller.set_status(True)
if result and taller.get_status():
if node.bf == AVLTreeNode.LEFT_HIGHER: # 在左子树插入前已经左边高则需要平衡处理
self.left_balance(node)
taller.set_status(False)
elif node.bf == AVLTreeNode.EQUAL_HEIGHT: # 在左子树插入前节点平衡则现在左边变高
node.bf = AVLTreeNode.LEFT_HIGHER
else:
node.bf = AVLTreeNode.EQUAL_HEIGHT # 在左子树插入前节点右边高则现在平衡了
taller.set_status(False)
else:
if node.right:
result = self.__add_value__(node.right, value, taller)
else:
node.right = AVLTreeNode(value, parent=node)
taller.set_status(True)
if result and taller.get_status():
if node.bf == AVLTreeNode.LEFT_HIGHER: # 插入右子树前节点左边高则现在平衡了
node.bf = AVLTreeNode.EQUAL_HEIGHT
taller.set_status(False)
elif node.bf == AVLTreeNode.EQUAL_HEIGHT: # 插入右子树前节点平衡则现在右边高了
node.bf = AVLTreeNode.RIGHT_HIGHER
else: # 插入右子树前节点已经右边高了则需要平衡处理
self.right_balance(node)
taller.set_status(False)
return result上面分析的插入当前节点左孩子,而进行的左平衡处理过程,实现为:
def left_balance(self, node):
"""
左平衡处理
:param node: 待处理节点
:return: None
"""
if not node or not node.left:
raise AssertionError(" left balance to illegal node " + str(node))
left_node = node.left
if left_node.bf == AVLTreeNode.LEFT_HIGHER: # LL型 右旋转
node.bf = AVLTreeNode.EQUAL_HEIGHT
left_node.bf = AVLTreeNode.EQUAL_HEIGHT
self.right_rotate(node)
elif left_node.bf == AVLTreeNode.RIGHT_HIGHER: # LR型 先左旋转 后右旋转
left_node_right = left_node.right
if left_node_right.bf == AVLTreeNode.LEFT_HIGHER:
node.bf = AVLTreeNode.RIGHT_HIGHER
left_node.bf = AVLTreeNode.EQUAL_HEIGHT
elif left_node_right.bf == AVLTreeNode.RIGHT_HIGHER:
node.bf = AVLTreeNode.EQUAL_HEIGHT
left_node.bf = AVLTreeNode.LEFT_HIGHER
else:
node.bf = AVLTreeNode.EQUAL_HEIGHT
left_node.bf = AVLTreeNode.EQUAL_HEIGHT
left_node_right.bf = AVLTreeNode.EQUAL_HEIGHT
self.left_rotate(left_node)
self.right_rotate(node)
else:
raise AssertionError(" logic error , should not left balance node " + str(node))2.5 一个完整的插入示例
插入元素序列为 50, 25, 10, 5, 7, 3, 30, 20, 8, 15 ,过程如下图所示(来自AVL Trees ):

2.6 AVL删除操作
删除操作也包括两个步骤:
1)以BST方式删除节点,使用复制删除方法,将删除节点归一化为删除最多只有一个孩子的情况。
2)调整删除节点父节点到根节点路径上节点的平衡因子,如果节点失去平衡则进行调整。
调整过程和插入时很类似,但是仍然要注意一个关键问题: 什么时候停止调整? 停止条件是当删除节点对当前节点的高度没有影响时停止,与插入节点不同,这种调整可能超过一次。如下图所示:

b图中删除了节点80,需要调整节点75,调整完毕后,节点50出现不平衡,仍然需要继续调整。我们同样设置一个布尔变量shorter来保存树高度变化的情况,当删除节点x后根据情况设置shorter变量,当shorter=false时则说明可以停止更新节点平衡因子了。
2.6.1 删除节点的过程
删除节点的完整算法原文描述为:(来自Height Balance: AVL Trees):
- Reduce the problem to the case when the node x to be removed has at most one child.
- Delete x. We use a bool variable shorter to show if the height of a subtree has been shortened.
- While shorter is true do the following steps for each node P on the path from the
parent of x to the root of the tree. When shorter becomes false, the algorithm terminates.
Case 1: Node P has balance factor equal. The balance factor of P is changed according
as its left or right subtree has been shortened, and shorter becomes false.
Case 2: The balance factor of P is not equal, and the taller subtree was shortened.
Change the balance factor of P to equal, and leave shorter as true.
Case 3: The balance factor of P is not equal, and the shorter subtree was shortened.
Apply a rotation as follows to restore balance. Let Q be the root of the taller subtree of P.
Case 3a: The balance factor of Q is equal. A single rotation restores balance, and shorter becomes false.
Case 3b: The balance factor of Q is the same as that of P.
Apply a single rotation, set the balance factors of P and Q to equal, and leave shorter as true.
Case 3c: The balance factors of P and Q are opposite. Apply a double rotation (first around Q, then around P),
set the balance factor of the new root to equal and the other balance factors as appropriate, and leave shorter as true.
也就是:
1. 将问题归一化为,删除x节点时,它最多只有一个孩子节点。
2.删除x。使用一个布尔变量shorter来记录子树的高度是否变低了。
3. 当shorter为true时,对x的父节点到根节点路径上的节点P执行下列步骤;当shorter变为false时,算法终止。
case 1: 节点P的平衡因子为0。节点P的左子树或者右子树高度被降低,这时shorter设置为false。
case 2: P的平衡因子不为0,并且较高的子树高度降低了,这时将P的平衡因子置为0,让shorter保持为true。
case 3: P的平衡因子不为0,并且较矮的子树高度降低了,这个时候需要进行旋转调整。设P的较高子树的根节点为Q。
case 3