[Python人工智能] 三十八.Keras构建无监督学习Autoencoder模型及MNIST聚类可视化详解

Posted Eastmount

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了[Python人工智能] 三十八.Keras构建无监督学习Autoencoder模型及MNIST聚类可视化详解相关的知识，希望对你有一定的参考价值。

从本专栏开始，作者正式研究Python深度学习、神经网络及人工智能相关知识。前一篇文章详细讲解了基于Transformer的商品评论情感分析案例。本篇文章将分享无监督学习Autoencoder的原理知识，然后介绍Keras构建自编码的案例，即通过MNIST手写数字案例进行对比实验及聚类分析，运行效果如下图所示。基础性文章，希望对您有所帮助！

本专栏主要结合作者之前的博客、AI经验和莫烦老师的视频（强推"莫烦大神"视频）及论文介绍，后面随着深入会讲解更多的Python人工智能案例及应用。基础性文章，希望对您有所帮助，如果文章中存在错误或不足之处，还请海涵！作者作为人工智能的菜鸟，希望大家能与我在这一笔一划的博客中成长起来。写了这么多年博客，尝试第一个付（打）费（赏）专栏，为小宝赚点奶粉钱，其实github和公众号都已免费开源，且作者更多的博客尤其基础性文章，一直是免费分享。该专栏也会用心撰写，望对得起读者。如果有问题随时私聊我，只望您能从这个系列中学到知识，一起加油喔~

前文赏析：

一.什么是Autoencoder

自编码器（autoencoder, AE）是一类在半监督学习和非监督学习中使用的人工神经网络（Artificial Neural Networks, ANNs），其功能是通过将输入信息作为学习目标，对输入信息进行表征学习（representation learning）。自编码器包含编码器（encoder）和解码器（decoder）两部分 。

(1) 首先，什么是自编码（Autoencoder）？
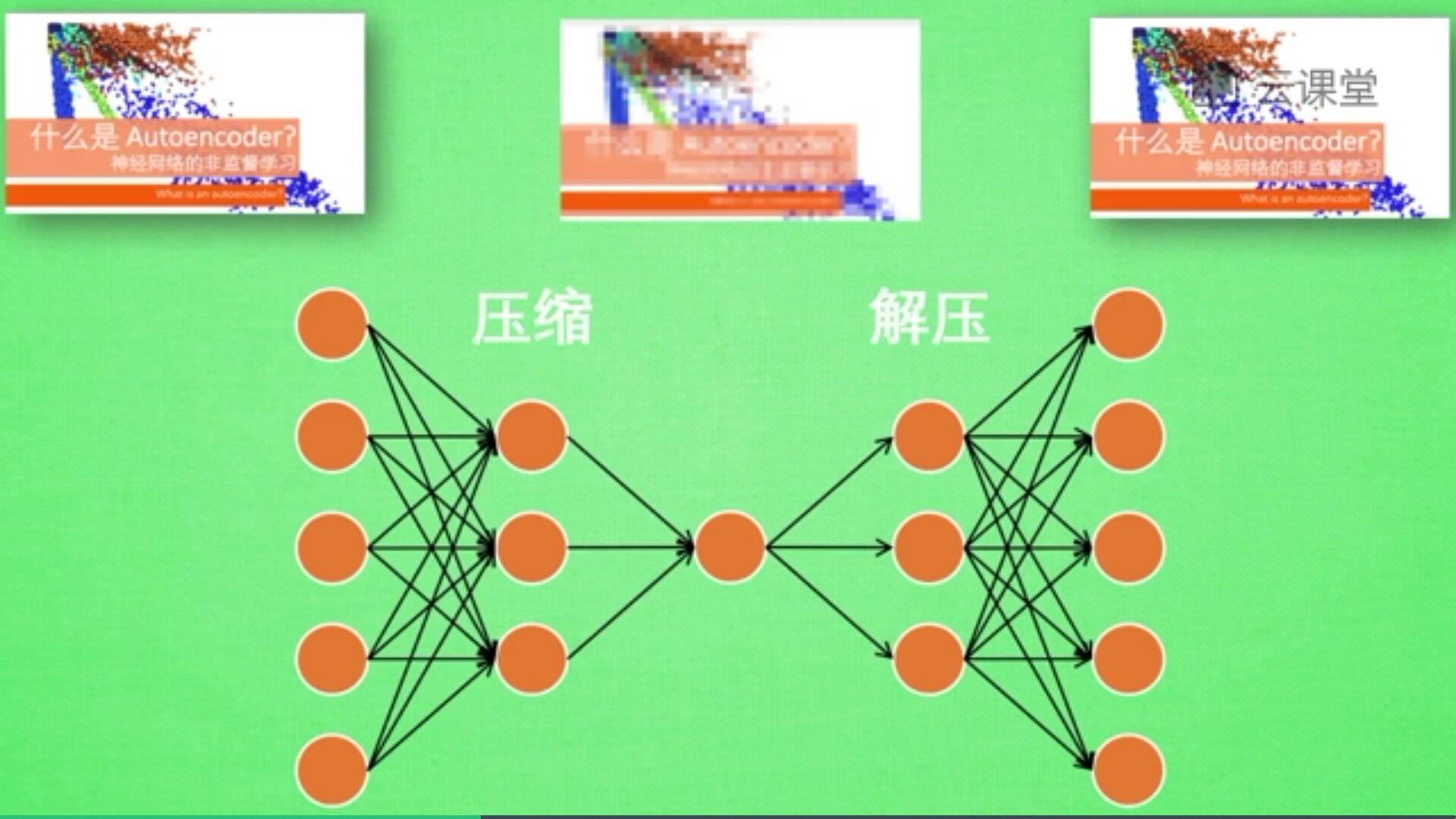
自编码是一种神经网络的形式，注意它是无监督学习算法。例如现在有一张图片，需要给它打码，然后又还原图片的过程，如下图所示：

一张图片经过压缩再解压的工序，当压缩时原有的图片质量被缩减，当解压时用信息量小却包含所有关键性文件恢复出原来的图片。为什么要这么做呢？有时神经网络需要输入大量的信息，比如分析高清图片时，输入量会上千万，神经网络从上千万中学习是非常难的一个工作，此时需要进行压缩，提取原图片中具有代表性的信息或特征，压缩输入的信息量，再把压缩的信息放入神经网络中学习。这样学习就变得轻松了，所以自编码就在这个时候发挥作用。

如下图所示，将原数据白色的X压缩解压成黑色的X，然后通过对比两个X，求出误差，再进行反向的传递，逐步提升自编码的准确性。

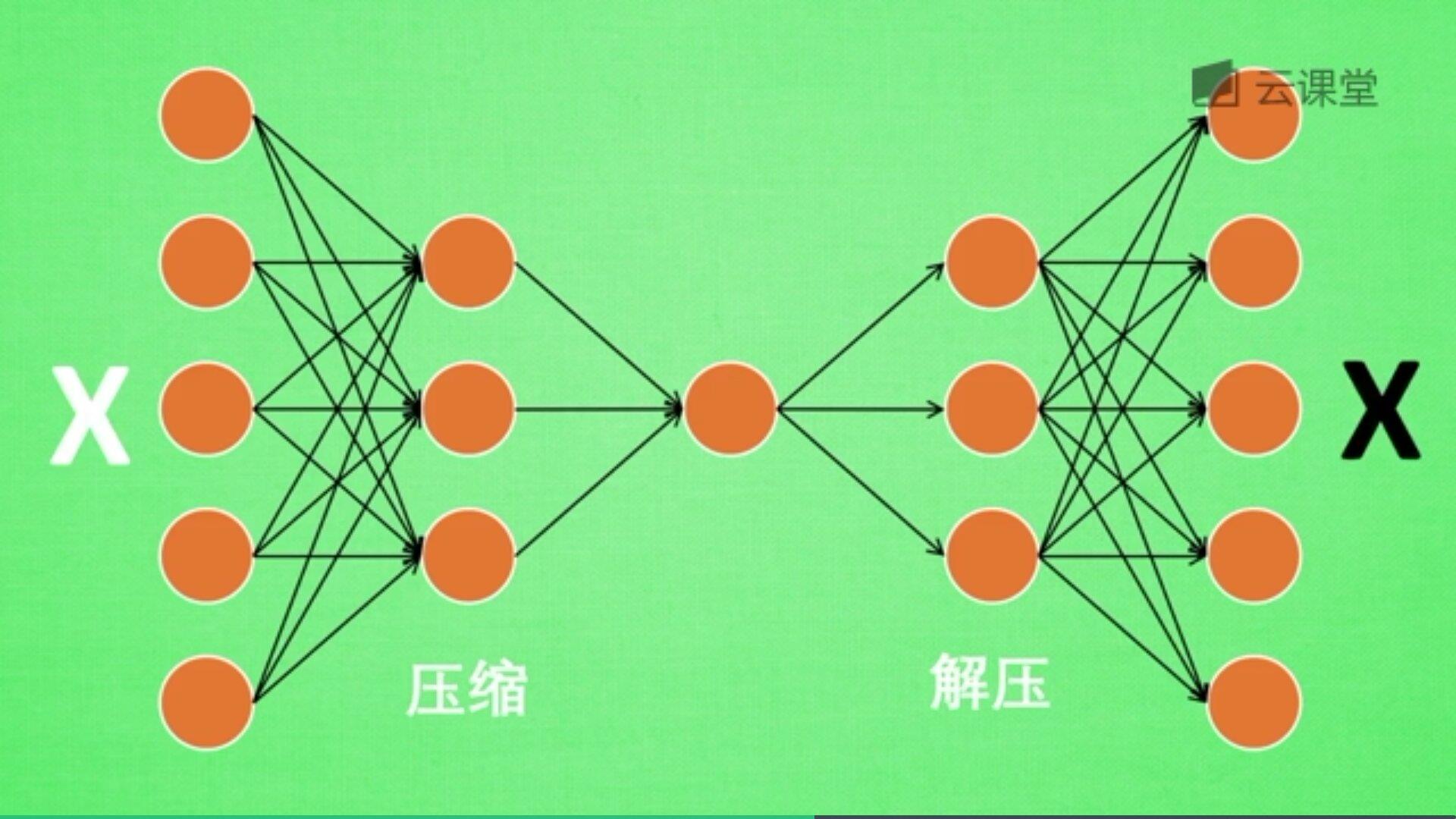
训练好的自编码，中间那部分就是原数据的精髓，从头到尾我们只用到了输入变量X，并没有用到输入变量对应的标签，所以自编码是一种无监督学习算法。

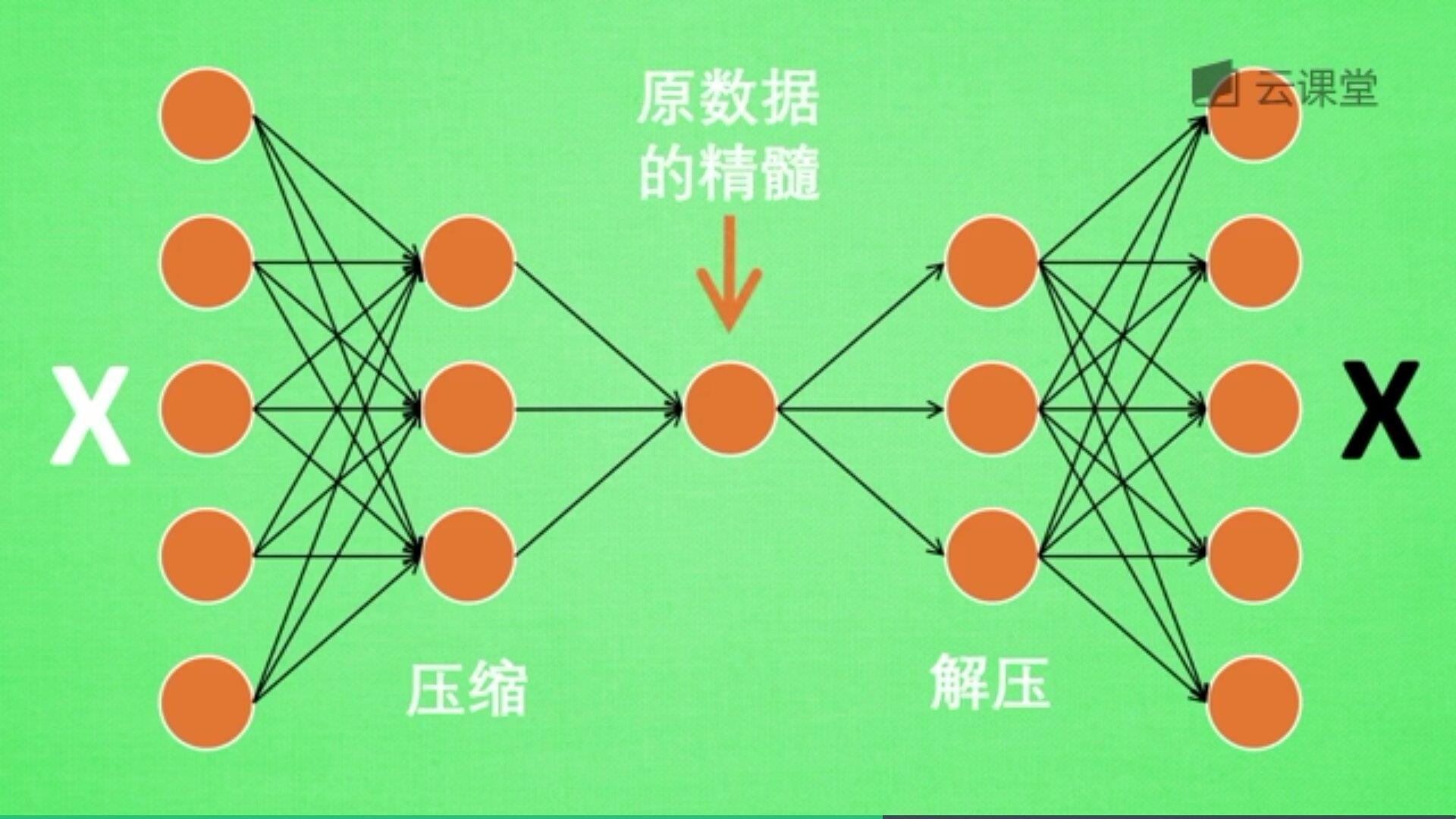
但是真正使用自编码时，通常只用到它的前半部分，叫做编码器，能得到原数据的精髓。然后只需要创建小的神经网络进行训练，不仅减小了神经网络的负担，而且同样能达到很好的效果。

(2) 自编码器的计算过程
在真实场景中，自编码器会不断计算原始数据和重构数据之间的误差，再反向传递提升自编码器的准确性，由于整个过程没有用到输入数据对应的标签，因此自编码器是一种无监督学习算法。自编码器的关键是编码器和解码器，假设给定输入空间和特征空间，自编码器求解两者的映射f和g，使得输入特征的重构误差最小，其计算过程如下：

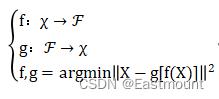
下图是自编码整理出来的数据，它能总结出每类数据的特征，如果把这些数据放在一张二维图片上，每一种数据都能很好的用其精髓把原数据区分开来。自编码能类似于PCA（主成分分析）一样提取数据特征，也能用来降维，其降维效果甚至超越了PCA。

(3) 自编码器的应用场景
自编码器具有一般意义上表征学习算法的功能，常用场景包括：

  • 降维（dimensionality reduction）
  • 异常值检测（anomaly detection）
  • 文本聚类
  • 数据去燥
  • 图像修复
  • 信道压缩与重建
  • 信息检索
  • …

自编码器在其研究早期是为解决表征学习中的“编码器问题（encoder problem）”，即基于神经网络的降维问题而提出的联结主义模型的学习算法。1985年，David H. Ackley、Geoffrey E. Hinton和Terrence J. Sejnowski在玻尔兹曼机上对自编码器算法进行了首次尝试，并通过模型权重对其表征学习能力进行了讨论 。在1986年反向传播算法（Back-Propagation, BP）被正式提出后，自编码器算法作为BP的实现之一，即“自监督的反向传播（Self-supervised BP）”得到了研究 ，并在1987年被Jeffrey L. Elman和David Zipser用于语音数据的表征学习试验。

自编码器作为一类神经网络结构（包含编码器和解码器两部分）的正式提出，来自1987年Yann LeCun发表的研究。LeCun (1987)使用多层感知器（Multi-Layer Perceptron, MLP）构建了包含编码器和解码器的神经网络，并将其用于数据降噪。此外，在同一时期，Bourlard and Kamp (1988)使用MLP自编码器对数据降维进行的研究也得到了关注。1994年，Hinton和Richard S. Zemel通过提出“最小描述长度原理（Minimum Description Length principle, MDL）”构建了第一个基于自编码器的生成模型 。
——百度百科 https://baike.baidu.com/item/自编码器/23686966

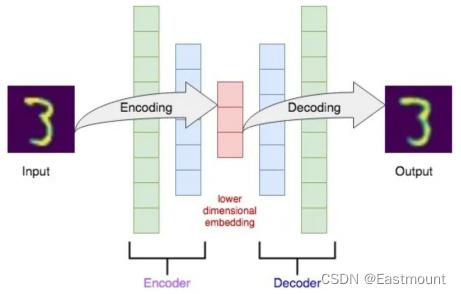
二.Autoencoder分析MNIST数据

Autoencoder算法属于非监督学习，它是把数据特征压缩，再把压缩后的特征解压的过程，跟PCA降维压缩类似。本篇文章的代码包括两部分内容：

  • 第一部分：使用MNIST数据集，通过feature的压缩和解压，对比解压后的图片和压缩之前的图片，看看是否一致，实验想要的效果是和图片压缩之前的差不多。
  • 第二部分：输出encoder的结果，压缩至两个元素并可视化显示。在显示图片中，相同颜色表示同一类型图片，比如类型为1（数字1），类型为2（数字2）等等，最终实现无监督的聚类。

有监督学习和无监督学习的区别：
(1) 有监督学习方法必须要有训练集与测试样本。在训练集中找规律，而对测试样本使用这种规律。而非监督学习没有训练集，只有一组数据，在该组数据集内寻找规律。
(2) 有监督学习的方法就是识别事物，识别的结果表现在给待识别数据加上了标签。因此训练样本集必须由带标签的样本组成。而非监督学习方法只有要分析的数据集的本身，预先没有什么标签。 如果发现数据集呈现某种聚集性，则可按自然的聚集性分类，但不予以某种预先分类标签对上号为目的。

让我们开始编写代码吧！采用Keras构建。


第一步，打开Anaconda，然后选择已经搭建好的“tensorflow”环境，运行Spyder。


第二步，导入扩展包。

import numpy as np
from keras.datasets import mnist
from keras.utils import np_utils
from keras.models import Model
from keras.layers import Dense, Input
import matplotlib.pyplot as plt

第三步，下载数据集。
由于MNIST数据集是TensorFlow的示例数据，所以我们只需要下面一行代码，即可实现数据集的读取工作。如果数据集不存在它会在线下载，如果数据集已经被下载，它会被直接调用。

  • 注意，仅使用x数据集
#-------------------------下载MNIST数据--------------------------------
(x_train, _), (x_test, y_test) = mnist.load_data()
print(x_train.shape, x_test.shape, _.shape, y_test.shape)

输出结果如下，MNIST图片是28*28的像素，包括6万张训练集和1万张测试集。

(60000, 28, 28) (10000, 28, 28) (60000,) (10000,)

第四步，数据预处理。
通过minmax_normalized处理至(-0.5,0.5)区间，再修改其形状。

#---------------------------数据预处理--------------------------------
x_train = x_train.astype('float32') / 255. - 0.5 
x_test = x_test.astype('float32') / 255. - 0.5
x_train = x_train.reshape((x_train.shape[0], -1))
x_test = x_test.reshape((x_test.shape[0], -1))
print(x_train.shape, x_test.shape)

输出如下：

(60000, 784) (10000, 784)

第五步，编写核心代码，即定义encoder和decoder函数来实现压缩和解压操作。
整个自编码器的输入特征为784，feature不断压缩，先压缩成128个，再经过一层隐藏层压缩到64个，再压缩至10，最终压缩成两维特征（方便可视化聚类）。然后把2个特征依次放大，最终解压成784个。最后对解压的784个和原始的784个特征进行cost对比，并根据cost提升Autoencoder的准确率。

#-----------------------构建Encoder和Decoder层-----------------------
#降维可视化绘制2D图
encoding_dim = 2

#input placeholder 28*28
input_img = Input(shape=(784,))

#Encoder layers（压缩）
encoded = Dense(128, activation='relu')(input_img)
encoded = Dense(64, activation='relu')(encoded)
encoded = Dense(10, activation='relu')(encoded)
encoder_output = Dense(encoding_dim,)(encoded)

#Decoder Layers（解压）
decoded = Dense(10, activation='relu')(encoder_output)
decoded = Dense(64, activation='relu')(decoded)
decoded = Dense(128, activation='relu')(decoded)
decoded = Dense(784, activation='tanh')(decoded)

关键代码解析如下，encoder和decoder均包括四层，具体含义为：

  • encoded = Dense(128, activation=‘relu’)(input_img)
    利用Dense构造Encoder层，其输出值为128，输入值为input_img
  • encoded = Dense(64, activation=‘relu’)(encoded)
    第二层的输出是64，输入是上一个构建的encoded
  • encoded = Dense(10, activation=‘relu’)(encoded)
    第三层压缩至10
  • encoder_output = Dense(encoding_dim,)(encoded)
    最后构建需要的自编码压缩器，压缩成2个值，它能代表整个784个特征，并且可用于聚类

通常Encoder怎么构建，Decoder也对应反向构建，实现解压处理，重构至784个特征，关键代码如下：

  • decoded = Dense(10, activation=‘relu’)(encoder_output)
  • decoded = Dense(64, activation=‘relu’)(decoded)
  • decoded = Dense(128, activation=‘relu’)(decoded)
  • decoded = Dense(784, activation=‘tanh’)(decoded)
    由于输入值是(-0.5,0.5)，而使用tanh激活函数的范围是(-1,1)，因此实现对应效果

第六步，构造自编码器模型，同时构建encoder模型进行可视化分析。

#构造自编码器模型
autoencoder = Model(inputs=input_img, outputs=decoded)

#构建encoder模型进行可视化分析
encoder = Model(inputs=input_img, outputs=encoder_output)

#激活自编码器
autoencoder.compile(optimizer='adam', loss='mse')

第七步，训练、测试和可视化代码，该部分为神经网络运行的核心代码。
输入和输出均是x_train，对比二者形成误差。可视化包括：

  • 调用matplotlib库画图，可视化对比原始图像和预测图像
  • 压缩结果聚类分析
#-----------------------------训练和测试------------------------------
#训练
autoencoder.fit(x_train, 
                x_train, 
                epochs=20,
                batch_size=256,
                shuffle=True)

#预测
encoded_imgs = encoder.predict(x_test)     #压缩二维特征 用于聚类
decoded_imgs = autoencoder.predict(x_test) #自编码器还原的图像

#比较原始图像和预测图像数据
f, a = plt.subplots(2, 10, figsize=(10, 2))
for i in range(10):
    a[0][i].imshow(np.reshape(x_test[i], (28, 28)))
    a[1][i].imshow(np.reshape(decoded_imgs[i], (28, 28)))
plt.show()

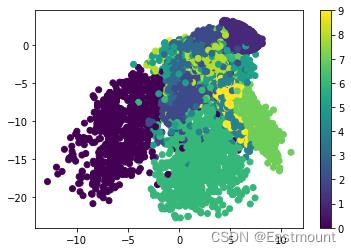
#聚类分析
plt.scatter(encoded_imgs[:,0], encoded_imgs[:,1], c=y_test)
plt.colorbar()
plt.show()

运行结果如下所示：

(60000, 28, 28) (10000, 28, 28) (60000,) (10000,)
(60000, 784) (10000, 784)
Epoch 1/20
235/235 [==============================] - 2s 5ms/step - loss: 0.0697
Epoch 2/20
235/235 [==============================] - 1s 6ms/step - loss: 0.0564
Epoch 3/20
235/235 [==============================] - 1s 5ms/step - loss: 0.0516
Epoch 4/20
235/235 [==============================] - 1s 6ms/step - loss: 0.0493
Epoch 5/20
235/235 [==============================] - 1s 6ms/step - loss: 0.0475
Epoch 6/20
235/235 [==============================] - 1s 5ms/step - loss: 0.0462
Epoch 7/20
235/235 [==============================] - 1s 6ms/step - loss: 0.0453
Epoch 8/20
235/235 [==============================] - 1s 5ms/step - loss: 0.0446
Epoch 9/20
235/235 [==============================] - 1s 5ms/step - loss: 0.0439
Epoch 10/20
235/235 [==============================] - 2s 6ms/step - loss: 0.0432
Epoch 11/20
235/235 [==============================] - 2s 7ms/step - loss: 0.0427
Epoch 12/20
235/235 [==============================] - 2s 7ms/step - loss: 0.0421
Epoch 13/20
235/235 [==============================] - 2s 7ms/step - loss: 0.0418
Epoch 14/20
235/235 [==============================] - 2s 7ms/step - loss: 0.0414
Epoch 15/20
235/235 [==============================] - 2s 8ms/step - loss: 0.0411
Epoch 16/20
235/235 [==============================] - 2s 8ms/step - loss: 0.0409
Epoch 17/20
235/235 [==============================] - 2s 6ms/step - loss: 0.0406
Epoch 18/20
235/235 [==============================] - 2s 7ms/step - loss: 0.0404
Epoch 19/20
235/235 [==============================] - 2s 7ms/step - loss: 0.0401
Epoch 20/20
235/235 [==============================] - 2s 7ms/step - loss: 0.0400

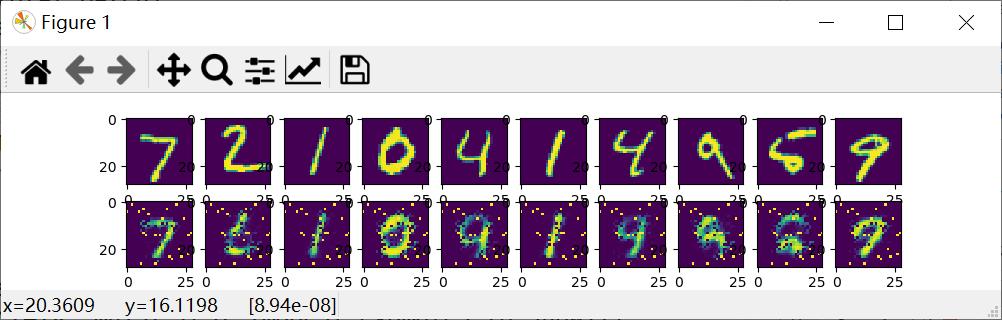
通过20批训练，显示结果如下图所示，上面是真实的原始图像，下面是压缩之后再解压的图像数据。

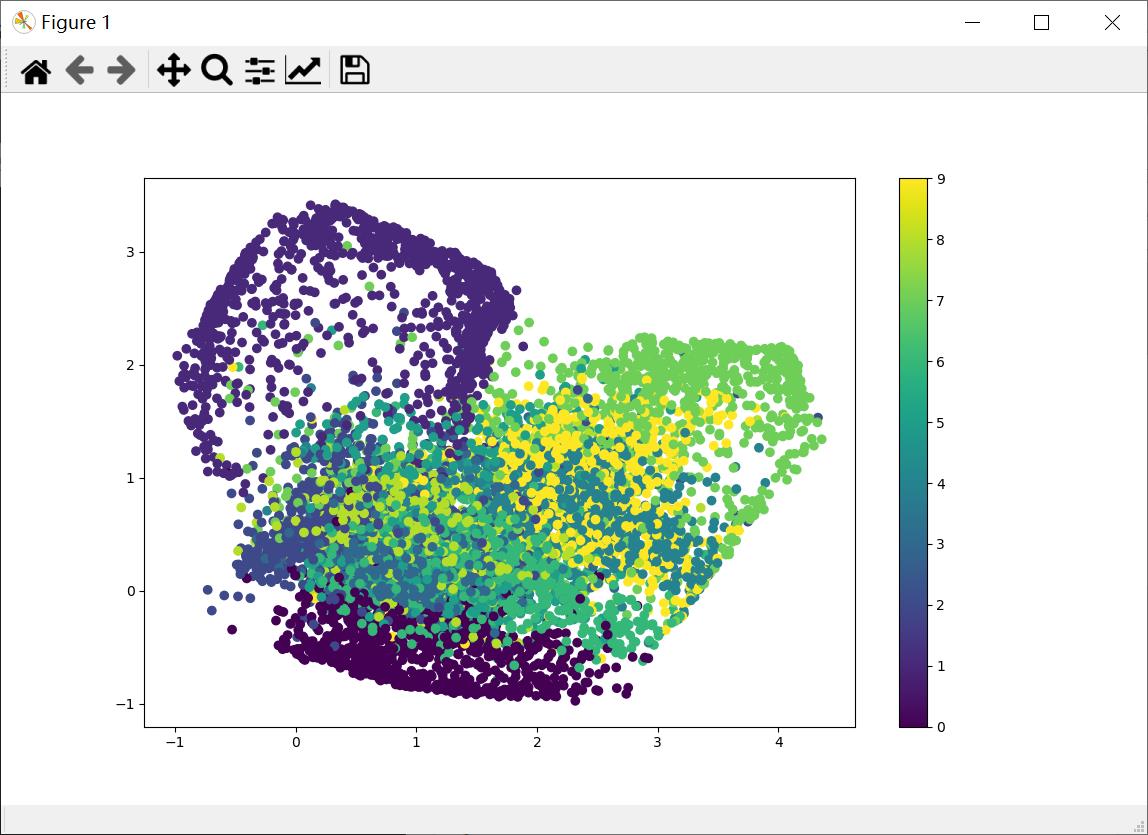
聚类显示结果如下图所示，它将不同颜色的分在一堆，对应不同的数字。

三.完整代码

最后给出完整代码，也希望读者能将自编码器应用到更多场景中。同时，整个聚类结果还有待改善，因为这只是Autoencoder的一个简单例子。希望这篇文章能够帮助博友们理解和认识无监督学习和Autoencoder算法，后续作者会更深入的分享好案例。

# -*- coding: utf-8 -*-
# By：Eastmount CSDN 2022-08-23
import numpy as np
from keras.datasets import mnist
from keras.utils import np_utils
from keras.models import Model
from keras.layers import Dense, Input
import matplotlib.pyplot as plt

#-------------------------下载MNIST数据--------------------------------
#只使用x数据集
(x_train, _), (x_test, y_test) = mnist.load_data()
print(x_train.shape, x_test.shape, _.shape, y_test.shape)以上是关于[Python人工智能] 三十八.Keras构建无监督学习Autoencoder模型及MNIST聚类可视化详解的主要内容，如果未能解决你的问题，请参考以下文章
 

 [Python人工智能] 三十九.VS Code配置Python编程和Keras环境及手写数字识别（基础篇）


 [Python人工智能] 三十九.VS Code配置Python编程和Keras环境及手写数字识别（基础篇）


 [Python人工智能] 三十.Keras深度学习构建CNN识别阿拉伯手写文字图像


 [Python人工智能] 三十六.基于Transformer的商品评论情感分析 keras构建多头自注意力（Transformer）模型


 [Python人工智能] 三十六.基于Transformer的商品评论情感分析 keras构建多头自注意力（Transformer）模型


 [Python人工智能] 三十三.Bert模型 keras-bert库构建Bert模型实现文本分类