浮点数表示法（总结自CS61C和CMU CSAPP）

Posted 2022-11-23 只是有点小怂

• 总结自伯克利的CS61C2021秋季课程，Nick主讲和CMU2015年讲CS APP的课程，标题均是floating point，相比而言CMU讲得比较详细，我先看了一遍CS61C再看了一遍CMU的课程，点击floating point点击slides可以下载pdf（讲得很详细可以自己看一下，我挑了几张贴出来），课程主页https://inst.eecs.berkeley.edu/~cs61c/fa21/
  

• P&H是课本章节，中文版是计算机组成与设计硬件软件接口RISCV
  

• 还有个浮点数网站可以玩一玩https://www.h-schmidt.net/FloatConverter/IEEE754.html
  

• 浮点数表示法是伯克利提出的，因为小数点是可以浮动的，降低了精度但是表示范围变大了(Can represent a very large range with roughly the same “precision”)，而且希望和整数的补码表示法一致（32个0还是0），并且希望不用对浮点数进行比较就能排序(Make it possible to sort without needing to do floating-point comparisons)

• float是单精度32位4字节，double是8字节双精度，先掌握float，float不能表示的就有+∞, -∞, Not-A-Number (NaN), exponent overflow, exponent underflow, +/- zero这么多种特殊情况，能表示的又分为normal format和denorm，最大可表示到$2^{127}=2^{120}\ast 2^7=128\ast (2^{10}{)}^{12}=128\ast 10^{36}=2\ast 10^{38}$，根据$2^{10}=10^3$换算得到
  

• 偏置计算方法bias = 2 ^ (k - 1) - 1，k 是指数位数，8位指数计算得到bias = 127（正数负数各站一半，bias gives us a balanced value），小数部分可以表示为fraction, F, mantissa, M, significand
  

• 先掌握normal format，即1.xxx
  

• denorm format用于表示0附近的数，0.xxx，指数部分为0000_0000，此时小数部分不需要+1，然后指数部分E = 1 - Bias（这一部分CMU讲得比较好，为了实现两种表示方法的平滑过渡，可以用8位数字，指数部分k = 4偏置为7，小数部分为3位），老师当时评论those IEEE folks are really smart
  

• overflow部分指数部分为1111_1111，首先是Inf然后是NaN，NAN通常是sqer(-1)或者0/0，NAN不能比较大小，+INF是1.0/0.0，-INF是-1.0/0.0，INF可以比较大小
  

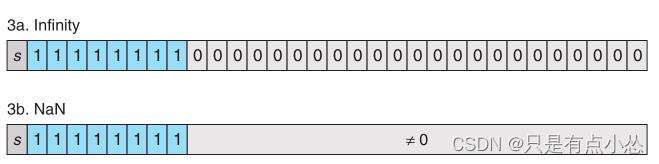
• 浮点数中存在+/- 0，表示太小而不能表示的数字
  

• 总结一下
  

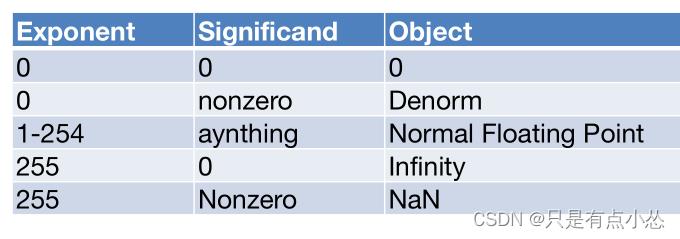
• 如何比较浮点数，先比较符号位再比较指数（无符号比较，使用偏置可以直接比较大小，如果使用补码不能直接比较大小），最后比较小数部分（指数部分比较重要用于区分数字分布，在数轴上可以看出）
  

• CMU课程中得C代码可以写一下，看下是如何得到NAN和INF的，直接定义a = 1e20，CMU课程中老师讲得好，这些0和1其实不是真实的数字，只是我们看待问题的角度不同（大意）