怎么比较两个向量组相似度

Posted 2023-04-11

我们都知道比较向量相似度可以用余弦夹角来判断
那么问题是如果我有两个向量组，这两个向量组向量都是相似的，但是排列是随机的，
有没得简便算法得到相似度？
比如向量组1包含 [1 0 0] [1 1 1] [3 4 5] 而向量组2包含[1.1 0.9 1.0] [3.2 3.8 5.3] [1.1 0 0.1] 如何用矩阵的方法得到一个相似度呢

相关性是数据属性相关性的度量方法，相似度是数据对象相似性度量的方法，数据对象由多个数据属性描述，数据属性的相关性由相关系数来描述，数据对象的相似性由某种距离度量。许多数据分析算法会涉及相似性度量和相关性度量，如聚类、KNN等。

相关性度量

相关性用相关系数来度量，相关系数种类如下图所示。相关系数绝对值越大表是相关性越大，相关系数取值在-1–1之间，0表示不相关。各系数计算表达式和取值范围参考 相关性与相似性度量
这里写图片描述

相似性度量

相似度用距离来度量，相似度度量指标种类如下图所示。相似度通常是非负的，取值在0-1之间。距离越大，相似性越小，在应用过程中要注意计算的是相似度还是距离。
这里写图片描述
Jaccard（杰卡德相似系数）
两个集合A和B的交集元素在A，B的并集中所占的比例 这里写图片描述
杰卡德距离用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度这里写图片描述
Cosine（余弦相似度）
在二维空间中向量A(x1,y1)与向量B(x2,y2)的夹角余弦公式这里写图片描述
夹角余弦取值范围为[-1,1]。当两个向量的方向重合时夹角余弦取最大值1，当两个向量的方向完全相反夹角余弦取最小值-1，两个方向正交时夹角余弦取值为0.

Minkowski Distance（闵可夫斯基距离）
两个n维变量间的闵可夫斯基距离定义为：这里写图片描述
当p=1时，就是曼哈顿距离，两点间各边距离之和
当p=2时，就是欧氏距离，两点间直线距离
当p→∞时，就是切比雪夫距离，所有边距离的最大值
闵氏距离的缺点(1)数据量纲不同，无法直接进行距离计算，需要先对数据进行归一化(2)没有考虑各个分量的分布（期望，方差等)。下图展示了不同距离函数是怎么逼近中心的在这里插入图片描述

Mahalanobis Distance（马氏距离）
马氏距离计算公式为这里写图片描述
S为协方差矩阵， 若协方差矩阵是单位矩阵则变为欧式距离。马氏距离的优点是量纲无关、排除变量之间的相关性的干扰。

Hamming distance(汉明距离)
两个等长字符串s1与s2之间的汉明距离定义为将其中一个变为另外一个所需要作的最小替换次数。例如字符串“1111”与“1010”之间的汉明距离为2。信息编码时为了增强容错性，应使得编码间的最小汉明距离尽可能大。

K-L散度（相对熵）
是衡量两个分布(P、Q)之间的距离；越小越相似这里写图片描述
Hellinger距离
在概率论和统计理论中，Hellinger距离被用来度量两个概率分布的相似度。它是f散度的一种（f散度——度量两个概率分布相似度的指标）。
概率密度函数分别表示为 f 和 g，两个概率密度函数的Hellinger距离的平方为
在这里插入图片描述

具有混合类型属性的对象可以将相同类型的属性划分为一组，对每组属性分析继续相似度度量，也可以分别对每个属性进行相似度度量再加权。

其他类型的距离度量可以参考 18种和“距离(distance)”、“相似度(similarity)”相关的量的小结 参考技术A 其次,要正确看待自己嘴笨不会说话这件事情。自己之所以嘴笨不会说话,并不是说明自己比别人差,因为每个人都有自己擅长的一面,不要因为嘴笨不会说话就全面的否定自己。嘴笨不会说话往往是成长环境造成的,小时候的我们无法选择自己的成长环境,但是长大了成年了的时候,我们要对自己负责。20岁以前,我们被父母被成长环境决定,但30岁以后自己是什么样子的人是由自己决定的。所以,20几岁的你,应该从此刻开始,积极的改变自己。那可能是她把你看作家里人了！因为清明节是要给家里已过世的至亲祭拜的！没把你当外人，当自己人了！她这么表达虽然有点含蓄，但寓意很明显!你真是直男癌!愿意就留下一起过清明节，不愿意就找理由婉拒别人一片好意!加油1111111111111111111111111111其次,要正确看待自己嘴笨不会说话这件事情。自己之所以嘴笨不会说话,并不是说明自己比别人差,因为每个人都有自己擅长的一面,不要因为嘴笨不会说话就全面的否定自己。嘴笨不会说话往往是成长环境造成的,小时候的我们无法选择自己的成长环境,但是长大了成年了的时候,我们要对自己负责。20岁以前,我们被父母被成长环境决定,但30岁以后自己是什么样子的人是由自己决定的。所以,20几岁的你,应该从此刻开始,积极的改变自己。那可能是她把你看作家里人了！因为清明节是要给家里已过世的至亲祭拜的！没把你当外人，当自己人了！她这么表达虽然有点含蓄，但寓意很明显!你真是直男癌!愿意就留下一起过清明节，不愿意就找理由婉拒别人一片好意!加油1111111111111111111111111111突击 参考技术B 全文百度云 参考技术C 作品鉴赏编辑

智能推荐算法基础-余弦相似度计算

余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。余弦值越接近1，就表明夹角越接近0度，也就是两个向量越相似，这就叫"余弦相似性"。

我们知道，对于两个向量，如果他们之间的夹角越小，那么我们认为这两个向量是越相似的。余弦相似性就是利用了这个理论思想。它通过计算两个向量的夹角的余弦值来衡量向量之间的相似度值。余弦相似性推导公式如下：

 

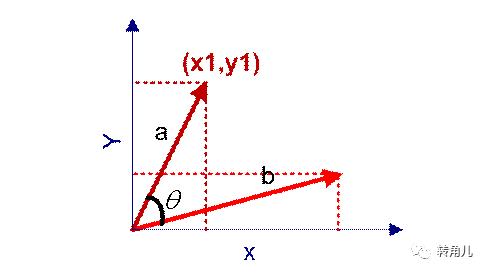
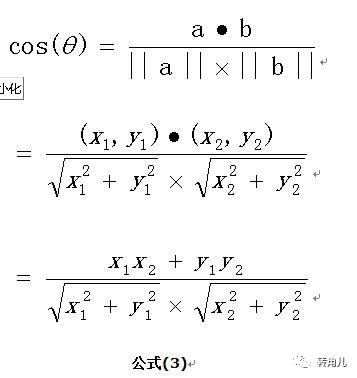
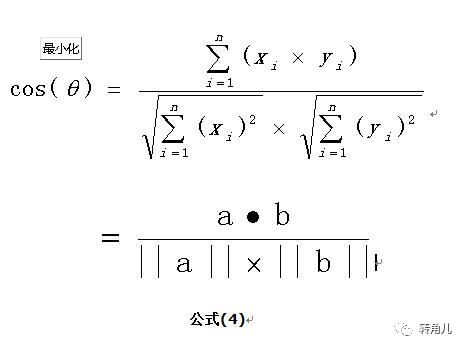
【下面举一个例子，来说明余弦计算文本相似度】

    举一个例子来说明，用上述理论计算文本的相似性。为了简单起见，先从句子着手。

       句子A：这只皮靴号码大了。那只号码合适

句子B：这只皮靴号码不小，那只更合适

怎样计算上面两句话的相似程度？

基本思路是：如果这两句话的用词越相似，它们的内容就应该越相似。因此，可以从词频入手，计算它们的相似程度。

第一步，分词。

句子A：这只/皮靴/号码/大了。那只/号码/合适。

句子B：这只/皮靴/号码/不/小，那只/更/合适。

第二步，列出所有的词。

这只，皮靴，号码，大了。那只，合适，不，小，很

第三步，计算词频。

句子A：这只1，皮靴1，号码2，大了1。那只1，合适1，不0，小0，更0

句子B：这只1，皮靴1，号码1，大了0。那只1，合适1，不1，小1，更1

第四步，写出词频向量。

句子A：(1，1，2，1，1，1，0，0，0)

　　句子B：(1，1，1，0，1，1，1，1，1)

到这里，问题就变成了如何计算这两个向量的相似程度。我们可以把它们想象成空间中的两条线段，都是从原点（[0, 0, ...]）出发，指向不同的方向。两条线段之间形成一个夹角，如果夹角为0度，意味着方向相同、线段重合,这是表示两个向量代表的文本完全相等；如果夹角为90度，意味着形成直角，方向完全不相似；如果夹角为180度，意味着方向正好相反。因此，我们可以通过夹角的大小，来判断向量的相似程度。夹角越小，就代表越相似。

使用上面的公式(4)

 

计算两个句子向量

句子A：(1，1，2，1，1，1，0，0，0)

和句子B：(1，1，1，0，1，1，1，1，1)的向量余弦值来确定两个句子的相似度。

计算过程如下：

 

计算结果中夹角的余弦值为0.81非常接近于1，所以，上面的句子A和句子B是基本相似的