BP神经网络预测(python)
Posted 积极向上的mr.d
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了BP神经网络预测(python)相关的知识,希望对你有一定的参考价值。
可以参考新发布的文章
1.mlp多层感知机预测(python)
2.lstm时间序列预测+GRU(python)
下边是基于Python的简单的BP神经网络预测,多输入单输出,也可以改成多输入多输出,下边是我的数据,蓝色部分预测红色(x,y,v为自变量,z为因变量)
数据集下载链接1,点击下载
数据集下载链接2(github),点击下载

话不多说,直接上代码
# -*- coding: utf-8 -*-
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import BPNN
from sklearn import metrics
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
#导入必要的库
df1=pd.read_excel('2000.xls',0)
df1=df1.iloc[:,:]
#进行数据归一化
from sklearn import preprocessing
min_max_scaler = preprocessing.MinMaxScaler()
df0=min_max_scaler.fit_transform(df1)
df = pd.DataFrame(df0, columns=df1.columns)
x=df.iloc[:,:-1]
y=df.iloc[:,-1]
#划分训练集测试集
cut=300#取最后cut=30天为测试集
x_train, x_test=x.iloc[:-cut],x.iloc[-cut:]#列表的切片操作,X.iloc[0:2400,0:7]即为1-2400行,1-7列
y_train, y_test=y.iloc[:-cut],y.iloc[-cut:]
x_train, x_test=x_train.values, x_test.values
y_train, y_test=y_train.values, y_test.values
#神经网络搭建
bp1 = BPNN.BPNNRegression([3, 16, 1])
train_data = [[sx.reshape(3,1), sy.reshape(1,1)] for sx, sy in zip(x_train, y_train)]
test_data = [np.reshape(sx, (3,1)) for sx in x_test]
#神经网络训练
bp1.MSGD(train_data, 60000, len(train_data), 0.2)
#神经网络预测
y_predict=bp1.predict(test_data)
y_pre = np.array(y_predict) # 列表转数组
y_pre=y_pre.reshape(300,1)
y_pre=y_pre[:,0]
#画图 #展示在测试集上的表现
draw=pd.concat([pd.DataFrame(y_test),pd.DataFrame(y_pre)],axis=1);
draw.iloc[:,0].plot(figsize=(12,6))
draw.iloc[:,1].plot(figsize=(12,6))
plt.legend(('real', 'predict'),loc='upper right',fontsize='15')
plt.title("Test Data",fontsize='30') #添加标题
#输出精度指标
print('测试集上的MAE/MSE')
print(mean_absolute_error(y_pre, y_test))
print(mean_squared_error(y_pre, y_test) )
mape = np.mean(np.abs((y_pre-y_test)/(y_test)))*100
print('=============mape==============')
print(mape,'%')
# 画出真实数据和预测数据的对比曲线图
print("R2 = ",metrics.r2_score(y_test, y_pre)) # R2
下边是神经网络内部结构,文件名命名为 BPNN.py
# encoding:utf-8
'''
BP神经网络Python实现
'''
import random
import numpy as np
def sigmoid(x):
'''
激活函数
'''
return 1.0 / (1.0 + np.exp(-x))
def sigmoid_prime(x):
return sigmoid(x) * (1 - sigmoid(x))
class BPNNRegression:
'''
神经网络回归与分类的差别在于:
1. 输出层不需要再经过激活函数
2. 输出层的 w 和 b 更新量计算相应更改
'''
def __init__(self, sizes):
# 神经网络结构
self.num_layers = len(sizes)
self.sizes = sizes
# 初始化偏差,除输入层外, 其它每层每个节点都生成一个 biase 值(0-1)
self.biases = [np.random.randn(n, 1) for n in sizes[1:]]
# 随机生成每条神经元连接的 weight 值(0-1)
self.weights = [np.random.randn(r, c)
for c, r in zip(sizes[:-1], sizes[1:])]
def feed_forward(self, a):
'''
前向传输计算输出神经元的值
'''
for i, b, w in zip(range(len(self.biases)), self.biases, self.weights):
# 输出神经元不需要经过激励函数
if i == len(self.biases) - 1:
a = np.dot(w, a) + b
break
a = sigmoid(np.dot(w, a) + b)
return a
def MSGD(self, training_data, epochs, mini_batch_size, eta, error = 0.01):
'''
小批量随机梯度下降法
'''
n = len(training_data)
for j in range(epochs):
# 随机打乱训练集顺序
random.shuffle(training_data)
# 根据小样本大小划分子训练集集合
mini_batchs = [training_data[k:k+mini_batch_size]
for k in range(0, n, mini_batch_size)]
# 利用每一个小样本训练集更新 w 和 b
for mini_batch in mini_batchs:
self.updata_WB_by_mini_batch(mini_batch, eta)
#迭代一次后结果
err_epoch = self.evaluate(training_data)
print("Epoch 0 Error 1".format(j, err_epoch))
if err_epoch < error:
break
# if test_data:
# print("Epoch 0: 1 / 2".format(j, self.evaluate(test_data), n_test))
# else:
# print("Epoch 0".format(j))
return err_epoch
def updata_WB_by_mini_batch(self, mini_batch, eta):
'''
利用小样本训练集更新 w 和 b
mini_batch: 小样本训练集
eta: 学习率
'''
# 创建存储迭代小样本得到的 b 和 w 偏导数空矩阵,大小与 biases 和 weights 一致,初始值为 0
batch_par_b = [np.zeros(b.shape) for b in self.biases]
batch_par_w = [np.zeros(w.shape) for w in self.weights]
for x, y in mini_batch:
# 根据小样本中每个样本的输入 x, 输出 y, 计算 w 和 b 的偏导
delta_b, delta_w = self.back_propagation(x, y)
# 累加偏导 delta_b, delta_w
batch_par_b = [bb + dbb for bb, dbb in zip(batch_par_b, delta_b)]
batch_par_w = [bw + dbw for bw, dbw in zip(batch_par_w, delta_w)]
# 根据累加的偏导值 delta_b, delta_w 更新 b, w
# 由于用了小样本,因此 eta 需除以小样本长度
self.weights = [w - (eta / len(mini_batch)) * dw
for w, dw in zip(self.weights, batch_par_w)]
self.biases = [b - (eta / len(mini_batch)) * db
for b, db in zip(self.biases, batch_par_b)]
def back_propagation(self, x, y):
'''
利用误差后向传播算法对每个样本求解其 w 和 b 的更新量
x: 输入神经元,行向量
y: 输出神经元,行向量
'''
delta_b = [np.zeros(b.shape) for b in self.biases]
delta_w = [np.zeros(w.shape) for w in self.weights]
# 前向传播,求得输出神经元的值
a = x # 神经元输出值
# 存储每个神经元输出
activations = [x]
# 存储经过 sigmoid 函数计算的神经元的输入值,输入神经元除外
zs = []
for b, w in zip(self.biases, self.weights):
z = np.dot(w, a) + b
zs.append(z)
a = sigmoid(z) # 输出神经元
activations.append(a)
#-------------
activations[-1] = zs[-1] # 更改神经元输出结果
#-------------
# 求解输出层δ
# 与分类问题不同,Delta计算不需要乘以神经元输入的倒数
#delta = self.cost_function(activations[-1], y) * sigmoid_prime(zs[-1])
delta = self.cost_function(activations[-1], y) #更改后
#-------------
delta_b[-1] = delta
delta_w[-1] = np.dot(delta, activations[-2].T)
for lev in range(2, self.num_layers):
# 从倒数第1层开始更新,因此需要采用-lev
# 利用 lev + 1 层的 δ 计算 l 层的 δ
z = zs[-lev]
zp = sigmoid_prime(z)
delta = np.dot(self.weights[-lev+1].T, delta) * zp
delta_b[-lev] = delta
delta_w[-lev] = np.dot(delta, activations[-lev-1].T)
return (delta_b, delta_w)
def evaluate(self, train_data):
test_result = [[self.feed_forward(x), y]
for x, y in train_data]
return np.sum([0.5 * (x - y) ** 2 for (x, y) in test_result])
def predict(self, test_input):
test_result = [self.feed_forward(x)
for x in test_input]
return test_result
def cost_function(self, output_a, y):
'''
损失函数
'''
return (output_a - y)
pass
下边是我训练10000次得出的结果图
Mape=3.8747546777023055 %
R2 = 0.9892761559285088
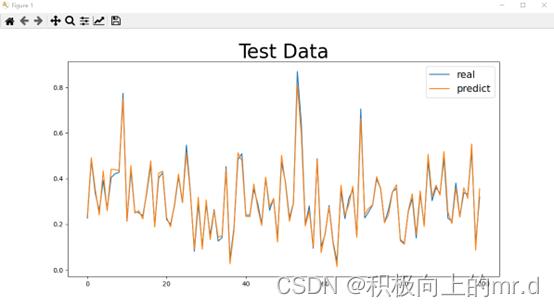
可以加群:1029655667,进行沟通交流
BP预测基于海鸥算法改进BP神经网络实现数据预测
一、 BP神经网络预测算法简介
说明:1.1节主要是概括和帮助理解考虑影响因素的BP神经网络算法原理,即常规的BP模型训练原理讲解(可根据自身掌握的知识是否跳过)。1.2节开始讲基于历史值影响的BP神经网络预测模型。
使用BP神经网络进行预测时,从考虑的输入指标角度,主要有两类模型:
1.1 受相关指标影响的BP神经网络算法原理
如图一所示,使用MATLAB的newff函数训练BP时,可以看到大部分情况是三层的神经网络(即输入层,隐含层,输出层)。这里帮助理解下神经网络原理:
1)输入层:相当于人的五官,五官获取外部信息,对应神经网络模型input端口接收输入数据的过程。
2)隐含层:对应人的大脑,大脑对五官传递来的数据进行分析和思考,神经网络的隐含层hidden Layer对输入层传来的数据x进行映射,简单理解为一个公式hiddenLayer_output=F(w*x+b)。其中,w、b叫做权重、阈值参数,F()为映射规则,也叫激活函数,hiddenLayer_output是隐含层对于传来的数据映射的输出值。换句话说,隐含层对于输入的影响因素数据x进行了映射,产生了映射值。
3)输出层:可以对应为人的四肢,大脑对五官传来的信息经过思考(隐含层映射)之后,再控制四肢执行动作(向外部作出响应)。类似地,BP神经网络的输出层对hiddenLayer_output再次进行映射,outputLayer_output=w *hiddenLayer_output+b。其中,w、b为权重、阈值参数,outputLayer_output是神经网络输出层的输出值(也叫仿真值、预测值)(理解为,人脑对外的执行动作,比如婴儿拍打桌子)。
4)梯度下降算法:通过计算outputLayer_output和神经网络模型传入的y值之间的偏差,使用算法来相应调整权重和阈值等参数。这个过程,可以理解为婴儿拍打桌子,打偏了,根据偏离的距离远近,来调整身体使得再次挥动的胳膊不断靠近桌子,最终打中。
再举个例子来加深理解:
图一所示BP神经网络,具备输入层、隐含层和输出层。BP是如何通过这三层结构来实现输出层的输出值outputLayer_output,不断逼近给定的y值,从而训练得到一个精准的模型的呢?
从图中串起来的端口,可以想到一个过程:坐地铁,将图一想象为一条地铁线路。王某某坐地铁回家的一天:在input起点站上车,中途经过了很多站(hiddenLayer),然后发现坐过头了(outputLayer对应现在的位置),那么王某某将会根据现在的位置离家(目标Target)的距离(误差Error),返回到中途的地铁站(hiddenLayer)重新坐地铁(误差反向传递,使用梯度下降算法更新w和b),如果王某某又一次发生失误,那么将再次进行这个调整的过程。
从在婴儿拍打桌子和王某某坐地铁的例子中,思考问题:BP的完整训练,需要先传入数据给input,再经过隐含层的映射,输出层得到BP仿真值,根据仿真值与目标值的误差,来调整参数,使得仿真值不断逼近目标值。比如(1)婴儿受到了外界的干扰因素(x),从而作出反应拍桌(predict),大脑不断的调整胳膊位置,控制四肢拍准(y、Target)。(2)王某某上车点(x),过站点(predict),不断返回中途站来调整位置,到家(y、Target)。
在这些环节中,涉及了影响因素数据x,目标值数据y(Target)。根据x,y,使用BP算法来寻求x与y之间存在的规律,实现由x来映射逼近y,这就是BP神经网络算法的作用。再多说一句,上述讲的过程,都是BP模型训练,那么最终得到的模型虽然训练准确,但是找到的规律(bp network)是否准确与可靠呢。于是,我们再给x1到训练好的bp network中,得到相应的BP输出值(预测值)predict1,通过作图,计算Mse,Mape,R方等指标,来对比predict1和y1的接近程度,就可以知道模型是否预测准确。这是BP模型的测试过程,即实现对数据的预测,并且对比实际值检验预测是否准确。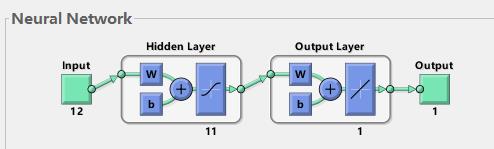
图一 3层BP神经网络结构图
1.2 基于历史值影响的BP神经网络
以电力负荷预测问题为例,进行两种模型的区分。在预测某个时间段内的电力负荷时:
一种做法,是考虑 t 时刻的气候因素指标,比如该时刻的空气湿度x1,温度x2,以及节假日x3等的影响,对 t 时刻的负荷值进行预测。这是前面1.1所说的模型。
另一种做法,是认为电力负荷值的变化,与时间相关,比如认为t-1,t-2,t-3时刻的电力负荷值与t时刻的负荷值有关系,即满足公式y(t)=F(y(t-1),y(t-2),y(t-3))。采用BP神经网络进行训练模型时,则输入到神经网络的影响因素值为历史负荷值y(t-1),y(t-2),y(t-3),特别地,3叫做自回归阶数或者延迟。给到神经网络中的目标输出值为y(t)。
二、海鸥算法
海鸥算法主要模拟了海鸥的迁徙行为和攻击行为 。迁徙行为即海鸥从一个现阶段不适宜生存的地方飞往另一个适宜生存的地方,迁徙行为影响着SOA算法的全局探索能力;攻击行为即海鸥在飞行过程中对地面、水域内食物的攻击觅食,攻击行为影响着SOA算法的局部开发能力。
2. SOA算法流程
2.1 迁徙行为(exploration ability)

2.2 攻击行为(exploitation ability)

2.3 SOA算法流程

三、部分代码
%%% Designed and Developed by Dr. Gaurav Dhiman (http://dhimangaurav.com/) %%%
function[Score,Position,Convergence]=SOA(Search_Agents,Max_iterations,Lower_bound,Upper_bound,dimension,objective)
Position=zeros(1,dimension);
Score=inf;
Positions=init(Search_Agents,dimension,Upper_bound,Lower_bound);
Convergence=zeros(1,Max_iterations);
l=0;
while l<Max_iterations
for i=1:size(Positions,1)
Flag4Upper_bound=Positions(i,:)>Upper_bound;
Flag4Lower_bound=Positions(i,:)<Lower_bound;
Positions(i,:)=(Positions(i,:).*(~(Flag4Upper_bound+Flag4Lower_bound)))+Upper_bound.*Flag4Upper_bound+Lower_bound.*Flag4Lower_bound;
fitness=objective(Positions(i,:));
if fitness<Score
Score=fitness;
Position=Positions(i,:);
end
end
Fc=2-l*((2)/Max_iterations);
for i=1:size(Positions,1)
for j=1:size(Positions,2)
r1=rand();
r2=rand();
A1=2*Fc*r1-Fc;
C1=2*r2;
b=1;
ll=(Fc-1)*rand()+1;
D_alphs=Fc*Positions(i,j)+A1*((Position(j)-Positions(i,j)));
X1=D_alphs*exp(b.*ll).*cos(ll.*2*pi)+Position(j);
Positions(i,j)=X1;
end
end
l=l+1;
Convergence(l)=Score;
end
四、仿真结果
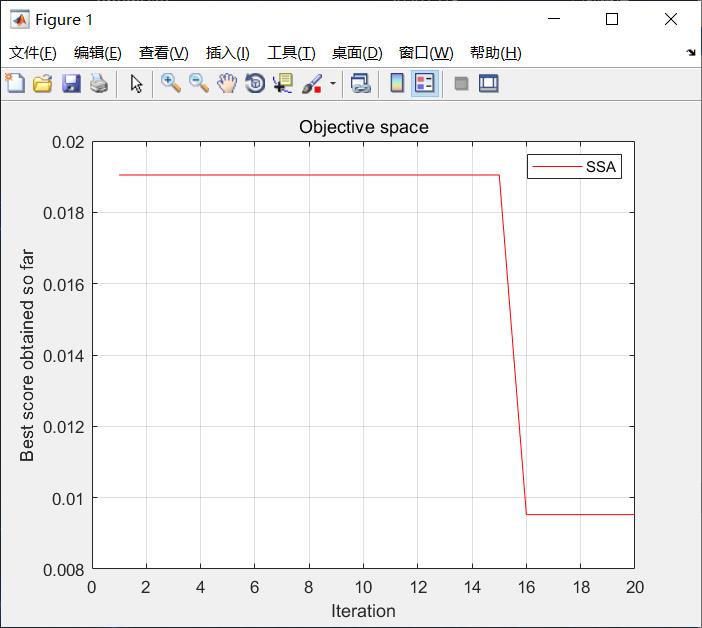
图2海鸥算法收敛曲线
测试统计如下表所示
| 测试结果 | 测试集正确率 | 训练集正确率 |
|---|---|---|
| BP神经网络 | 100% | 95% |
| SOA-BP | 100% | 99.8% |
五、参考文献及代码私信博主
《基于BP神经网络的宁夏水资源需求量预测》

以上是关于BP神经网络预测(python)的主要内容,如果未能解决你的问题,请参考以下文章