Apriori 实现关联分析

Posted 2022-11-20 Debroon

通过 Apriori 实现关联分析

• • 关联分析
  • • 最小支持度
    • 最小置信度
    • Apriori 算法
    • apriori 函数
    • 商品零售购物篮分析
    • 公众号文章关联分析

 

---

关联分析

沃尔玛超市在对顾客的购物记录进行购物篮分析时，发现了一个奇怪的现象： “啤酒”和“尿布”两件看上去毫无关系的商品，经常出现在同一个购物篮中。

随后，他们深入分析，发现这种奇怪的现象大多发生在年轻的父亲身上，原因是父亲在购买婴儿尿片时，通常会捎带几瓶啤酒犒劳自己。

于是，沃尔玛调整了货架，尝试将啤酒和尿布摆在一个区域，方便顾客购买，从而提升了超市的销量。

关联分析可以让我们从数据集中发现项与项之间的关系，它在我们的生活中有很多应用场景，“购物篮分析”就是一个常见的场景，这个场景可以从消费者交易记录中发掘商品与商品之间的关联关系，进而通过商品捆绑销售或者相关推荐的方式带来更多的销售量。

我们通过 Apriori算法 实现关联分析：

• 消费市场瞄准目标客户，猜测这些年来顾客的消费习惯，减少广告预算和增加收入。
• 股票数据挖掘，发现相关性。
• 安全领域，降低火灾事故隐患。
• 网络安全领域，网络入侵检测技术。
• 高校管理，高校大量贫困生人数的补助。
• 生物信息学，大数据个性化治疗癌症、功能基因定位。
• 地球科学，发现各种自然力之间的相互作用。
• ······
   

---

最小支持度

• 支持度：$X、Y的支持度=\frac{X、Y出现的次数}{事物出现的总次数}$

支持度是百分比，同时购买 X、Y 的订单数占总订单数的比例。

支持度越高，代表这个组合出现的频率越大。

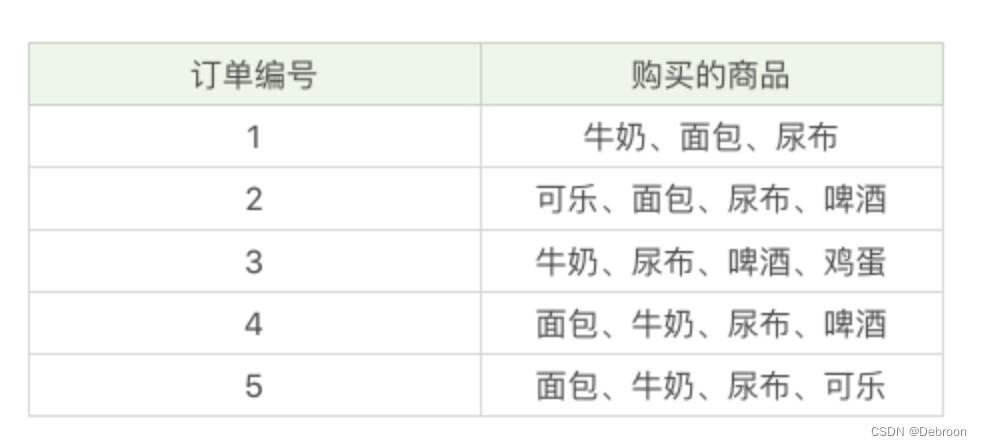
在这个例子中，我们能看到“牛奶”出现了 4 次，那么这 5 笔订单中“牛奶”的支持度就是 $\frac{4}{5}=0.8$。

• $牛奶的支持度=\frac{牛奶出现的次数}{所有事物出现的总次数}=\frac{4}{5}=0.8$

同样“牛奶 + 面包”出现了 3 次，那么这 5 笔订单中“牛奶 + 面包”的支持度就是 $\frac{3}{5}=0.6$。

• $牛奶+面包的支持度=\frac{牛奶+面包出现的次数}{所有事物出现的总次数}=\frac{3}{5}=0.6$

基于这份数据，数据分析师可向老板提出建议，推出 $牛奶+面包$ 的组合套餐。

因为我们发现购买牛奶的用户，有很大概率会加购面包。

······

为了后续学习，我们来介绍一些名词。

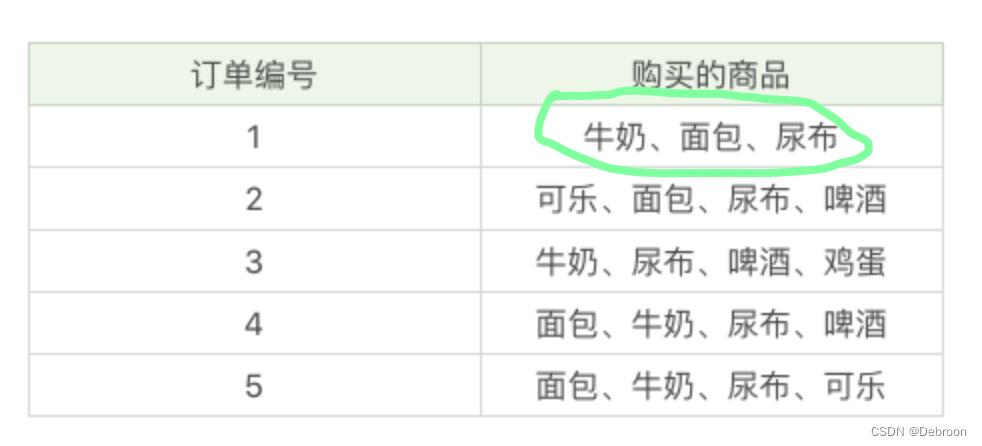
每条交易记录又可称为一个事务（上图绿色），一共有 5条 事物。

交易中的不同物品可称为一个项，一共 5 项：牛奶、面包、尿布、啤酒、可乐。

0个或多个项的集合，可称为一个项集，一般用X的形式表示项集，k 个项组成的项集，叫 k 项集。

• 一个 $k$ 项 的数据集，能产生 $2^k-1$ 个非空频繁项集

如：薯条，可乐 是 2 项集，薯条 是 1 项集。

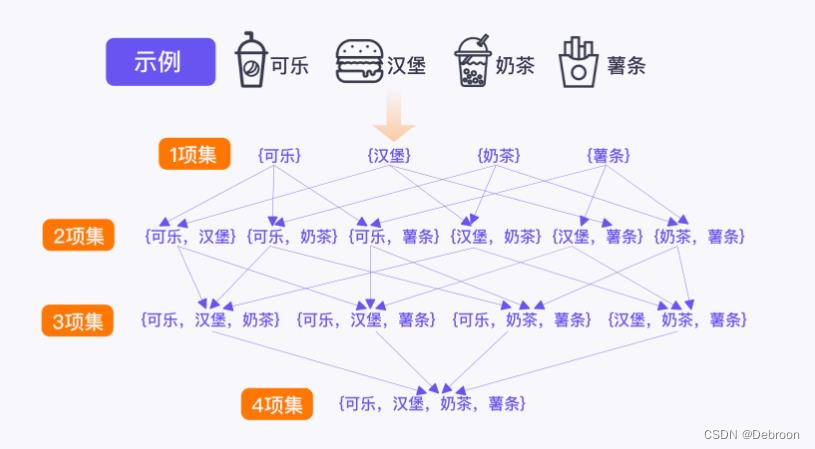
不同“项集”，受顾客的欢迎程度不同。

支持度可以表示项集在事务中出现的概率，也可以理解成顾客对某一个项集的“支持程度”。

每个项集都有支持度，但事实上，也不是每个项集都是有用的。

假设 4 项集：可乐，汉堡，奶茶，薯条 支持度为 $0$，客人都没买过这样的套餐，就没有指导价值。

此时，我们需要人为地设定一个支持度 m，名为最小支持度，用于筛掉那些不符合需求的项集。

• 被留下来的项集（≥ 最小支持度 m），被称为频繁项集。

有了频繁项集，就可以生产关联规则了。

数据之间的联系，我们用关联规则来表示，表达式为：$X\to Y$（X 和 Y 之间不存在相同项）。

规则有顺序之分，为了方便描述，我们把规则前面的项集叫前件，把规则后面的项集叫后件。

• 一个 $k$ 项 的频繁项集，可产生 $2^k-2$ 个关联规则。

数据之间的联系，我们用关联规则来表示，表达式为：前件X→后件Y。

假设有频繁项集 牛奶，面包，可以生成 2 条关联规则：牛奶→薯条、面包→牛奶，我们猜测他们之间存在某种联系。

我们需要衡量这种关系是否可靠？如果可靠，到底有多可靠？哪个更可靠？
 

---

最小置信度

置信度：$关联规则X\to Y的置信度=\frac{X,Y的支持度}{X的支持度}$

置信度用于衡量关联规则的可靠程度，表示在前件出现的情况下，后件出现的概率。

• 牛奶→薯条，购买“牛奶”的顾客，再购买“面包”的概率
• 面包→牛奶，购买“面包”的顾客，再购买“牛奶”的概率

在前件出现的情况下，后件出现的概率。

同为关联规则，可靠程度有“强”、有“弱”。

在实际业务中，也需要人为地设定置信度 n，名为最小置信度，用于筛掉一些不符合需求的关联规则。

被留下来的关联规则（ ≥ 最小置信度 n），叫做强关联规则。

关联规则也一样，既有促进关系，也有抑制关系。

因而，还需引入提升度对它们进行判断。
 

---

提升度：$X\to Y的提升度=\frac{X\to Y的置信度}{Y的支持度}$

意思是 X 的出现，对 Y 出现的影响有多大，商品 X、Y 的相关性。

• 提升度 > 1，前件对后件是促进关系
• 提升度 = 1，前件不影响后件
• 提升度 < 1，前件对后件是抑制关系

随着“项”的增加，频繁项集和关联规则的计算量必将呈指数增长。

而现实生活中的“项”（商品）成百上千，真实的“事务”（交易）数以万计。

提高计算效率，就用 Apriori 算法。
 

---

Apriori 算法

Apriori 算法分为俩步：

• 确定最小支持度和最小置信度

按照经验先猜一个数，最小支持度0.2、最小置信度0.7。

• 找出所有频繁项集和强关联规则

在 Apr 算法出现之前，要找出所有的频繁项集，就得先枚举所有的项集，计算它们的支持度，筛选出频繁项集（> 0.2）。

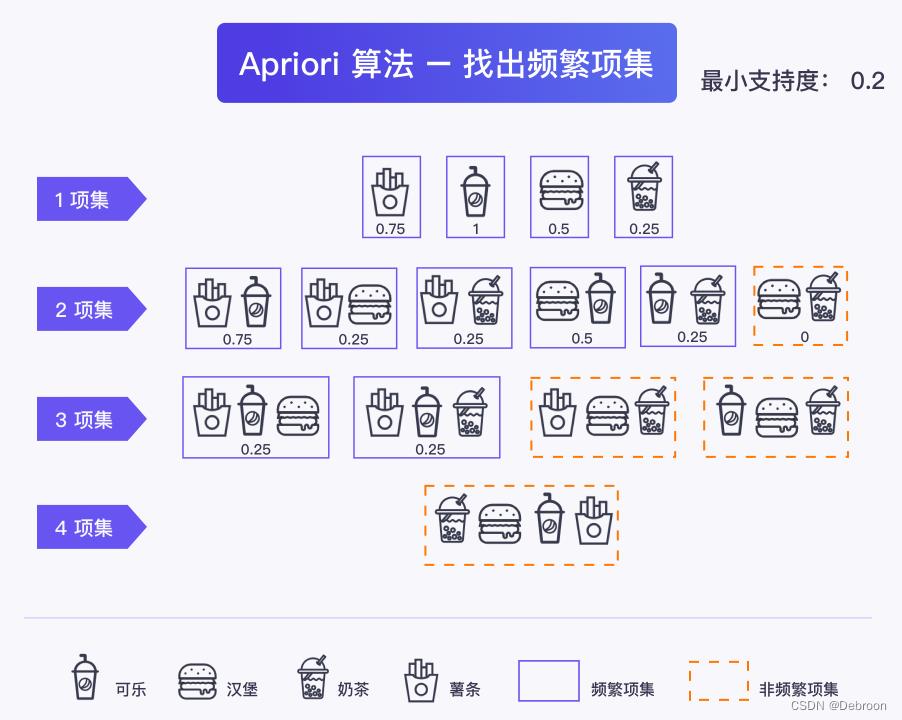
算法的优化，在于不做无用功，减少不必要的重复。

• 一个项集如若是频繁的，那它的非空子集也一定是频繁的。

购买薯条，奶茶的概率都很高，那购买薯条或奶茶的概率肯定也很高。

• 一个项集如若是非频繁的，那包含该项集的项集也一定是非频繁的。

假设购买薯条的次数少，那购买薯条，奶茶的次数肯定也少。

Apriori 算法的思路是，一旦找到某个不满足条件的“非频繁项集”，包含该集合的其他项集不需要计算，更不用对比，通通绕开。

比如，在对比 2 项集的时候，发现奶茶，汉堡的支持度为 0，小于最小支持度0.2，属于非频繁项集。

于是，后面在计算3项集、4项集 ····· 最后项集的时候，会直接把包含奶茶，汉堡的项集，如薯条，奶茶，汉堡、薯条，奶茶，汉堡，可乐去掉，不再计算。

• 一项集：薯条、可乐、汉堡、奶茶
• 二项集：薯条、可乐、薯条、汉堡、薯条、奶茶、汉堡、可乐、可乐、奶茶
• 三项集：薯条、可乐、汉堡、薯条、可乐、奶茶

因为一项集只有一个项，无法构成具有指导意义的关联关系（≥ 2 项），可直接忽略。

• 二项集：薯条、可乐、薯条、汉堡、薯条、奶茶、汉堡、可乐、可乐、奶茶
• 三项集：薯条、可乐、汉堡、薯条、可乐、奶茶

根据二、三项集新生成的频繁项集：

Apr 算法会先产生一系列后件项数为 1 的关联规则，与最小置信度进行比较：

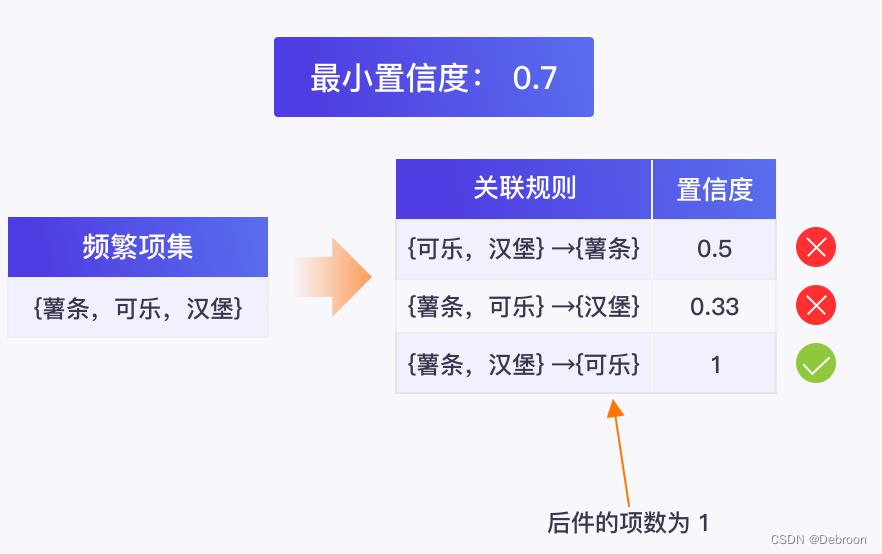
频繁项集继续生成后件的项数为 2 的关联规则，再对它们的置信度进行比较：

当无法从剩下的频繁项集中生成新的关联规则时，该过程就结束了。

通过这种方式，其他的频繁项集也加入到关联规则的“生产线”上，最终通过最小置信度筛选，就算“牵手”成功，得到强关联规则如下：

若是这些强关联规则正好是你想要的，那就进一步计算它们的提升度，研究俩者的关系是抑制，还是促进。

若是对筛选出来的强关联规则不满意，那我们就得重新调整最小支持度和最小置信度，再计算一次。

 

---

apriori 函数

Python 把 Apr 算法的计算流程抽象成函数，将最小支持度、最小置信度和最小提升度设置成参数，通过调整参数来查看关联规则。

from efficient_apriori import apriori
# 导入 apyori 模块下的 apriori 函数
data = [['薯条', '可乐'], ['薯条', '可乐', '奶茶'], ['汉堡', '薯条', '可乐'], ['汉堡', '可乐']]
# 创建 4 条快餐交易数据
itemsets, rules = apriori(data, min_support=0.2,  min_confidence=0.7, min_lift=1)
# data 数据集
# min_support 最小支持度，用户更有可能购买的商品（频繁项集）
# min_confidence 最小置信度，用户在买某商品的时候，更倾向或者更不倾向购买的另外一个商品（强关联规则）
# min_lift 最小提升度，去除存在抑制关系（1）的强关联规则，用户在买某商品的时候，可能会继续购买的另外一个商品

 

---

商品零售购物篮分析

购物篮分析，是关联分析的一种重要应用。

通过发现顾客在一次购买行为中放入购物篮的不同商品之间的关联，研究客户的购买习惯，从而辅助零售企业制定营销策略。

 

---

公众号文章关联分析

 

---