机器学习python实现吴恩达机器学习作业合集(含数据集)
Posted —Xi—
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习python实现吴恩达机器学习作业合集(含数据集)相关的知识,希望对你有一定的参考价值。
学习感言:
从3.7第一天开始,到今天4.4,一个多月的时间,陆续完成了听课,代码实现和总结博客,过程些许艰难,作为一个刚入门的学习者,收获了很多。总结一下这一段时间的学习过程吧。后面的学习方向还在思考。
目录
作业涉及到的数据集:
之前的数据集过期了,重新更新
链接:https://pan.baidu.com/s/14gmrdWvIYopPWK_qsJHq5w?pwd=ifuf
提取码:ifuf
Ng课程大纲总结
无监督学习
线性规划,逻辑回归,神经网络,SVM
无监督学习
K-means , PCA , 异常检测
应用
推荐系统,
大规模机器学习
映射化简和数据并行:
将我们的数据集分配给不多台 计算机,让每一台计算机处理数据集的一个子集,然后我们将计所的结果汇总在求和。这样 的方法叫做映射简化。如果任何学习算法能够表达为,对训练集的函数的求和,那么便能将这个任 务分配给多台计算机(或者同一台计算机的不同 CPU 核心),以达到加速处理的目的。
构建机器学习系统tips
方差/偏差 ,正则化
决定下一步做什么:
算法评估,学习曲线(判断高偏差/高方差问题),误差分析
上限分析:机器学习的应用中,我们通常需要通过几个步骤才能进行最终的预测,我们如何能够 知道哪一部分最值得我们花时间和精力去改善呢?这个问题可以通过上限分析来回答。
问题描述和流程图
滑动窗口分类算法(CV)
获取大量数据和人工数据
以下是零碎:
现有的机器学习种类繁多,我们一般可以进行如下的分类标准:
- 是否在人类监督下学习(监督学习、非监督学习、半监督学习和强化学习)
- 是否可以动态的增量学习(在线学习和批量学习)
- 是简单的将新的数据点和已知的数据点进行匹配,还是像科学家那样对训练数据进行模型检测,然后建立一个预测模型(基于实例的学习和基于模型的学习)
一 、监督学习与无监督学习
-
监督学习(Supervised Learning):对于数据集中每一个样本都有对应的标签,包括回归(regression)和分类(classification);
- K近邻算法
- 线性回归
- logistic回归
- 支持向量机(SVM)
- 决策树和随机森林
- 神经网络
-
无监督学习(Unsupervised Learning):数据集中没有任何的标签,包括聚类(clustering),著名的一个例子是鸡尾酒晚会。实现公式:[W,s,v] = svd((repmat(sum(x.*x,1),size(x,1),1).*x)*x’);
- 聚类算法
- K均值算法(K-means)
- 基于密度的聚类方法(DBSCAN)
- 最大期望算法
- 可视化和降维
- 主成分分析(PCA)
- 核主成分分析
- 关联规则学习
- Apriori
- Eclat
- 异常检测
-
半监督学习 有些算法可以处理部分标记的训练数据,通常是大量未标记的数据和少量标记的数据,这种成为半监督学习。
-
如照片识别就是很好的例子。在线相册可以指定识别同一个人的照片(无监督学习),当你把这些同一个人增加一个标签的后,新的有同一个人的照片就自动帮你加上标签了。
-
强化学习
强化学习,它的学习系统能够观测环境,做出选择,执行操作并获得回报,或者是以负面回报的形式获得惩罚。它必须自行学习什么是最好的策略,从而随着时间推移获得最大的回
二、在线学习
如果你有一个由连续的用户流引发的连续的数据流,进入你的网站,你能做的是使用一个在线学习机制,从数据流中学习 用户的偏好,然后使用这些信息来优化一些关于网站的决策。
在线学习算法指的是对数据流而非离线的静态数据集的学习。许多在线网站都有持续不断的用户流,对于每一个用户,网站希望能在不将数据存储到数据库中便顺利地进行算法学习。
- 在线学习:产品搜索界面 产品推荐
三、模型训练及选择(model selection)
可以依据训练误差和测试误差来评估假设hθ(x);
一般来说,我们将数据集划分成训练集(60%)、验证集(20%)和测试集(20%);
训练集
训练集用来训练模型,学习参数θ :minJ(θ);即确定模型的权重和偏置这些参数,通常我们称这些参数为学习参数。
验证集
验证集用于模型的选择,更具体地来说,验证集并不参与学习参数的确定,也就是验证集并没有参与梯度下降的过程。用训练集对模型训练完毕后,再用验证集对模型测试,测试模型是否准确而不是训练模型的参数。
测试集
测试集只使用一次,即在训练完成后评价最终的模型时使用。它既不参与学习参数过程,也不参数超参数选择过程,而仅仅使用于模型的评价。
不能在训练过程中使用测试集,而后再用相同的测试集去测试模型。这样做其实是一个cheat,使得模型测试时准确率很高。
四、模型优化
欠拟合,高偏差:说明没有很好的拟合训练数据
过拟合,高方差:拟合训练数据过于完美,J(θ)≈0,导致模型的泛化能力很差,对于新样本不能准确预测

五、机器学习系统设计
不对称分类的误差评估(skewed classes)
错误率:有多少比例的西瓜被判断错误;
查准率(precision):算法挑出来的西瓜中有多少比例是好西瓜;
查全率(recall):所有的好西瓜中有多少比例被算法跳了出来。
- 如果我们想要比较确信为正例时才判定为正例,那么提高阈值,模型会对应高查准率,低召回率;
- 如果希望避免假阴性,那么降低阈值,模型会对应低查准率,高召回率
六、高级优化算法:
- 共轭梯度算法
- BFGS
- L-BFGS
优点:无需人工选择参数α;运算速度比梯度下降更快
缺点:更加复杂
最后:放一下Ng的结语,激励自己继续前进吧~ 感谢老师

吴恩达机器学习作业_python实现
一,必做部分
import pandas as pd
import numpy as np
import scipy.optimize as opt
import matplotlib.pyplot as plt
from sklearn.metrics import classification_report#这个包是评价报告
def get_X(df):#读取特征
ones = pd.DataFrame({'ones': np.ones(len(df))})#ones是m行1列的dataframe
data = pd.concat([ones, df], axis=1) # 合并数据,根据列合并
return data.iloc[:, :-1].values
def get_y(df):#读取标签
return np.array(df.iloc[:, -1])#df.iloc[:, -1]是指df的最后一列
def normalize_feature(df):
return df.apply(lambda column: (column - column.mean()) / column.std())#特征缩放
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def cost(theta, X, y):
return np.mean(-y * np.log(sigmoid(X @ theta)) - (1 - y) * np.log(1 - sigmoid(X @ theta)))
def gradient(theta, X, y):
return (1 / len(X)) * X.T @ (sigmoid(X @ theta) - y)
def predict(x, theta):
prob = sigmoid(x @ theta)
return (prob >= 0.5).astype(int)#.astype方法前的数据类型为numpy.ndarray
theta=np.zeros(3)
data = pd.read_csv('ex2data1.txt', names=['exam 1', 'exam 2', 'admitted'])
X = get_X(data)
y = get_y(data)
res = opt.minimize(fun=cost, x0=theta, args=(X, y), method='Newton-CG', jac=gradient)
'''func:优化的目标函数
x0:初值
fprime:提供优化函数func的梯度函数,不然优化函数func必须返回函数值和梯度,或者设置approx_grad=True
args:元组,是传递给优化函数的参数'''
final_theta = res.x#res.x is final theta
y_pred = predict(X, final_theta)
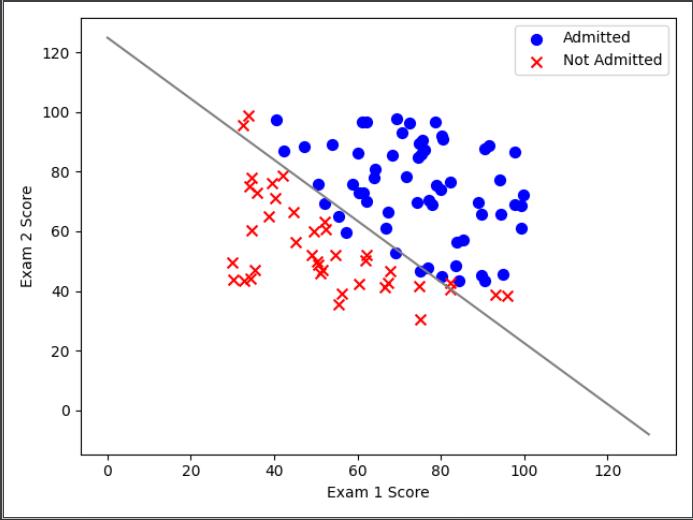
#二维图
positive = data[data['admitted'].isin([1])]
negative = data[data['admitted'].isin([0])]
plt.scatter(positive['exam 1'], positive['exam 2'], s=50, c='b', marker='o', label='Admitted')
plt.scatter(negative['exam 1'], negative['exam 2'], s=50, c='r', marker='x', label='Not Admitted')
plt.legend(loc=0)#增加图例,0,1,2,3,4分别表示不同的位置
plt.xlabel('Exam 1 Score')
plt.ylabel('Exam 2 Score')
coef = -(res.x / res.x[2]) # find the equation
x = np.arange(130, step=0.1)
y2 = coef[0] + coef[1]*x#y = theta@X = sigmod(theta[0]*X[0]+theta[1]*X[1]+theta[2]*X[2])
plt.plot(x, y2, 'grey')
plt.show()
#三维图,注释掉了,看三维效果把下面的注释去掉,49-60加注释
"""x = plt.axes(projection='3d')
ax.scatter(X[:,1], X[:,2], y, alpha=0.3)
D = final_theta[0]
A = final_theta[1]
B = final_theta[2]
Z = A*X[:,1] + B*X[:,2] + D
ax.plot_trisurf(X[:,1], X[:,2], Z,
linewidth=0, antialiased=False,color='r')
ax.set_zlim(-2,2);"""
print(classification_report(y, y_pred))
二,选作部分
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.optimize as opt
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def cost(theta, X, y, learningRate):
theta = np.mat(theta)
X = np.mat(X)
y = np.mat(y)
first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))
reg = (learningRate / (2 * len(X))) * np.sum(np.power(theta[:,1:theta.shape[1]], 2))
return np.sum(first - second) / len(X) + reg
def gradientReg(theta, X, y, learningRate):
theta = np.mat(theta)
X = np.mat(X)
y = np.mat(y)
parameters = int(theta.ravel().shape[1])
grad = np.zeros(parameters)
error = sigmoid(X * theta.T) - y
for i in range(parameters):
term = np.multiply(error, X[:, i])
if (i == 0):
grad[i] = np.sum(term) / len(X)
else:
grad[i] = (np.sum(term) / len(X)) + ((learningRate / len(X)) * theta[:, i])
return grad
def predict(theta, X):
probability = sigmoid(X * theta.T)
return [1 if x >= 0.5 else 0 for x in probability]
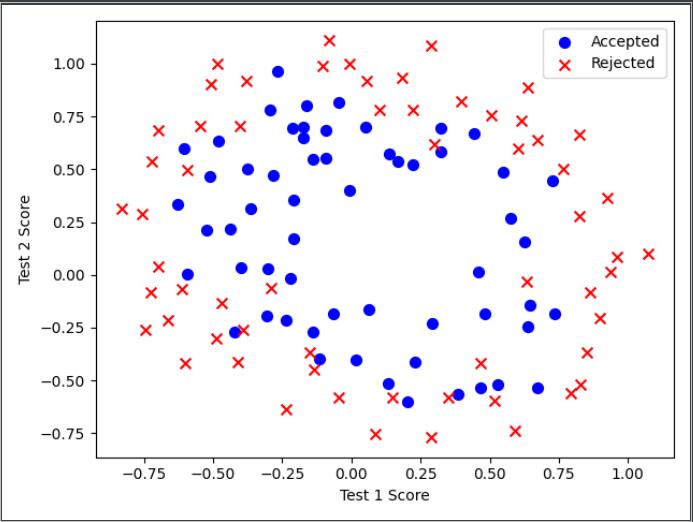
data2 = pd.read_csv("ex2data2.txt", header=None, names=['Test 1', 'Test 2', 'Accepted'])
df = data2[:]
#原始数据
positive = data2[data2['Accepted'].isin([1])]
negative = data2[data2['Accepted'].isin([0])]
plt.scatter(positive['Test 1'], positive['Test 2'], s=50, c='b', marker='o', label='Accepted')
plt.scatter(negative['Test 1'], negative['Test 2'], s=50, c='r', marker='x', label='Rejected')
plt.legend()
plt.xlabel('Test 1 Score')
plt.ylabel('Test 2 Score')
plt.show()
degree = 5
x1 = data2['Test 1']
x2 = data2['Test 2']
data2.insert(3, 'Ones', 1)#插入在第三列之前
for i in range(1, degree):#i:1~4
for j in range(0, i):#i=4时,j为0到3
data2['F' + str(i) + str(j)] = np.power(x1, i-j) * np.power(x2, j)
'''将F10,F20,F21这些列加在data2的最后,例如:data["ww"]=1 会在data2的列之后在格外加一列名字为ww'''
data2.drop('Test 1', axis=1, inplace=True)#删除方法,将index为Test 1,axis=1说明删除的是列
data2.drop('Test 2', axis=1, inplace=True)#如果手动设定为True(默认为False),那么原数组直接就被替换
#而采用inplace=False之后,原数组名对应的内存值并不改变,需要将新的结果赋给一个新的数组或者覆盖原数组的内存位置
cols = data2.shape[1]
X2 = data2.iloc[:, 1:cols].values#删除accepted列
y2 = data2.iloc[:, 0:1].values#仅保留accepted列
theta2 = np.zeros(11)
learningRate = 1
final_theta = opt.fmin_tnc(func=cost, x0=theta2, fprime=gradientReg, args=(X2, y2, learningRate))
'''或用
res = opt.minimize(fun=cost,
x0=theta2,
args=(X2, y2, learningRate),
method='TNC',
jac=gradientReg)
final_theta = res.x可得到相同的结果
func:优化的目标函数
x0:初值
fprime:提供优化函数func的梯度函数,不然优化函数func必须返回函数值和梯度,或者设置approx_grad=True
args:元组,是传递给优化函数的参数
'''
theta_min = np.mat(final_theta[0])
predictions = predict(theta_min, X2)
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y2)]
accuracy = (sum(map(int, correct)) % len(correct))
print('accuracy = {0}%'.format(accuracy))
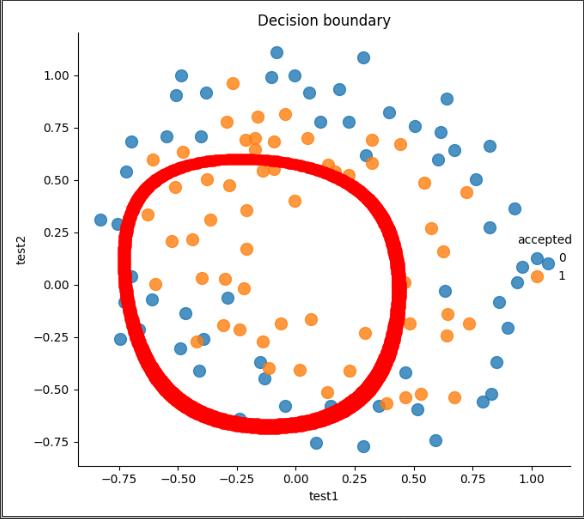
原始数据如图
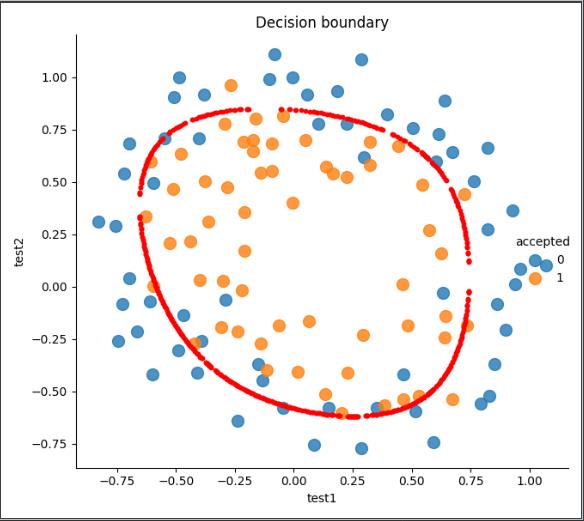
画出决策边界:由于𝑋×𝜃是个11维的图,我们不能直观的表示出来
但可以找到所有 𝑋×𝜃近似等于0的值以此来画出决策边界(是这么个思路,以下复制了国外大牛的代码)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.optimize as opt
import seaborn as sns
def cost(theta, X, y):
return np.mean(-y * np.log(sigmoid(X @ theta)) - (1 - y) * np.log(1 - sigmoid(X @ theta)))
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def gradient(theta, X, y):
return (1 / len(X)) * X.T @ (sigmoid(X @ theta) - y)
def feature_mapping(x, y, power, as_ndarray=False):
data = {"f{}{}".format(i - p, p): np.power(x, i - p) * np.power(y, p)
for i in np.arange(power + 1)
for p in np.arange(i + 1)
}
if as_ndarray:
return pd.DataFrame(data).values
else:
return pd.DataFrame(data)
def regularized_gradient(theta, X, y, l=1):
# '''still, leave theta_0 alone'''
theta_j1_to_n = theta[1:]
regularized_theta = (l / len(X)) * theta_j1_to_n
# by doing this, no offset is on theta_0
regularized_term = np.concatenate([np.array([0]), regularized_theta])
return gradient(theta, X, y) + regularized_term
def regularized_cost(theta, X, y, l=1):
# '''you don't penalize theta_0'''
theta_j1_to_n = theta[1:]
regularized_term = (l / (2 * len(X))) * np.power(theta_j1_to_n, 2).sum()
return cost(theta, X, y) + regularized_term
def feature_mapped_logistic_regression(power, l):
df = pd.read_csv('ex2data2.txt', names=['test1', 'test2', 'accepted'])
x1 = np.array(df.test1)
x2 = np.array(df.test2)
y = np.array(df.iloc[:, -1])
X = feature_mapping(x1, x2, power, as_ndarray=True)
theta = np.zeros(X.shape[1])
res = opt.minimize(fun=regularized_cost,
x0=theta,
args=(X, y, l),
method='TNC',
jac=regularized_gradient)
final_theta = res.x
return final_theta
def find_decision_boundary(density, power, theta, threshhold):
t1 = np.linspace(-1, 1.5, density)
t2 = np.linspace(-1, 1.5, density)
cordinates = [(x, y) for x in t1 for y in t2]
x_cord, y_cord = zip(*cordinates)
mapped_cord = feature_mapping(x_cord, y_cord, power) # this is a dataframe
inner_product = mapped_cord.values @ theta
decision = mapped_cord[np.abs(inner_product) < threshhold]
return decision.f10, decision.f01
def draw_boundary(power, l):
density = 1000
threshhold = 2 * 10**-3
final_theta = feature_mapped_logistic_regression(power, l)
x, y = find_decision_boundary(density, power, final_theta, threshhold)
df = pd.read_csv('ex2data2.txt', names=['test1', 'test2', 'accepted'])
sns.lmplot('test1', 'test2', hue='accepted', data=df, size=6, fit_reg=False, scatter_kws={"s": 100})
plt.scatter(x, y, color='red', s=10)
plt.title('Decision boundary')
plt.show()
draw_boundary(6, 1)#第二个为lambda的值,lambda=0过拟合,lambda=100欠拟合
过拟合:draw_boundary(6, 0)
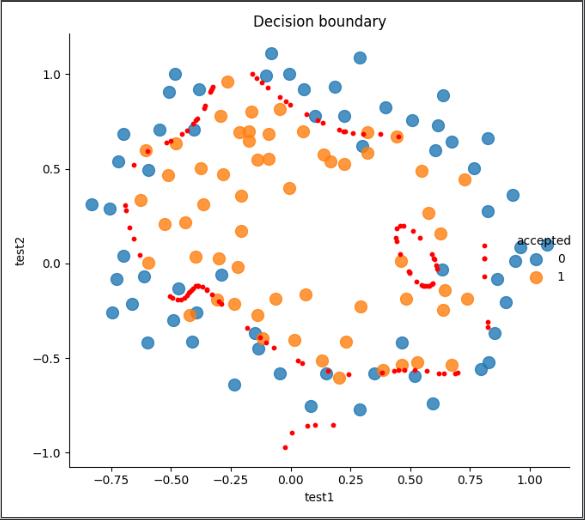
欠拟合:draw_boundary(6, 100)
以上是关于机器学习python实现吴恩达机器学习作业合集(含数据集)的主要内容,如果未能解决你的问题,请参考以下文章