POE 利用区块链挖掘协同执行遗传算法
Posted 夏虫不可语冰也
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了POE 利用区块链挖掘协同执行遗传算法相关的知识,希望对你有一定的参考价值。
论文地址
Proof of Evolution: leveraging blockchain mining for a cooperative execution of Genetic Algorithms
带着问题去阅读:
- 什么是进化证明?
- 进化证明有什么优点,从哪些角度去证明该方法的正确性?
- 进化证明有什么缺点,哪些原因被限制住了,有什么方法能解决这些问题?
- 未来的方向
核心思想
POE与POW和POS的区别与联系
使用部分挖矿组件来执行一些客户可以提交的遗传算法(GA)
PoE实现了矿工之间的一种合作心思。在采矿过程中,矿工必须维护和发展候选解决方案的群体,PoE为他们提供了分享他们当前发现的最佳解决方案的可能性,他们可以将这些解决方案添加到他们的群体中。
PoW的优势,只要诚实的节点集体控制的计算能力超过任何合作的攻击者节点群,该系统就可以被认为是安全的。这种说法建立在矿工必须解决散列难题的属性,以实例化一个区块。
上述属性包括:
- 问题的内在硬度
- 容易解决的公共可验证性
- 所有问题的同质硬度
- 难度可调整性
- 区块敏感性
- 不可重复使用性
- 计算的独立同分布性
PoW的缺点:为了保持区块链运行引起的巨大消耗。
本文贡献
- PoE能在采矿时执行优化问题,并且包含了PoW的所有属性,它通过在采矿过程中消耗的部分计算能力来执行GA,使矿工之间进行合作,提高GA的解决方案的质量。
- 提供来一个关于工作在采矿计算总量中的百分比估计,实验结果表明使用PoE达成的解决方案质量优于用PoS达成的结果。
nonce的结构
- nonce("sol","eval","cmp")
- sol:使用中的GA的可能解决方案
- eval:精确性
- cmp:衡量所使用的精确性函数的复杂性 nonce的结构
在 PoE 的 nonce 第三个值与作业的解决方案及其评估一起要求。
每个基本操作都有自己的去权重,而且这些权重不是固定,会被一个伪随机变量所改变,这个偏移量由前一个区块的哈希值和矿工的公钥决定。
如何引入合作?
矿工应该能够分享他们的解决方案,使其他们无法窃取他们。 在PoS中, 这个问题是可以避免的,因为只有宣布最佳解决方案的矿工才会在比赛结束时公布其解决方案。
PoE中,矿工想分享他们当前的最佳解决方案:
- 检查他们的解决方案所属的工作是否开放
- 检查他们的解决方案是否优于已知的最佳解决方案
- 在交易中提交解决方案时,ID以及通过评估器获得的解决方案的分数连接哈希值
- 等到当前区块被开采出来,这样他们之前的交易就被确认了
- 其他矿工可以将解决方案添加到他们的本地群里中,并使用它进行交叉,如果他们发现了更好的解决方案
奖励
PoE有三种不同的独立奖励:
- 对发现有效nonce的第一个矿工的奖励
- 对客户提交的GA最佳解决方案的矿工的奖励
- 以及对激励矿工合作的奖励
挖矿的奖励由系统分配能够像PoW那样实例化一个区块的第一个矿工。
最佳解决方案的奖励是由提交相应GA的客户支付的,就像在PoS中。这样一来,客户就没有兴趣提交一个他已经知道最佳解决方案的作业,无法作弊。
为了建立一个真正的合作系统,应该刺激矿工分享个人解决方案。因此只要他们的解决方案对其他人有用,他们就应该得到一点奖励。这种奖励不能由系统产生,否则客户可能会赚取欺骗的钱。所以这种奖励也必须由客户支付。系统应该制定一些标准来说明一个解决方案是否“有用”,以确定何时必须向矿工付款。
安全考虑
这个模型中并不鼓励客户为自己的工作提交解决方案,特别是提交他已经知道的好解决方案的工作,因为他必须为使用这个系统付费。
这个恶意的客户端可以建立一个假的评估器,它为他所知道的特定输入返回最大的分数,而为输入中的每一个其他值返回常规的分数。如果矿工在区块链中分享他们的解决方案,客户端可以阅读它们,在比赛结束时,他将成为拥有假的最佳解决方案的赢家,获得他支付的奖金。因此,他将从其他人那里读到一些好的解决方案,而不支付他们。为了防止这种不良行为,PoE要求对有用的共享解决方案也要付费,而且这种付费必须由客户来执行。如果一个客户提交了一个假的最佳解决方案,没有其他的解决方案会更好,因此,从那一刻起,没有更好的解决方案会被公布。
拒绝服务攻击,阻止工作的执行或支付。一种方法是为候选解决方案提交一个虚假的高评价。这种攻击可以被检测到与评估者检查解决方案。执行攻击的节点可以被禁止进入网络,最佳解决方案的选择可以重新开始。
PoW的另一个可能的问题是由挖矿的竞争性质引起的,它促使矿工购买应用规格集成电路形式的定制硬件。这种硬件比一般的硬件更有效,因此更容易使用。
测试和比较
作者将POE和POW以及POS进行了比较。
考虑到给定作业的评估者的复杂性,散列问题的硬度也相应进行了调整。POS(Proof of Search)被设计为使用与POW相同数量级的能量。POE也进行了相应的调整,使其消耗相同数量级的能量。POE与POW最大的不同在于,其在运行时会解决相应的优化问题。
挖矿任务的难易程度是由哈希字符串开头所需的零数来决定。在此我们假设哈希值是以十六进制字符串的形势存储在区块中,给定一个硬度k,随机nonce的有效概率为p=16^(-k).
挖矿有很多不走,矿工在其中生成一个新的nonce并检查其哈希值,知道一个有效的nonce被发现。最终操作量是由所有矿工进行尝试的次数乘以每一次尝试所需操作次数得到。
假设一个POW挖矿任务需要一个硬度k,则称之为:
- 可以调整PoE对一个作业说要求采矿任务的硬度,以便需要与PoW相等的总操作量。
- 如果PoE为一个特定的工作选择的硬度是k-1, 那么在每个采矿点花费的93%的操作尝试是有益的工作。
- 如果PoE为某一特定工作选择的硬度为k-2或者更小,则99%的操作都是有用的。
提出的定理:
将一项工作在POE中的硬度与它的复杂性联系起来。
POE中挖矿任务的硬度y可以通过计算y=k-log16((w+x)/w) w是制作区块哈希的计算要求,k是POW的目标硬度。
如果我们有y=k-1,更与上面的公式我们可以算出x~w(16^1 - 1)=15w。因为在每次采矿中尝试所进行的计算都是w+x=w+15w=16w,每次尝试的有用功百分比为x/(w+x)=15/16~93%
-
IV.1 设k是POW中挖矿任务的硬度,y是POE为使用挖矿过程与POW在总量上一致而应该设置的硬度。设w为POW在每次尝试执行散列和检查时花费的操作量,设x为POE在每次尝试通过评估工作的候选解决方案生成新的nonce时花费的额外操作量。
于是有了下面两条近似结果:
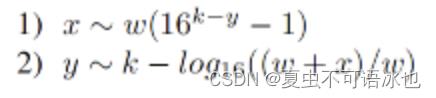
-
在证明IV.1之前,我们还需要证明 IV.2,设Pk为硬度k的采矿过程中哈希有效的概率,a是一个期望的阈值。矿工应该进行多少次尝试N,使得有K>=a的概率发现。一个有效的nonce是
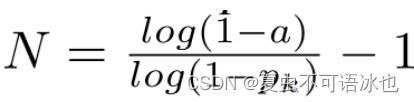
以最简单的方式表达就是:给定一个复杂度为x的工作,有可能找到一个使数量相等的硬度y,反之,给定一个硬度y,有可能得到工作必须具有复杂度x,以使得数量相等。
POE相比较于POS(搜索证明)的优势在于:它可以通过促成矿工之间合作来提高最终解决方案的质量。
通过在两种模式(标准和合作)下执行一套GA,在一组用不同种子初始化的矿工身上执行固定代数。
在这些测试中,一共考虑了4个GAs实现的实例:
- TSP problems (最小化问题)
- Knapsack problems (最大化问题)
- Locolmotion problem (一个调用外部程序的复杂fitness任务)
- Symbolic Regression problem(使用GP编程)
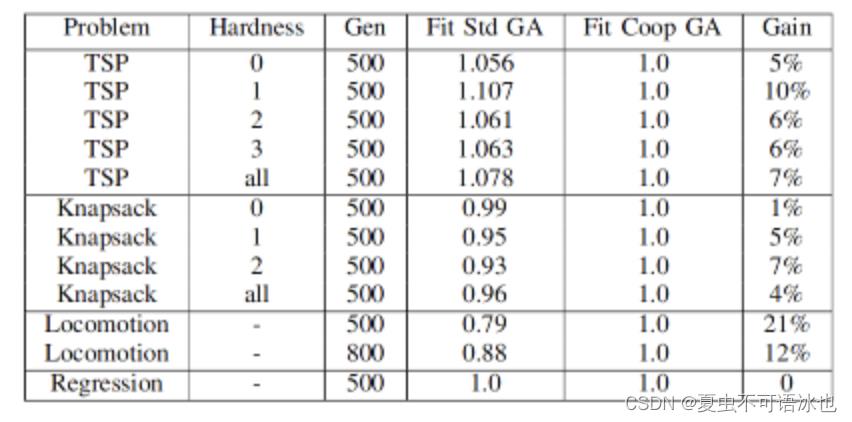
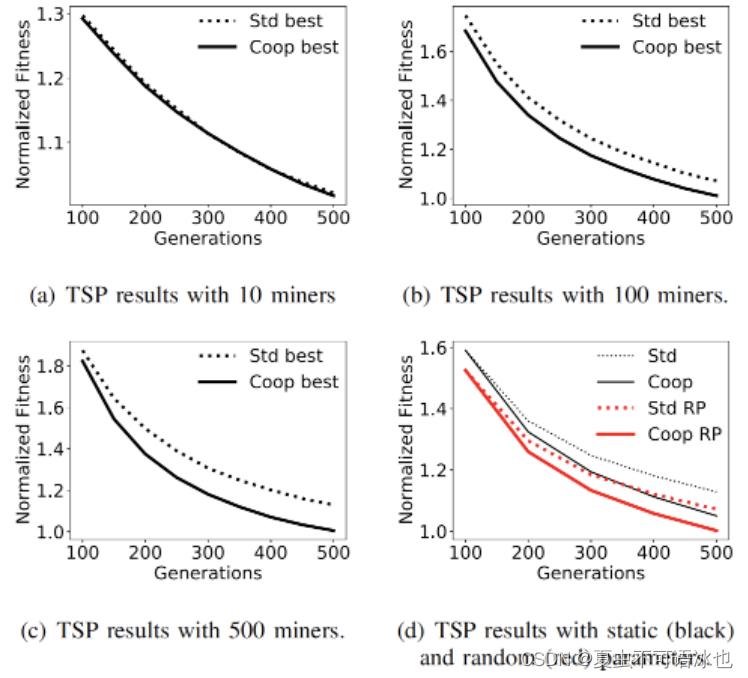
最终实验结果表明,合作可以提高GA的最佳解决方案的精确性。
如果这篇文章对你有所帮助~
欢迎关注我的公众号夏虫不可语冰也
同时也欢迎访问我的个人网站 www.cjl946.com
未来将会出更多区块链相关论文解析哦!

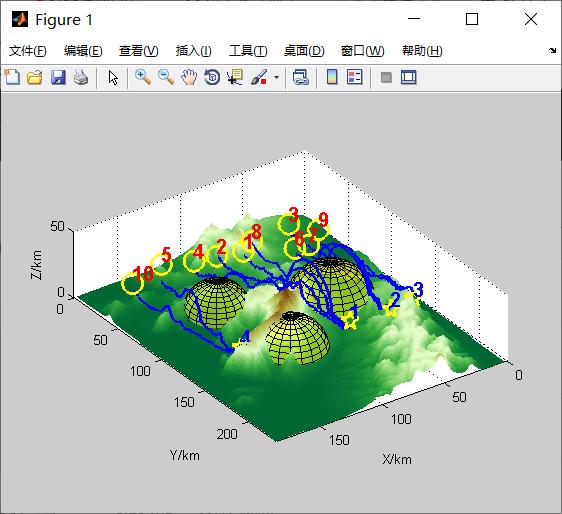
路径规划考虑分配次序的多无人机协同目标分配建模与遗传算法求解
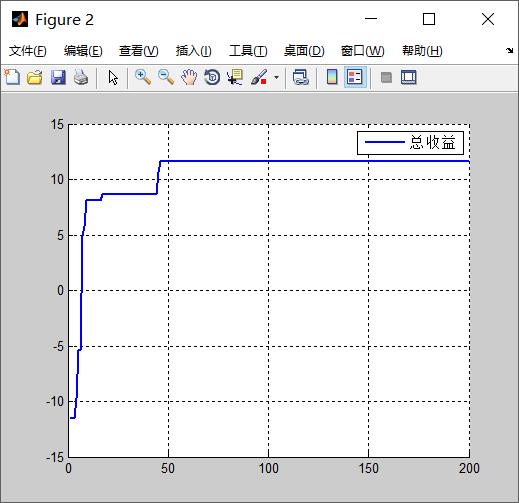
首先通过分析UAV分配次序对打击任务总收益的影响, 设计了动态战场环境的更新规则. 将航程代价和任务代价作为惩罚项修正目标函数, 建立了考虑分配次序的UAVs协同目标分配优化模型. 然后针对模型的物理意义改进了遗传算法基因编码方式, 设计了MUCTA遗传算法. 该算法利用状态转移思想, 引进SDR算子获得多种分配次序种群, 同时以单行变异算子修正UAV与目标对应关系, 并采用最优个体法和轮盘赌法筛选子代个体.
%本实验目的是验证改进的DE离散目标分配算法的有效性
%实验设置:各种环境,调用目标分配的算法
%目标分配实验的输入:代价矩阵
%利用代价矩阵和映射方法,在离散和连续空间转换
%目标分配实验的输出:有效的基因染色体表示
%比较实验:
%1、可行性分析,三种模型
%2、进化策略对比分析,证明采用双策略的有效性
%3、大数据分析
%4、与其他方法的比较
% 本文只用到了AssignType =2;情形,即UAV数量大于TARGET数量
%使用了改动的遗传算法
%相比较源程序,较大改动部分为:对象执行区(GetFit1和Getfit2两个函数),和差分进化区(全部改动),其他部分有少量改动,我不记得了。很多部分直接删改,可能注释没有对应的上,强烈建议对比源代码学习观看
%本人编程能力较差,编写格式不规范,很多地方注释不足以及随心所欲各种直接删改,不同实验直接改数据,以及出现的重复,各种FOR循环嵌套等等,我自己都觉得乱七八糟。再次强烈建议对比源代码
%建议只使用该代码框架(即阅读源代码即可,本代码可适当看一下就行,估计很费劲),自行删改其中内容,写自己的文章,但注意源代码自行备份,自己的代码尽量多注释以及写实验说明,方便后来的师弟或师妹。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%清空环境
clear;
%定义地形对象
cTerrain = CTerrain3D;
%定义威胁区对象
cTread = CTread;
%调整为统一的图形环境
figure('Renderer','opengl');
%绘制地形和威胁区
cTerrain.draw();
cTread.draw();
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%数据形式说明
%xs 初始点位置集合,三维点集
%yt 目标点位置集合,三维点集
%MxsEna 能力矩阵,集合中的二元组表示最大最小飞行速度
%MxsDIs 最大航程矩阵,集合中的值表示UAV最大可飞的距离
%MytTOrd 任务点间的时序坐标,要求尽量在前面的先执行
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%调用目标分配算法
%AssignType表示不同的模型,1, N=M; 2, N>M; 3, N<M
%Key表示算法执行次数, 0,执行一次,1,执行多次
AssignType =2;
Key =0;
%时间测试
Time = cputime;
%% 第一种情况的实验
if AssignType == 1
%%%%%%%%%%%%%%%%%%%%%%%数据区%%%%%%%%%%%%
xs = [%11 2 3;2 17 5; 34 26 7;5 2 2;6 33 3;27 34 6;21 45 5;25 12 3;22 17 11;13 31 12;
%45 21 11; 36 22 11;13 21 16;41 25 10;25 25 11;53 12 14;22 12 12;18 32 11; 67 34 12;26 16 15;
78 20 15;93 31 12;31 20 13;112 32 15; 134 26 17;45 52 12;36 63 13;67 34 16;21 85 15;32 62 13;];
yt = [%40 210 12;170 90 13 ; 80 197 21 ;172 120 13;160 56 13;160 143 21;170 200 21;113 200 12;97 134 16;100 145 11;
%81 101 21; 72 152 12; 133 60 11;84 164 21; 150 90 21;146 121 12; 167 54 12; 108 165 12;99 120 21;110 143 11;
70 181 12;15 133 13 ; 19 151 12 ;160 192 13;101 120 23;160 113 12;82 101 11;173 140 12;182 65 14; 128 156 12;];
MxsEna=[%0.2 0.3; 0.2 0.4;0.4 0.75;0.3 0.6;0.2 0.3;0.35 0.45;0.3 0.5;0.3 0.6;0.2 0.3; 0.2 0.4;
% 0.4 0.75;0.3 0.6;0.2 0.3;0.35 0.45;0.3 0.5;0.3 0.6;0.2 0.3;0.35 0.45;0.3 0.5;0.3 0.6;
0.2 0.3; 0.2 0.4;0.4 0.75;0.3 0.6;0.2 0.3;0.35 0.45;0.3 0.5;0.3 0.6;0.3 0.5;0.3 0.6;];
MxsDis=[%400 700 650 500 700 900 450 610 400 700
%650 500 700 900 450 610 700 900 450 610
500 700 300 350 700 900 450 610 450 610];
ytW = [%1 3 4 2 1 1 3 2 1 2
%3 2 1 3 2 1 2 3 2 1
1 1 1 1 1 1 1 1 1 1];
MytTOrd=[3 4; 5 2; 6 8; 7 4;];
%引入新的协同矩阵,最大起始时间矩阵
Twait = [];
Twindow=[];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
if Key == 0
%%%%%%%%%%%%%%%%%%%%%%算法执行区%%%%%%%%%%%%%%%%%%
%调用目标分配算法,并取得解和相关数据,计算算法耗费时间
%定义目标分配算法对象
DDE1 = DMDEAssignTarget(cTerrain,xs,yt,MxsEna,MxsDis,ytW,MytTOrd,Twait,Twindow,1);
% MC = Cal1.GetMcost();
%Cal1 = CallocationTargetOld1(cTerrain);
%标签显示文字
xlabel('X/km')
ylabel('Y/km')
zlabel('Z/km')
%DDEAssign1=DDEAssignTarget1(cTerrain,xs,yt,MxsEna,MxsDis,ytW,MytTOrd);
%执行run并返回结果集
t1 = cputime;
[solU solT solC solF ] = DDE1.run();
Time = cputime -t1;
% %结果
solU
solT
solC
solF
Time
else if Key == 1
for i=1:10
DDE1 = DMDEAssignTarget(cTerrain,xs,yt,MxsEna,MxsDis,ytW,MytTOrd,Twait,Twindow,i);
% MC = Cal1.GetMcost();
%Cal1 = CallocationTargetOld1(cTerrain);
%标签显示文字
xlabel('X/km')
ylabel('Y/km')
zlabel('Z/km')
%DDEAssign1=DDEAssignTarget1(cTerrain,xs,yt,MxsEna,MxsDis,ytW,MytTOrd);
%执行run并返回结果集
t1 = cputime;
[solU solT solC solF ] = DDE1.run();
solu(i,:) = solU;
solt(i,:) = solT;
solc(i,:) = solC;
solf(i,:) = solF;
Time(i,:) = cputime -t1;
end %i
% %结果
solu
solt
solc
solf
Time
end % key=1
end % key=0
else if AssignType == 2
%% 第二种实验的情况
%%%%%%%%%%%%%%%%%%%%%%%数据区%%%%%%%%%%%%
xs = [%11 2 3;2 17 5; 34 26 7;5 2 2;6 33 3;27 34 6;21 45 5;25 12 3;22 17 11;13 31 12;
%45 21 11; 36 22 11;13 21 16;41 25 10;25 25 11;53 12 14;22 12 12;18 32 11; 67 34 12;26 16 15;
78 40 15;93 31 12;31 25 13;112 32 15; 134 26 17;45 52 12;36 55 13;67 34 16;21 45 15;160 30 13;];
yt = [%40 210 12;170 90 13 ; 80 197 21 ;172 120 13;160 56 13;160 143 21;170 200 21;113 200 12;97 134 16;100 145 11;
%81 101 21; 72 152 12; 133 60 11;84 164 21; 150 90 21;146 121 12; 167 54 12; 108 165 12;99 120 21;110 143 11;
70 151 12;40 155 13 ; 19 151 12 ;150 140 13 ];
MxsEna=[%0.2 0.3; 0.2 0.4;0.4 0.75;0.3 0.6;0.2 0.3;0.35 0.45;0.3 0.5;0.3 0.6;0.2 0.3; 0.2 0.4;
% 0.4 0.75;0.3 0.6;0.2 0.3;0.35 0.45;0.3 0.5;0.3 0.6;0.2 0.3;0.35 0.45;0.3 0.5;0.3 0.6;
0.2 0.3; 0.2 0.4;0.4 0.75;0.3 0.6;0.2 0.3;0.35 0.45;0.3 0.5;0.3 0.6;0.3 0.5;0.3 0.6;];
MxsDis=[%400 700 650 500 700 900 450 610 400 700
%650 500 700 900 450 610 700 900 450 610
500 700 300 350 700 900 450 610 450 610];
ytW = [%1 3 4 2 1 1 3 2 1 2
%3 2 1 3 2 1 2 3 2 1
1 1 1 1];
%这个数据里都代表的是目标点,是目标点与目标点的关系
MytTOrd=[3 2];
%引入新的协同矩阵,最大起始时间矩阵
Twait = [30 40 20 15 50 70 30 80 90 65];
Twindow=[];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
if Key == 0
%%%%%%%%%%%%%%%%%%%%%%算法执行区%%%%%%%%%%%%%%%%%%
%调用目标分配算法,并取得解和相关数据,计算算法耗费时间
%定义目标分配算法对象
DDE1 = DMDEAssignTarget(cTerrain,xs,yt,MxsEna,MxsDis,ytW,MytTOrd,Twait,Twindow,1);
% MC = Cal1.GetMcost();
%Cal1 = CallocationTargetOld1(cTerrain);
%标签显示文字
xlabel('X/km')
ylabel('Y/km')
zlabel('Z/km')
%DDEAssign1=DDEAssignTarget1(cTerrain,xs,yt,MxsEna,MxsDis,ytW,MytTOrd);
%执行run并返回结果集
[solU solT solC solF cpop ] = DDE1.run();
Time
cpop;
% %结果
solU
solT
solC
solF
Time
else if Key == 1
Time2=0;
cpop3=0;
for i=1:20
DDE1 = DMDEAssignTarget(cTerrain,xs,yt,MxsEna,MxsDis,ytW,MytTOrd,Twait,Twindow,i);
% MC = Cal1.GetMcost();
%Cal1 = CallocationTargetOld1(cTerrain);
%标签显示文字
xlabel('X/km')
ylabel('Y/km')
zlabel('Z/km')
%DDEAssign1=DDEAssignTarget1(cTerrain,xs,yt,MxsEna,MxsDis,ytW,MytTOrd);
%执行run并返回结果集
t1 = cputime;
[solU solT solC solF cpop ] = DDE1.run();
solu(i,:) = solU;
solt(i,:) = solT;
solc(i,:) = solC;
solf(i,:) = solF;
Time(i,:) = cputime -t1;
% genX(i,:)=cpop(:,2);
cpop2(:,i)=cpop(:,2);
Time(i)
end %i
% %结果
% figure(3);
% grid on;
% hold on;
% plot(genX(1:length(genX),1)',genX(1:length(genX),2)','linewidth',2);
% solu
% solt
% solc
% solf
Time=Time2/20;
cpop=cpop2/20;
end % key=1
end % key=0
else if AssignType == 3
%% 第三种实验的情况
%%%%%%%%%%%%%%%%%%%%%%%数据区%%%%%%%%%%%%
xs = [%11 2 3;2 17 5; 34 26 7;5 2 2;6 33 3;27 34 6;21 45 5;25 12 3;22 17 11;13 31 12;
%45 21 11; 36 22 11;13 21 16;41 25 10;25 25 11;53 12 14;22 12 12;18 32 11; 67 34 12;26 16 15;
78 20 15;93 31 12;31 20 13;112 32 15];
yt = [%40 210 12;170 90 13 ; 80 197 21 ;172 120 13;160 56 13;160 143 21;170 200 21;113 200 12;97 134 16;100 145 11;
%81 101 21; 72 152 12; 133 60 11;84 164 21; 150 90 21;146 121 12; 167 54 12; 108 165 12;99 120 21;110 143 11;
70 131 12;15 125 13 ; 19 151 12 ;142 120 13;120 100 23;160 90 12;82 101 11;173 140 12;160 160 14; 45 155 12;];
MxsEna=[%0.2 0.3; 0.2 0.4;0.4 0.75;0.3 0.6;0.2 0.3;0.35 0.45;0.3 0.5;0.3 0.6;0.2 0.3; 0.2 0.4;
% 0.4 0.75;0.3 0.6;0.2 0.3;0.35 0.45;0.3 0.5;0.3 0.6;0.2 0.3;0.35 0.45;0.3 0.5;0.3 0.6;
0.2 0.5; 0.3 0.4;0.4 0.75;0.3 0.45];
MxsDis=[%400 700 650 500 700 900 450 610 400 700
%650 500 700 900 450 610 700 900 450 610
700 700 900 650];
ytW = [%1 3 4 2 1 1 3 2 1 2
%3 2 1 3 2 1 2 3 2 1
1 1 1 1 1 1 1 1 1 1];
MytTOrd=[3 4; 5 2];
%引入新的协同矩阵,最大起始时间矩阵
Twait = [30 40 20 15];
Twindow=[1300,6000];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
if Key == 0
%%%%%%%%%%%%%%%%%%%%%%算法执行区%%%%%%%%%%%%%%%%%%
%调用目标分配算法,并取得解和相关数据,计算算法耗费时间
%定义目标分配算法对象
DDE1 = DMDEAssignTarget(cTerrain,xs,yt,MxsEna,MxsDis,ytW,MytTOrd,Twait,Twindow,1);
% MC = Cal1.GetMcost();
%Cal1 = CallocationTargetOld1(cTerrain);
%标签显示文字
xlabel('X/km')
ylabel('Y/km')
zlabel('Z/km')
%DDEAssign1=DDEAssignTarget1(cTerrain,xs,yt,MxsEna,MxsDis,ytW,MytTOrd);
%执行run并返回结果集
t1 = cputime;
[solU solT solC solF] = DDE1.run();
Time = cputime -t1;
% %结果
solU
solT
solC
solF
Time
else if Key == 1
for i=1:20
DDE1 = DMDEAssignTarget(cTerrain,xs,yt,MxsEna,MxsDis,ytW,MytTOrd,Twait,Twindow,i);
% MC = Cal1.GetMcost();
%Cal1 = CallocationTargetOld1(cTerrain);
%标签显示文字
xlabel('X/km')
ylabel('Y/km')
zlabel('Z/km')
%DDEAssign1=DDEAssignTarget1(cTerrain,xs,yt,MxsEna,MxsDis,ytW,MytTOrd);
%执行run并返回结果集
t1 = cputime;
[solU solT solC solF ] = DDE1.run();
solu(i,:) = solU;
solt(i,:) = solT;
solc(i,:) = solC;
solf(i,:) = solF;
Time(i,:) = cputime -t1;
end %i
% %结果
solu
solt
solc
solf
Time
end % key=1
end % key=0
end % type =3
end % type =2
end % type=1
完整代码或者仿真咨询添加QQ1575304183
以上是关于POE 利用区块链挖掘协同执行遗传算法的主要内容,如果未能解决你的问题,请参考以下文章