斐波那契数列有啥规律

Posted 2023-04-09

参考技术A F(n)=F(n-1)+F(n-2) 参考技术B 斐波拉契数列的简介
　　斐波拉契数列（又译作“斐波那契数列”或“斐波那切数列”）是一个非常美丽、和谐的数列，它的形状可以用排成螺旋状的一系列正方形来说明（如右词条图），起始的正方形(图中用灰色表示)的边长为1，在它左边的那个正方形的边长也是1 ，在这两个正方形的上方再放一个正方形，其边长为2，以后顺次加上边长为3、5、8、13、2l……等等的正方形。这些数字每一个都等于前面两个数之和，它们正好构成了斐波那契数列。“斐波那契数列”的发明者，是意大利数学家列昂纳多·斐波那契（Leonardo Fibonacci，生于公元1170年，卒于1240年。籍贯大概是比萨）。他被人称作“比萨的列昂纳多”。1202年，他撰写了《珠算原理》(Liber Abaci)一书。他是第一个研究了印度和阿拉伯数学理论的欧洲人。他的父亲被比萨的一家商业团体聘任为外交领事，派驻地点相当于今日的阿尔及利亚地区，列昂纳多因此得以在一个阿拉伯老师的指导下研究数学。他还曾在埃及、叙利亚、希腊、西西里和普罗旺斯研究数学。

　　斐波那契数列指的是这样一个数列：1，1，2，3，5，8，13，21，34……
　　这个数列从第三项开始，每一项都等于前两项之和。它的通项公式为：(1/√5)*[(1+√5)/2]^n - [(1-√5)/2]^n　(√5表示5的算术平方根)　(19世纪法国数学家敏聂(Jacques Phillipe Marie Binet 1786-1856)
很有趣的是：这样一个完全是自然数的数列，通项公式居然是用无理数来表达的。
斐波拉契数列的出现
　　13世纪初，欧洲最好的数学家是斐波拉契；他写了一本叫做《算盘书》的著作，是当时欧洲最好的数学书。书中有许多有趣的数学题，其中最有趣的是下面这个题目：
　　“如果一对兔子每月能生1对小兔子，而每对小兔在它出生后的第3个月裏，又能开始生1对小兔子，假定在不发生死亡的情况下，由1对初生的兔子开始，1年后能繁殖成多少对兔子？”
斐波拉契把推算得到的头几个数摆成一串：1，1，2，3，5，8……
　　这串数里隐含着一个规律：从第3个数起，后面的每个数都是它前面那两个数的和。而根据这个规律，只要作一些简单的加法，就能推算出以后各个月兔子的数目了。
　　于是，按照这个规律推算出来的数，构成了数学史上一个有名的数列。大家都叫它“斐波拉契数列”，又称“兔子数列”。这个数列有许多奇特的的性质，例如，从第3个数起，每个数与它后面那个数的比值，都很接近于0.618，正好与大名鼎鼎的“黄金分割律”相吻合。人们还发现，连一些生物的生长规律，在某种假定下也可由这个数列来刻画呢。
　　斐氏本人对这个数列并没有再做进一步的探讨。直到十九世纪初才有人详加研究，1960年左右，许多数学家对斐波拉契数列和有关的现象非常感到兴趣，不但成立了斐氏学会，还创办了相关刊物，其后各种相关文章也像斐氏的兔子一样迅速地增加。
斐波拉契数列的来源及关系
斐波拉契（Fibonacci）数列来源于兔子问题，它有一个递推关系，
f(1)=1
f(2)=1
f(n)=f(n-1)+f(n-2),其中n>=2
f(n)即为斐波拉契数列。
斐波拉契数列的公式
它的通项公式为:[（1＋√5）/2]^n － [（1－√5）/2]^n /√5 （注：√5表示根号5）
斐波拉契数列的某些性质
1)，f(n)f(n)-f(n+1)f(n-1)=(-1)^n;
2), f(1)+f(2)+f(3)+……+f(n)=f(n+2)-1
3),arctan[1/f(2n+1)]=arctan[1/f(2n+2)]+arctan[1/f(2n+3)]

斐波那契查找算法解析

文章目录

• 前言
• 一、斐波那契数列
• 二、斐波那契查找算法

---

前言

学数据结构的时候被斐波那契查找算法困扰，刚开始难以理解，脑袋有点懵，翻看了许多大佬的博文，加上自己的理解发了出来

一、斐波那契数列

我们先看什么是斐波那契数列
有这样一个数列：1,1,2,3,5,8,13,21…
我们可以尝试找一下规律，并将后面的数字都按照这种规律在数列中呈现
我们发现从第3个数字开始，每个数字等于前两个数字之和
所以第n个数字
f(n) = f(n-1)+f(n-2)
符合这样规律的数列我们称之为斐波那契数列

二、斐波那契查找算法

斐波那契查找算法原理和二分插值查找算法一样，在于寻找分割点，依据分割点将数组进行分割，判断分割点处数字大小和要找的数字大小的关系进行递归处理，我们所要找的mid位于黄金分割点附近即mid=low+F(k-1)-1,F代表斐波那契数列，如下图所示

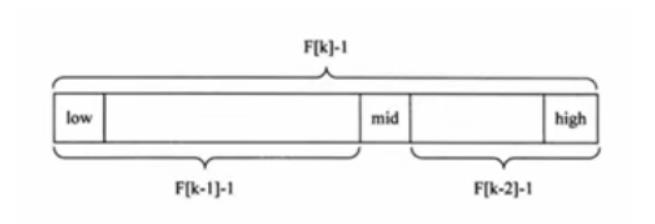
我们举个例子，有数组arr = {1,8,10,89,1000,1234};，我们需要找到1234在数组中的下标
第一步
在斐波那契数列找一个等于略大于查找数组中元素个数的数F[n]，数组中元素个数为6，我们创建一个斐波那契数列出来我们定义为f[k]，f={1 1 2 3 5 8 13}（我们默认长度为7），我们要找的分割点的值就为8,因为它的数值略大于数组的元素个数。
第二步
我们找到的分隔值的大小为我们需要的数组的大小，如果大于数组长度，我们就需要创建一个新的数组，将老数组arr的值分别赋值给新数组temp，int[] temp = Arrays.copyOf(arr,f[k]);并且因为temp的长度大于arr所以arr.length之后的数组元素为0，我们需要用arr数组的最后一个元素对其进行填充
第三步
接下来就是查找中间值，根据公式f(n) = f(n-1)+f(n-2),我们新数组长度为8，则f[6]=f[5]+f[4],即8=5+3,则中间值为mid=5，得到中间值我们就进行判断递归，如果temp[mid]>value则左递归，反之向右递归

代码奉上

package org.wql.Chazhao;

import java.util.Arrays;

/**斐波那契查找
 * Description
 * User:
 * Date:
 * Time:
 */
public class FeiboNaqi {
    public static int maxSize = 20;
    public static void main(String[] args) {
        int[] arr = {1,8,10,89,1000,1234};
        int index = feibonaqi(arr, 1234);
        System.out.println(index);
    }

    //斐波那契查找算法
    private static int feibonaqi(int[] arr, int key) {
        int low = 0;
        int high = arr.length-1;//代表原数组最高的下标4
        int k = 0;//斐波那契分割数值的下标
        int mid;
        int[] f = fib();
        //获取到斐波那契分割数值的下标 1 1 2 3 5 8
        while (arr.length > f[k]-1){//6 2
            k++;//4
        }
        //因为f[k]值可能大于a的长度，因此我们需要使用Arrays类，构造一个新的数组，并指向a[]
        int[] temp = Arrays.copyOf(arr,f[k]);
        //填充新的数组，因为新数组长度如果比原数组大，多的部分会被填充0
        for(int i = high+1;i<temp.length;i++){
            temp[i] = arr[high];
        }
        //找到中间值mid后开始查找
        while (low <= high){//只要这个条件满足，就可以继续查找
            mid = low+f[k-1]-1;
            if(key<temp[mid]){//向左查找
                high = mid-1;
                //为什么是k--
                //说明
                //1.全部元素 = 前面的元素 + 后边元素
                //2.f[k] = f[k-1]+f[k-2]
                //因为前面有f[k-1]个元素，所以可以继续拆分f[k-1] = f[k-2] + f[k-3]
                //即在f[k-1]的前面继续查找k--
                //即下次循环mid = f[k-1-1]-1
                k--;
            }else if(key>temp[mid]){
                low = mid+1;
                //为什么是k-=2
                //说明
                //继续拆分f[k-2] = f[k-3] + f[k-4]
                //即在f[k-2]的前面继续查找k-=2
                //即下次循环mid = f[k-1-1-1]-1
                k-=2;
            }else {
                if(mid<=high){
                    return mid;
                }else {
                    //数组扩容过，此时返回mid就会超出原数组的长度
                    return high;
                }
            }
        }
        return -1;
    }

    //因为后面我们mid=low+F(k-1)-1,需要使用到斐波那契数列，因此我们需要先获取到一个斐波那契数列
    //非递归方法得到一个斐波那契数列
    public static int[] fib(){
        int[] f = new int[maxSize];
        f[0] = 1;
        f[1] = 1;
        for (int i=2;i<maxSize;i++){
            f[i] = f[i-1] + f [i-2];
        }
        return f;
    }
}

我们查找的value=1234