opencv相机标定和人头姿态估计案例

Posted 2022-11-09 风翼冰舟

前言

头部驱动除了之前关注的表情驱动外，还有眼球驱动和头部方向驱动。本博客基于opencv官方文档和部分开源代码来研究如何基于人脸关键点获取头部的朝向。

国际惯例，参考博客：

opencv:Camera Calibration and 3D Reconstruction

opencv:Real Time pose estimation of a textured object

cv.solvePnP位姿估计旋转向量精度分析

头部姿态估计原理及可视化

重磅！头部姿态估计「原理详解 + 实战代码」来啦！

相机矩阵(Camera Matrix)

Python cv2.decomposeProjectionMatrix方法代码示例

face_landmark

head-pose-estimation

Face-Yaw-Roll-Pitch-from-Pose-Estimation-using-OpenCV

talking-head-anime-demo

OpenVtuber

相机标定理论

几种坐标系

先看从opencv官网中扒下来的两幅图，代表针孔相机模型(pinhole camera model)

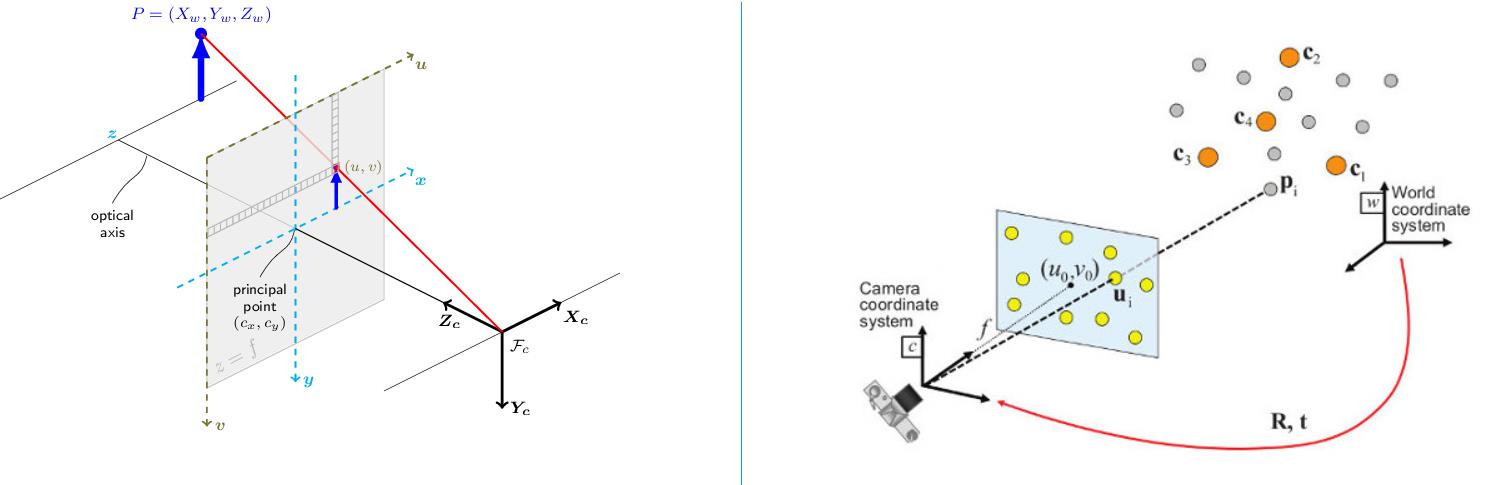
其中涉及到几种坐标系：

• 世界坐标系：一个固定不变的坐标系，原点通常固定不变，右图的$w$坐标系
• 相机坐标系：相机在世界坐标系下的姿态，右图的$c$坐标系
• 图像坐标系：成像平面，图中的x-y坐标轴，其原点是相机的光轴与成像平面的胶垫
• 像素坐标系：最终图像，图中的u-v坐标轴，原点在左上角，就跟opencv输出的图片一样，左上角代表$(0,0)$像素位置。

图像坐标系和像素坐标系横轴和纵轴方向一致，但是单位不同，一个是物理单位，一个是像素单位，一般有一个对应的缩放关系，代表一个像素在成像平面上的大小。

针孔相机的目标就是把3D坐标点$P_w$利用透视变换(perspective transformation)投影到图像平面上，得到对应像素$p$。其中$P_w$和$p$都在齐次坐标系下表示。

无畸变情况下，针孔相机的投影变换可以表示为：
$$sp=A[R|t]P_w$$
其中$P_w$为世界坐标系下的3D坐标点，$p$是图像平面上的2D像素点，$A$是相机内参矩阵，$R$和$t$分别描述了世界坐标系到相机坐标系的旋转和平移变换，$s$是任意尺度的投影变换(非相机模型的参数，其实就是图像坐标系到像素坐标系的变换系数)。

世界坐标系到相机坐标系

旋转-平移矩阵$[R|t]$是投影变换(projective transformation)和齐次变换(homogeneous transformation)的乘积。

维度为$(3,4)$投影变换可以将相机坐标系里的3D坐标映射到成像平面的2D坐标，并且在归一化的相机坐标系$x^{\prime }=\frac{X_c}{Z_c}$和$y^{\prime }=\frac{Y_c}{Z_c}$下表示出来
$$Z_c\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\\ 1\end{array}\right]$$
而齐次变换通常在相机外参$R$和$t$中体现出来，代表世界坐标系到相机坐标系的变换，因此给定一个世界坐标系下的点$P_w$，那么相机坐标系下的对应点为:
$$P_c=\left[\begin{array}{cc}R& t\\ 0& 1\end{array}\right]P_w$$
这个齐次变换一般就是由一个(3,3)的旋转矩阵和一个(3,1)的平移向量组成：
$$\left[\begin{array}{cc}R& t\\ 0& 1\end{array}\right]=\left[\begin{array}{cccc}{r}_{11}& r_{12}& r_{13}& t_x\\ r_{21}& r_{22}& r_{23}& t_y\\ r_{31}& r_{32}& r_{33}& t_z\\ 0& 0& 0& 1\end{array}\right]$$
因此
[ X c Y c Z c 1 ] = [ r 11 r 12 r 13 t x