湖南省第十届大学生计算机程序设计竞赛（HNCPC2014）CSG - 1123 : 点到圆弧的距离（计算几何）

Posted 2022-11-05 quinn18

文章目录

• • 题意
  • 题解
  • 代码
• 总结

题目链接

---

题意

：输入一个点 $P$ 和一条圆弧（圆周的一部分），你的任务是计算 $P$ 到圆弧的最短距离。换句话说，你需要在圆弧上找一个点，到 $P$ 点的距离最小。

题解

：呃
先找圆心
显然
假如点跟圆心的连线在那段扇形的圆弧范围内，点到圆弧的最短距离为点到圆心的距离减去半径然后取绝对值；不然，点到圆弧的最短的距离为到这段圆弧的两个端点的最小值。

那怎么判断是不是在圆弧范围内呢？

本来想找PB和OA,OC是否有交点但是wa了好像不是精度问题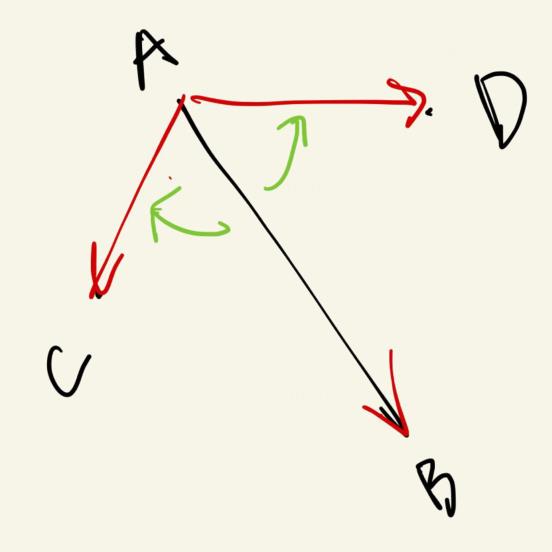
两个点是不是在一条线的两端可以用叉积判断
判断 $C,D$ 点是否在$AB$线段两边
向量$AB$和向量$AC$是顺时针，所以他们的叉积 $>0$
向量$AB$和向量$AD$是逆时针，所以他们的叉积 $<0$
只要$Cross(AB,AC)\ast Cross(AB,AD)<0$时，就是在不在同一侧
所以这样看，$B$ 就在射线 $AC$ 和 $AD$ 中间~就可以判断$P$是否在圆环范围内
对于这题就可以用来判断 $P$是否在 $OC,OA$之间

但是上面只适用劣弧的情况 还要考虑平角和优弧的情况 反正还是用这个叉积判qaq

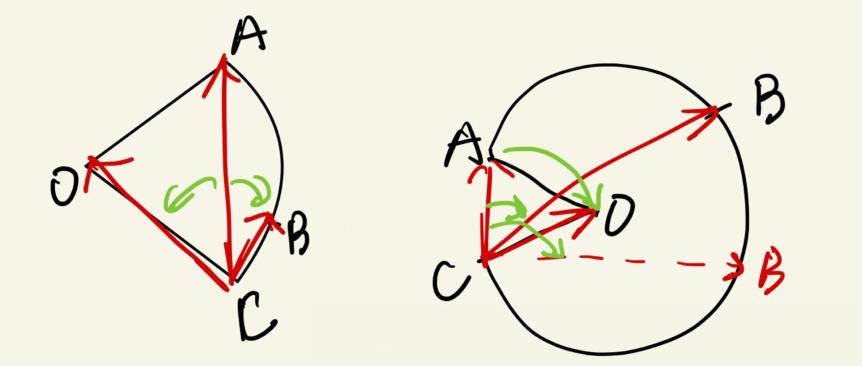
代码

：

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define int long long
const double eps = 1e-8;
const double PI = acos(-1.0);
int sgn(double x) 
    if (fabs(x) < eps) 
        return 0;
    
    return (x < 0) ? -1 : 1;

struct Point 
    double x, y;
    Point(double x = 0.0, double y = 0.0) : x(x), y(y) 
;
typedef Point Vector; //向量
Vector operator + (Vector A, Vector B)  //向量加法
    return Vector(A.x + B.x, A.y + B.y);

Vector operator - (Point A, Point B) 
    return Vector(A.x - B.x, A.y - B.y);

Vector operator * (Vector A, double p) 
    return Vector(A.x * p, A.y * p);

Vector operator / (Vector A, double p) 
    return Vector(A.x / p, A.y / p);

bool operator < (const Point A, const Point B) 
    return A.x < B.x || (sgn(A.x - B.x) == 0 && A.y < B.y);

bool operator == (const Point A, const Point B) 
    return sgn(A.x - B.x) == 0 && sgn(A.y - B.y) == 0;

double Dot(Vector A, Vector B) //点积
    return A.x * B.x + A.y * B.y;

double Cross(Vector A, Vector B) //向量叉积
    return A.x * B.y - A.y * B.x;

double Length(Vector A) //模
    return sqrt(Dot(A, A));

Vector Normal(Vector A) //单位向量
    double L = Length(A);
    return Vector(-A.y / L, A.x / L);

Point GetLineIntersection(Point P, Vector v, Point Q, Vector w) //两直线焦点
    Vector u = P - Q;
    double t = Cross(w, u) / Cross(v, w);
    return P + v * t;

double dis(Point a, Point b) 
    return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));

signed main() 
    int t=0;
    double x1, y1, x2, y2, x3, y3, xp, yp;
    while(cin >> x1 >>y1 >> x2 >> y2 >> x3 >> y3 >> xp >> yp) 

        Point A =  x1,y1 ;
        Point B =  x2,y2 ;
        Point AB =  (x1 + x2) / 2,(y1 + y2) / 2 ;
        Point C =  x3,y3 ;
        Point BC =  (x3 + x2) / 2,(y3 + y2) / 2 ;
        Point P =  xp,yp ;
        Point O = GetLineIntersection(AB, Normal(A - B), BC, Normal(B - C));//也可以用三角形外心找圆心

		double ans = min(dis(P, A), dis(P, C));
        double d = dis(O, P);
        double r = dis(O, A);
		if((2*r==dis(A, C))) 
			if(Cross(A-C, A-P)*Cross(A-C,A-B)>=0) 
				ans=min(ans, fabs(d-r));
			
			cout << "Case " << ++t << ": " <<fixed<< setprecision(3) << ans << endl;
			continue;
		
        if(Cross(C-A, C-B)*Cross(C-A, C-O)<0) 
			if(Cross(O-A, O-P)*Cross(O-A,O-C)>=0&&Cross(O-C, O-P)*Cross(O-C,O-A)>=0) 
				ans=min(ans, fabs(d-r));
			
        else 
			if(!(Cross(O-A, O-P)*Cross(O-A,O-C)>=0&&Cross(O-C, O-P)*Cross(O-C,O-A)>=0)) 
				ans=min(ans, fabs(d-r));
			
        
        cout << "Case " << ++t << ": " <<fixed<< setprecision(3) << ans << endl;
    
    return 0;

---

总结

一道计算几何 暖你一整天