简洁而优美的结构 - 并查集 | 一文吃透 “带权并查集” 不同应用场景 | “手撕” 蓝桥杯A组J题 - 推导部分和

Posted 2023-04-08 Dream-Y.ocean

💛前情提要💛

本章节是每日一算法的并查集&带权并查集的相关知识~

接下来我们即将进入一个全新的空间，对代码有一个全新的视角~

以下的内容一定会让你对数据结构与算法有一个颠覆性的认识哦！！！

❗以下内容以C++/java的方式实现，对于数据结构与算法来说最重要的是思想哦❗

以下内容干货满满，跟上步伐吧~

---

作者介绍：

🎓 作者： 热爱编程不起眼的小人物🐐
🔎作者的Gitee：代码仓库
📌系列文章&专栏推荐： 《刷题特辑》、 《C语言学习专栏》、《数据结构_初阶》 、《C++轻松学_深度剖析_由0至1》、《Linux - 感受系统美学》

📒我和大家一样都是初次踏入这个美妙的“元”宇宙🌏 希望在输出知识的同时，也能与大家共同进步、无限进步🌟
🌐这里为大家推荐一款很好用的刷题网站呀👉点击跳转

---

📌导航小助手📌

• 💡本章重点
• 🍞一.并查集
• • 🥐Ⅰ.朴素版并查集
  • 🥯Ⅱ.总结
• 🍞二.带权并查集
• • 🥐Ⅰ.维护size的并查集
  • 🥐Ⅱ.维护dist的并查集
  • 🥯Ⅲ.总结
• 🍞三.并查集综合模板
• 🍞四.蓝桥杯A组J题
• 🫓总结

---

💡本章重点

• 并查集的算法理解

• 带权并查集详解

• 并查集的实际应用：蓝桥杯A组J题 - 推导部分和

---

🍞一.并查集

💡并查集算法：

• 本质：并查集主要维护的是一个集合，主要作用于元素分组问题，即可以支持我们快速查询两个元素是否在同一个集合内的操作

• 因此，并查集支持在 $O(1)$ 的时间复杂度内执行以下两个操作：

  • 合并：将两个不相交的集合合并为一个集合

  • 查询：查询两个元素是否在同一集合内

• 思想：在逻辑结构上，每个集合都可以想象成用一棵树来表示，而树的根节点的编号就是整个集合的编号，即对于树中（集合内）的每一个节点存储的都是其父节点

❗特别注意：

• 上述所描述的思想是抽象成以树的逻辑结构所分析的

• 但在实际应用中，为了提高效率，真正使用的其实是数组形式的物理结构

• 而这也就解释了为什么可以以 $O(1)$ 的时间复杂度去查询了：

  • 正是因为数组拥有随机访问的特性，从而只要在数组中找到节点所对应的位置，并在此位置上存储其父亲节点，不断往上寻找直至寻找至根节点（即整个集合的编号）

  • 即可知此节点对应的元素从属于哪个集合，从而也就可以判断任两个元素是否在同一个集合中了

👉接下来就让我们深入分析并查集是如何实现的吧~

---

🥐Ⅰ.朴素版并查集

💡朴素版并查集：

• 此版本的并查集是最基础的

• 而其它版本的并查集也正是由此基础上添加并维护额外信息得出的

👉定义并查集&初始化：

存储每个节点的祖宗节点：
int p[N];

假定节点编号是1~n，并在初始化的时候指向自己：
for (int i = 1; i <= n; i ++ ) p[i] = i;

👆特别注意：

• 每个节点存储其父亲节点，我们采用的是p[x]：表示x的父节点为p[x]的值

• 【前提：假定节点的编号（即数组的下标）为1~n】也就是说，在初始化阶段的时候，每个节点的父亲节点都是自己，简单来说就是在初始化的时候自己是自成一个集合

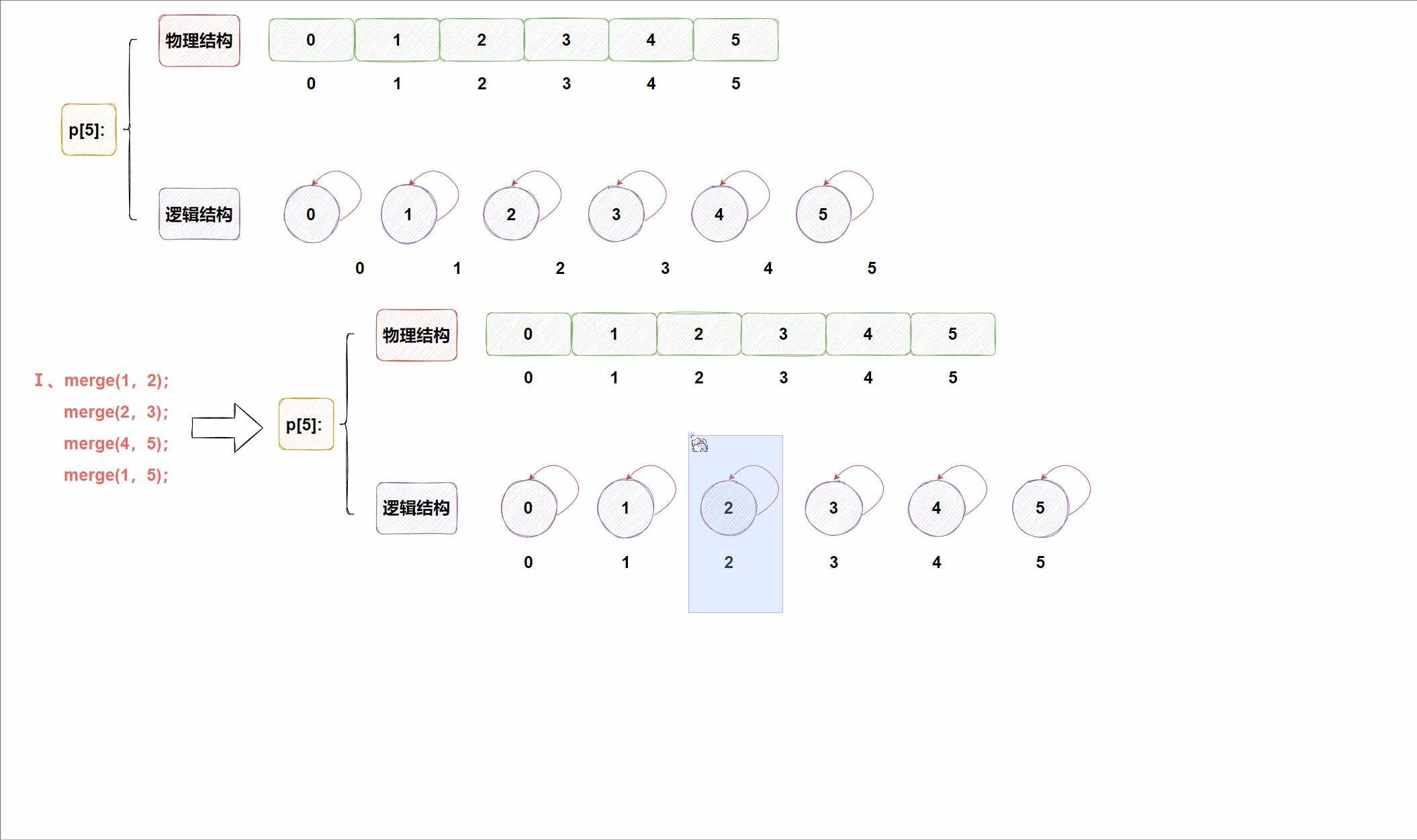
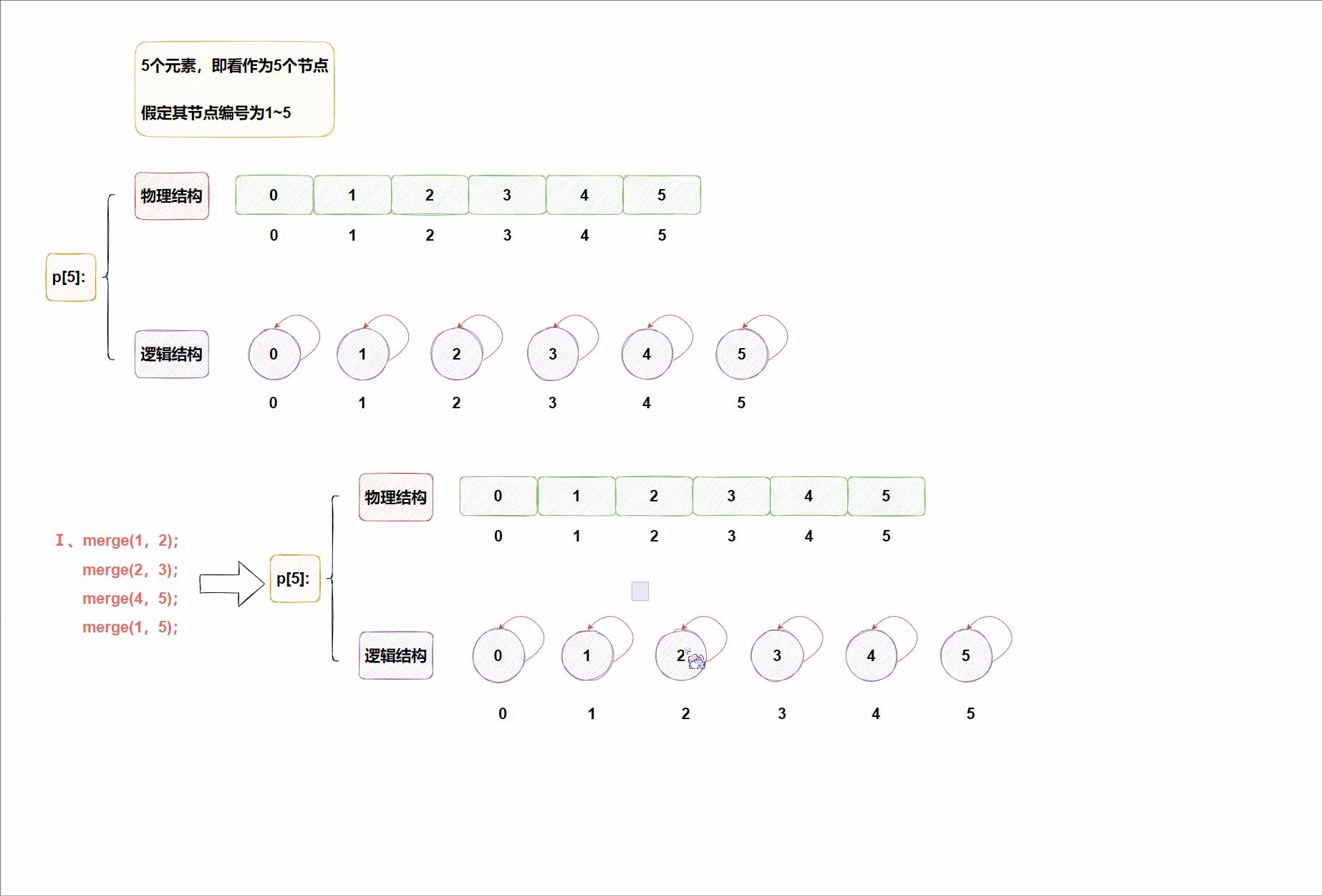
⭐示例：

• 假设目前需要对5个元素进行并查集的操作，而在操作前需要进行初始化

• 初始化后的结构如下：

❓由上述的并查集定义&初始化中，引发了三个问题：

• 🔴如何判断树根，也就是说如何判断已经找到此集合的根节点？

  • 答案：只要if(p[x] == x)，即可知此时已经找到此集合的根节点

• 🟠如何求x的集合编号，以及如何优化？

  • 答案：因为每个节点是存储的是父亲节点，由只要不断迭代，直至根节点为止，那么x元素属于的集合编号就是根节点的编号：while(p[x] != x) x = p[x];

  • 而当前每一次的查找方式的时间复杂度和树的高度次数有关，但我们可以优化为：在找某个节点的根节点的时候，我们可以顺带将此路径上的所有的点都直接指向根节点【即只需要查找一次，这路径上的点都可以一步到位直接指向根节点】

  • 也就是说，后续查找某个节点的根节点的时候，无需再由迭代的方式查找根节点了，而是此时的节点直接指向（存储）的就是根节点（集合编号），这个优化方式便叫作：路径压缩优化

  • 这样判断两个元素是否在同一集合内就更直接了

• 🟡如何合并两个集合？

  • 答案：px是x的集合编号，py是y的集合编号，令p[x] = y;即可

  • 即简单来说就是将x的祖宗变为y的祖宗的儿子【将x节点所在的集合的根节点（集合编号）指向y节点所在的集合的根节点（集合编号）】

👉解决了上述问题后，我们来具体实现并查集的两个操作吧~

---

1️⃣优化前的并查集操作：

• 查询操作：

int find(int x) 

    if (x == p[x]) return p[x];
	
	while(p[x] != x) x = p[x];
	
	return p[x];

• 合并操作：

bool merge(int x, int y) 

    x = find(x);
    y = find(y);

    if (x == y) return false;

    //将 y节点所在的集合 合并到 x节点的集合上
    //【即 将y节点的祖宗 变为 x节点的祖宗】
    p[y] = x;

    return true;

• 合并操作➕查询操作动图示例：

2️⃣优化后的并查集查询操作：

• 查询操作：

int find(int x)

    if (p[x] != x) p[x] = find(p[x]);
    
    return p[x];

👆路径压缩优化细节：

• 优化前的查询操作和优化后的查询操作的不同具体体现在：优化后的查询操作会将查询路径上的节点原本存储的是其父亲节点，而变为直接存储根节点

• 因为p[N]数组为全局数组，因此函数内对数组的修改会影响到原数组内的值，从而可以借助函数的递归和回溯操作对路径上的节点变为直接指向根节点的值，从而达到优化的效果

• 合并操作➕查询操作动图示例：

👉综上：朴素版并查集整体代码如下

1️⃣定义并查集&初始化：

int p[N];

for (int i = 1; i <= n; i ++ ) p[i] = i;

2️⃣并查集的查询操作：

int find(int x)

    if (p[x] != x) p[x] = find(p[x]);
    
    return p[x];

3️⃣并查集的合并操作：

bool merge(int x, int y) 

    x = find(x);
    y = find(y);

    if (x == y) return false;

    p[y] = x;

    return true;

---

🥯Ⅱ.总结

⭐综上：

• 以上就是朴素版的并查集的实现啦

• 并查集是被很多人公认的最简洁而优雅的数据结构之一，建议同学们反复阅读掌从而握它呀~

---

🍞二.带权并查集

💡带权并查集：

• 简单来说：带权并查集就是在朴素并查集的基础上，对朴素并查集中维护集合关系的树中添加边权，并对此维护，以达到维护更多信息的并查集

❓什么是权值：

• 对于带权并查集而言，权值代表着当前节点与父节点的某种关系（即使路径压缩了也是这样），我们便可以通过这两者的关系，将同一棵树下（同一个集合中）两个节点的关系也表示出来

• 而权值在这里一般有两种意思，也就说可以在朴素版的并查集的基础上多维护以下两种信息：

  • 1️⃣权值为size时：表示记录当前并查集集合内的节点个数，也称为维护size的并查集

  • 2️⃣权值为dist时：表示记录当前节点到到祖宗节点距离，也称：维护dist的并查集

👉有了以上对带权并查集的了解，接下来就让我们深入了解两种不同的带权并查集吧~

---

🥐Ⅰ.维护size的并查集

💡维护size的并查集：

• 简单来说：就是在朴素版的并查集的基础上维护多一个信息size，从而记录当前并查集集合内的节点个数

• 此并查集一般作用于计算连通块中点的数量的题目

👉代码实现：

1️⃣定义并查集&初始化：

int p[N], _size[N];

for (int i = 1; i <= n; i ++ )

    p[i] = i;
    
    size[i] = 1;

👆特别注意：

• p[]存储的是每个点的祖宗节点

• size[]只有祖宗节点的有意义，表示祖宗节点所在集合中的点的数量

2️⃣并查集的查询操作：

int find(int x)

    if (p[x] != x) p[x] = find(p[x]);
    
    return p[x];

3️⃣并查集的合并操作：

 bool merge(int x, int y) 

    x = find(x);
    y = find(y);

    if (x == y) return false;

    _size[x] += _size[y];
    
    p[y] = x;

    return true;

👆特别注意：

• 因为是合并集合，固然也需要将原来集合内的节点总个数加到新合并的集合中

🌰举个例子：

---

🥐Ⅱ.维护dist的并查集

💡维护dist的并查集：

• 简单来说：就是在朴素版的并查集的基础上维护多一个信息dist，从而记录当前节点到根节点之间的距离

• 此并查集一般作用于如：食物链等题目

👉代码实现：

1️⃣定义并查集&初始化：

int p[N], _dist[N];

for (int i = 1; i <= n; i ++ )

     p[i] = i;
     
     _dist[i] = 0;

👆特别注意：

• p[]存储的是每个点的祖宗节点

• d[x]存储的是编号为x的节点到p[x]（祖宗节点）的距离

2️⃣并查集的查询操作：

int find(int x)

    if (p[x] != x)
    
        int root = find(p[x]);
        
        _dist[x] += _dist[p[x]];
        
        p[x] = root;
    
    
    return p[x];

⭐以上操作的细节：

• 我们需要注意的是，在 路径压缩的过程中，我们需要顺带计算此节点距离祖宗节点的距离，此时我们便需要提前记录每一次递归（即寻找到父亲节点）前的节点的编号

• 即记录下当前所操作的节点编号，这样就能在递归回溯的时候，对记录下的节点进行距离根节点的距离的更新

• 从而可以达到借助路径压缩的优化达到不仅仅是对路径节点的优化，也达到了对dist的优化，即一次查询即可更新路径上所有的点到根节点的距离

3️⃣并查集的合并操作：

bool merge(int x, int y) 

    x = find(x);
    y = find(y);

    if (x == y) return false;

    _dist[y] += _dist[x] + 1;

    p[y] = x;

    return true;

❓上述实现中，可能会有如下疑惑：

• 为什么y集合合并到x集合，只需要更新y集合的根节点距离新集合根节点的距离，而不需要将y集合内的所有节点距离新根节点的距离全部更新呢？

• 这是因为：只要后续操作中，需要对原y集合内的某个节点进行查询操作的时候，查询操作便会对此点所在路径上的所有点全部进行数据的更新，即相当于原y集合内的节点的p[x]和_dist[x]都会更新为指向合并后新的根节点和距离新根节点的距离

• 也就是说，只要合并的时候更新好原根节点距离新根节点的距离，后续只需要一次查询操作，便可将数据都更新为最新的了

🌰举个例子：

---

🥯Ⅲ.总结

⭐综上：

• 以上就是带权并查集的全部内容了：

  • 若权值体现在集合上，一般开一个size数组来统计集合的大小

  • 若权值体现在边上，可表示当前节点到父节点的距离等意思

• 而具体需要使用哪种并查集，维护哪些信息，就需要视具体题意来决定

• 但是，如果遇到需要同时维护size 和dist的情况，我们该怎么办呢？

👉而以下所提及的方法就可以很好解决上述问题啦~

---

🍞三.并查集综合模板

💡并查集综合模板：

• 在遇到上述所提及的情况的时候，我们再创建现场合并两个并查集就略显麻烦了

• 于是，我们便可以提前将带权并查集将其整合起来，变成一个类（算法模板），对并查集的操作变为类的方法（即成员函数）

• 这样在遇到相应题目的时候，就可以直接调用此类生成一个对象，再调用相应的成员函数去解决啦

• 而且维护成模板的好处是：在做题量丰富的情况下，可以将经常用到的方法（Eg：判等、求距离……）整合为成员方法，这样就可以有助于我们快速解决题目啦

👉带权并查集算法模板：

//三合一的并查集模板：
//1、朴素版的并查集
//2、维护size【即维护集合中点的数量】
//3、维护集合内的节点到根节点的距离
struct UF 

    std::vector<int> p, _dist, _size;

    UF(int n) 
    : p(n)        //存储每个点的祖宗节点
    , _dist(n, 0) //维护当前到祖宗节点距离的数组
    , _size(n, 1) //维护当前的集合中的点的个数的数组（1是因为已经有自己了）
     
        //初始化并查集
        //假定节点编号为：1~n
        for(int i = 1; i <= n; i++) p[i] = i;
    
    
    //路径压缩优化
    //顺带维护距离
    int find(int x) 
    
        if (x == p[x]) return p[x];

        //先记录祖宗
        int root = find(p[x]);

        //加上父亲的距离
        _dist[x] += _dist[p[x]];

        //指向祖宗
        return p[x] = root;
    

    //判断祖宗节点是否为同一个
    //即 判断是否为同一个祖宗
    bool same(int x, int y) 
     
        return find(x) == find(y); 
    

    //合并并查集
    bool merge(int x, int y) 
    
        x = find(x);
        y = find(y);

        if (x == y) return false;

        //本来d[y]（即 祖宗节点 到 祖宗节点的距离）等于0
        //现在它指向新祖宗的距离 就是 合并到新集合中 的 新集合中的元素个数
        _dist[y] += _size[x];

        _size[x] += _size[y];

        //将 y节点所在的集合 合并到 x节点的集合上
        //【即 将y节点的祖宗 变为 x节点的祖宗】
        p[y] = x;

        return true;
    

    //表示祖宗节点所在集合中的点的数量
    int size(int x) 
     
        return _size[find(x)]; 
    

    //查询两点之间相差几个人，不在一列返回-1
    int dist(int x, int y) 
    
        if (!same(x, y)) return -1;

        return abs(p[x] - p[y]) - 1;
    
;

➡️接下来就让我们来道题目实践一下吧~

---

🍞四.蓝桥杯A组J题

🔍题目传送门：推导部分和

对于一个长度为 $N$ 的整数数列 $A_1,A_2,\dots A_N$，小蓝想知道下标 $l$ 到 $r$ 的部分和 ${\sum }_{i=l}^r{A}_l+A_{l+1}+A_{l+2}+...+A_r$ 是多少？

然而，小蓝并不知道数列中每个数的值是多少，他只知道它的 $M$ 个部分和的值

其中第 $i$ 个部分和是下标 $l_i$ 到 $r_i$ 的部分和 ${\sum }_{j=l_i}^{r_i}{A}_{l_i}+$

若不在一集合内，根据传递性，合并的时候,root_u -> u -> v -> root_v ，因为异或是无向的，所以root_u与root_v的新边的值就是uv和输入的边权z的异或和

#include<iostream>
#include<stdio.h>
#include<string.h>
#include<cstring>
#include<string>
#include<algorithm>
#include<math.h>
#include<cmath>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<deque>
#include<set>
using namespace std;
typedef long long ll;
#define IOS ios::sync_with_stdio(false),cin.tie(0) 
#define _for(i,a,b) for(int i=(a) ;i<=(b) ;i++)
#define _rep(i,a,b) for(int i=(a) ;i>=(b) ;i--)
#define mst(v,s) memset(v,s,sizeof(v))
#define pii pair<int ,int >
#define pb(v) push_back(v)
#define all(v) v.begin(),v.end()
#define int long long
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define endl "\\n"
#define fi first
#define se second
#define ls p<<1
#define rs p<<1|1
#define lson p<<1,l,mid
#define rson p<<1|1,mid+1,r
#define AC return 0
const int N=1e5+10;
const int mod=1e9+7;
const double eps=1e-8;
int n,m;
int fa[N],g[N];
int find(int x)

    if( fa[x] == x)  return x;
    int t = find(fa[x]);
    g[x] ^= g[fa[x]];
    return fa[x] = t;

ll qsm(int a,int b  )

    int ans=1,temp=a;
    while( b )
    
        if( b&1 ) ans = (ans * temp )%mod;
        temp = (temp * temp)%mod;
        b>>=1;
    
    return ans;

signed main()

#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif  
    IOS;
    cin>>n>>m;
    _for(i,1,n) fa[i]=i;
    _for(i,1,m)
    
        int x,y,z;cin>>x>>y>>z;
        int fx = find(x);
        int fy = find(y);
        int temp = g[x]^g[y];
        z^=1;
        if( fx!=fy )
        
            fa[fx] = fy;
            g[fx] = g[x]^g[y]^z;
        
        else//如果是一类，x,y,fy三元环异或为0
        
            if( temp^z ) return cout<<0<<endl,0;
        
    
    int tot=0;
    _for(i,1,n)
    
        if( i==find(i) ) tot++;
    
    int ans = qsm(2,tot-1);
    cout<<ans<<endl;
    AC;