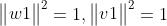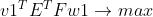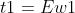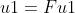偏最小二乘(PLS)原理分析&Python实现
Posted Dfreedom.
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了偏最小二乘(PLS)原理分析&Python实现相关的知识,希望对你有一定的参考价值。
目录
5.4 为什么要计算残差矩阵?为什么要不停地用残差矩阵替换原来的自变量和因变量;
1 偏最小二乘的意义
回归是研究因变量对自变量的依赖关系的一种统计分析方法,目的是通过自变量的给定值来估计或预测因变量的值。
当自变量只有一个时,常用的回归方法有一元线性回归(SLR);当自变量有多个时,常用的回归方法有多元线性回归(MLR)、主成分回归(PCR)、偏最小二乘回归(PLS)等,这几种回归方法的联系和区别如下:

从中可以看出,偏最小二乘是主成分分析+线性回归的合体,集合了两者的优点。一般来说,能用主成分分析,就一定能用偏最小二乘。当数据量小,甚至比变量维数还小,而相关性又比较大时使用,偏最小二乘是优于主成分回归。
2 PLS实现步骤
设自变量矩阵是X,因变量矩阵是Y:
① 标准化自变量矩阵和因变量矩阵,标准化后的矩阵是E和F;
② 求解自变量和因变量的第一主成分t1、u1;
③ 建立自变量E、因变量E和第一主成分t1、u1的回归方差,并计算残差矩阵E1、F1;
④ 用E1、F1代替E、F形成新的自变量、因变量,求解新的自变量和因变量的第一主成分t2、u2,即为原来自变量和因变量的第二主成分。
⑤ 建立新的自变量E1、因变量F1(残差矩阵)和第二主成分t2、u2的回归方程,并计算残差矩阵E2,F2;
⑥ 重复④、⑤步直至求出所有的主成分或者满足条件为止;
⑦ 交叉性检验,确定满足条件的主成分个数;
⑧ 建立回归方程,计算出回归系数。
3 弄懂PLS要回答的问题
① PCA的原理;
② 为什么要对X、Y标准化;
③ 如何求自变量和因变量的第一主成分;
④ 为什么要计算残差矩阵?为什么要不停地用残差矩阵替换原来的自变量和因变量;
⑤ 为什么要进行交叉性检验?
4 PLS的原理分析
从PLS的求解步骤可以看出,有两个关键点:
① 求解自变量和因变量的主成分;
② 求解回归系数。
4.1 自变量和因变量的主成分求解原理
设有p个自变量,q个以因变量,样本点个数为n,则可以得到自变量和因变量的数据表:
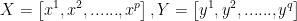
其中, 和
和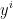 是n维列向量。
是n维列向量。
偏最小二乘的思想是求解主成分的同时要保证自变量和因变量的相关性最大。即求解X的主成分t1和Y的主成分u1,t1和u1需要满足如下要求:
(1) t1和u1应尽可能大地携带他们各自数据表中的变异信息;
(2) t1与u1的相关程度能够达到最大。
从上述原理可以看出,PLS和PCA求解主成分都是一个目标函数最大值求解的问题。区别在于两者的目标函数不一样。所以同样地,PLS求解主成分有关键的两个步骤:
1、确定目标函数;
2、求解目标函数取最大值时的投影轴w1和v1。
4.1.1 确定目标函数
① 要使主成分t1尽可能携带X的信息或者u1尽可能携带Y的信息,则有:
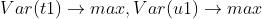
② 要使主成分t1和u1之间的相关程度最高,则有:
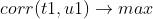
要同时满足以上两个要求,则目标函数可表示成:
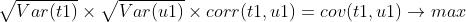
因为t1、u1分别是X、Y投影得到,设t投影轴为w1、v1,则有:
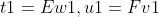
又w1、v1为方向向量,且E、F已经标准化,列向量的均值为0,则目标函数可转换为:
其中,
4.1.2 投影轴w1和v1的求解
投影轴w1和 v1求解的问题,可以描述为:
已知自变量和因变量标准化后的数据表E和F,求投影轴w1、v1使得:
其中,
这是一个条件极值的问题,可以采用拉格朗日乘子法求解,构造拉格朗日函数:
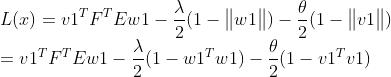
对v,w求偏导数:
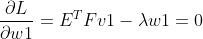
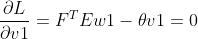
两边同时乘以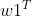 、
、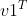 ,则有:
,则有:
所以有: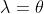 ,将
,将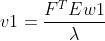 带入上述方程可得:
带入上述方程可得:
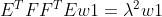
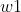 是矩阵
是矩阵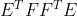 最大特征值值对应的特征向量,求出
最大特征值值对应的特征向量,求出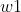 就可求出
就可求出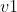 。
。
至此就可以求解出自变量和因变量的第一主成分:
4.2 求解回归系数
建立E、F和t1、u1之间的回归方程:
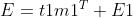
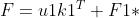
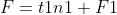
式中,m1、k1、n1回归系数,E1、F1*、F1为残差矩阵。回归系数计算公式为:
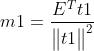
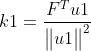
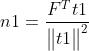
采用残差矩阵E1、F1代替E、F继续求解,即为第二主成分t2、u2。直到求出所有主成分或者满足要求(后面说明)。
设E的秩为A,则有:
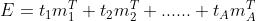
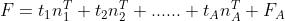
由于t1、t2、......、tA都可以表示成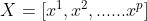 的线性组合,所以可得:
的线性组合,所以可得:
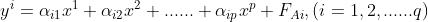
其中,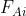 为残差矩阵的第
为残差矩阵的第 列。
列。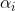 为第
为第 列因变量对应的回归系数。
列因变量对应的回归系数。
本章小结:
设自变量X=
,Y=
,
为列向量。X、Y标准化以后的矩阵为E、F。
1、第一主成分的投影轴是矩阵
最大特征值对应的特征向量;
2、求解残差矩阵E1、F1,第二成分是矩阵
最大特征值对应的特征向量;
3、以此类推,可以求出第三、四.........主成分。
4、用因变量是主成分的线性组合,主成分是自变量的线性组合,以此可得出回归系数。
5 第3章问题解答
5.1 PCA原理
要学习PLS,弄懂PCA的原理是前提条件:
主成分分析(PCA)原理分析&Python实现_Dfreedom.的博客-CSDN博客
5.2 为什么要对X、Y标准化?
当行数等于样本数,列数等于特征数时,标准化是按列进行的,分为两步:
① 每一列先减去每一列的均值;
② 每一列再除以每一列标准差。
可以看出和PCA的处理有点差别,PCA只进行了第一步(去均值)。PLS的去均值和PCA的去均值理由是一样的:目标函数的化简是基于每一列的均值为0求出的:
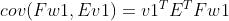
求解目标函数的这个等式成立的前提是E和F去均值。
那为什么还要除以标准差呢?为什么PCA不是必须要除以标准差呢?
① PLS求解时需要考虑自变量和因变量的相关性,协方差作为描述X和Y相关程度的量,在同一物理量纲之下有一定的作用,但同样的两个量采用不同的量纲使它们的协方差在数值上表现出很大的差异。所以需要将除以标准差将自变量和因变量统一在同一个量纲里;
② PCA在求解时不需要考虑相关性,所以只是中心化就足够。当然也可以标准化。
即:PCA可以只中心化,也可以继续标准化,PLS就必须标准化,不能只是中心化。
5.3 如何求自变量和因变量的第一主成分
设自变量和因变量标准化后的矩阵是E和F,从4.1章节的推导过程可知,自变量的第一主成分的投影轴w1是矩阵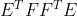 最大特征值值对应的特征向量,求出w1可根据公式
最大特征值值对应的特征向量,求出w1可根据公式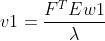 求出因变量第一主成分的投影轴v1。知道投影轴以后就可以根据投影的计算公式得到第一主成分:
求出因变量第一主成分的投影轴v1。知道投影轴以后就可以根据投影的计算公式得到第一主成分:
5.4 为什么要计算残差矩阵?为什么要不停地用残差矩阵替换原来的自变量和因变量;
如果只是根据目标函数求解出自变量和因变量的主成分,会出现与CCA一样的不能由X到Y映射的问题。可以从误差的角度来理解,在回归分析中,得到回归系数以后,用自变量去估计因变量会存在误差,称之为残差,如下公式:
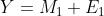
式中,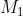 为第一主成分和回归系数的乘积,E为残差矩阵。为了减小估计误差也就是残差,继续求解残差的第一主成分,将残差用表示成自变量的线性组合,从而就可以减小回归误差:
为第一主成分和回归系数的乘积,E为残差矩阵。为了减小估计误差也就是残差,继续求解残差的第一主成分,将残差用表示成自变量的线性组合,从而就可以减小回归误差:

式中,Ek是残差,k是选择的主成分个数。显而易见k越大,残差就越小,所以一般情况下,只要迭代足够多的次数,就可以将回归误差减小到满足目标要求。M1称为第一主成分,M2称为第二主成分,以此类推。
5.5 为什么要进行交叉性检验?
原因:在许多情形下,偏最小二乘回归方程并不需要选用全部的成分进行回归建模,而是可以象在主成分分析一样,采用截尾的方式选择前m 个成分,仅用这m 个后续的成分就可以得到一个预测性较好的模型。事实上,如果后续的成分已经不能为解释因变量提供更有意义的信息时,采用过多的成分只会破坏对统计趋势的认识,引导错误的预测结论。
交叉性检验的判定条件是预测平方误差和与误差平方和的比值,本文不作详细的介绍,有兴趣的可以阅读文章末尾的参考链接。
6 PLS代码实现——Python
程序流程图:
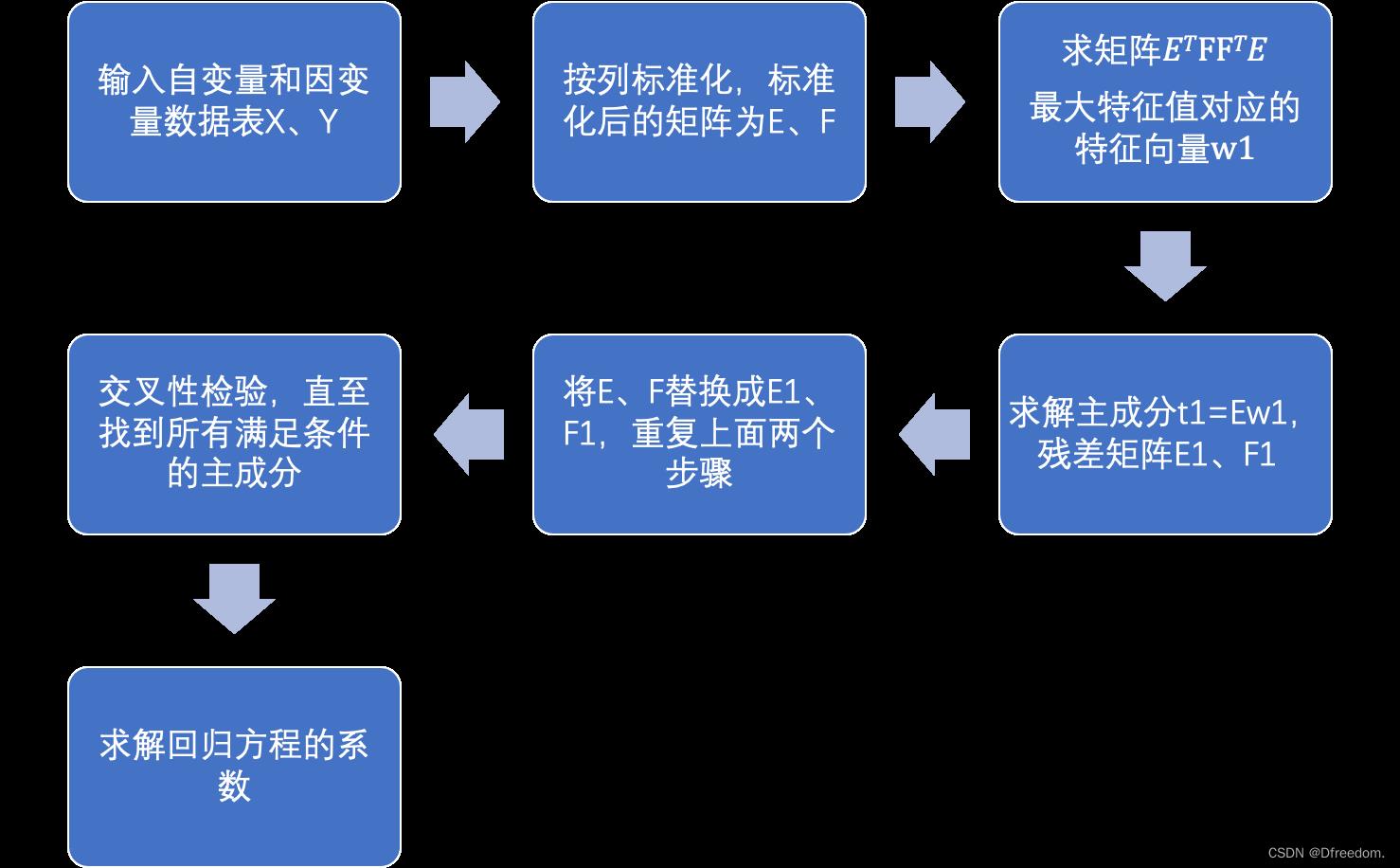
Python代码:
import numpy as np
x1=[191,189,193,162,189,182,211,167,176,154,169,166,154,247,193,202,176,157,156,138]
x2=[36,37,38,35,35,36,38,34,31,33,34,33,34,46,36,37,37,32,33,33]
x3=[50,52,58,62,46,56,56,60,74,56,50,52,64,50,46,62,54,52,54,68]
y1=[5,2,12,12,13,4,8,6,15,17,17,13,14,1,6,12,4,11,15,2]
y2=[162,110,101,105,155,101,101,125,200,251,120,210,215,50,70,210,60,230,225,110]
y3=[60,60,101,37,58,42,38,40,40,250,38,115,105,50,31,120,25,80,73,43]
#-----数据读取
data_raw=np.array([x1,x2,x3,y1,y2,y3])
data_raw=data_raw.T #输入原始数据,行数为样本数,列数为特征数
#-----数据标准化
num=np.size(data_raw,0) #样本个数
mu=np.mean(data_raw,axis=0) #按列求均值
sig=(np.std(data_raw,axis=0)) #按列求标准差
data=(data_raw-mu)/sig #标准化,按列减去均值除以标准差
#-----提取自变量和因变量数据
n=3 #自变量个数
m=3 #因变量个数
x0=data_raw[:,0:n] #原始的自变量数据
y0=data_raw[:,n:n+m] #原始的变量数据
e0=data[:,0:n] #标准化后的自变量数据
f0=data[:,n:n+m] #标准化后的因变量数据
#-----相关矩阵初始化
chg=np.eye(n) #w到w*变换矩阵的初始化
w=np.empty((n,0)) #初始化投影轴矩阵
w_star=np.empty((n, 0)) #w*矩阵初始化
t=np.empty((num, 0)) #得分矩阵初始化
ss=np.empty(0) #或者ss=[],误差平方和初始化
press=[] #预测误差平方和初始化
Q_h2=np.zeros(n) #有效性判断条件值初始化
#-----求解主成分
for i in range(n): #主成分的总个数小于等于自变量个数
#-----求解自变量的最大投影w和第一主成分t
matrix=e0.T@f0@f0.T@e0 #构造矩阵E'FF'E
val,vec=np.linalg.eig(matrix) #计算特征值和特征向量
index=np.argsort(val)[::-1] #获取特征值从大到小排序前的索引
val_sort=val[index] #特征值由大到小排序
vec_sort=vec[:,index] #特征向量按照特征值的顺序排列
w=np.append(w,vec_sort[:,0][:,np.newaxis],axis=1) #储存最大特征向量
w_star=np.append(w_star,chg@w[:,i][:,np.newaxis],axis=1) #计算 w*的取值
t=np.append(t,e0@w[:,i][:,np.newaxis],axis=1) #计算投影
alpha=e0.T@t[:,i][:,np.newaxis]/(t[:,i]@t[:,i]) #计算自变量和主成分之间的回归系数
chg=chg@(np.eye(n)-(w[:,i][:,np.newaxis]@alpha.T)) #计算 w 到 w*的变换矩阵
e1=e0-t[:,i][:,np.newaxis]@alpha.T #计算残差矩阵
e0=e1 #更新残差矩阵
#-----求解误差平方和ss
beta=np.linalg.pinv(t)@f0 #求回归方程的系数,数据标准化,没有常数项
res=np.array(f0-t@beta) #求残差
ss=np.append(ss,np.sum(res**2))#残差平方和
#-----求解残差平方和press
press_i=[] #初始化误差平方和矩阵
for j in range(num):
t_inter=t[:,0:i+1]
f_inter=f0
t_inter_del=t_inter[j,:] #把舍去的第 j 个样本点保存起来,自变量
f_inter_del=f_inter[j,:] #把舍去的第 j 个样本点保存起来,因变量
t_inter= np.delete(t_inter,j,axis=0) #删除自变量第 j 个观测值
f_inter= np.delete(f_inter,j,axis=0) #删除因变量第 j 个观测值
t_inter=np.append(t_inter,np.ones((num-1,1)),axis=1)
beta1=np.linalg.pinv(t_inter)@f_inter # 求回归分析的系数,这里带有常数项
res=f_inter_del-t_inter_del[:,np.newaxis].T@beta1[0:len(beta1)-1,:]-beta1[len(beta1)-1,:] #计算残差
res=np.array(res)
press_i.append(np.sum(res**2)) #残差平方和,并存储
press.append(np.sum(press_i)) #预测误差平方和
#-----交叉有效性检验,判断主成分是否满足条件
Q_h2[0]=1
if i>0:
Q_h2[i]=1-press[i]/ss[i-1]
if Q_h2[i]<0.0975:
print('提出的成分个数 r=',i+1)
break
#-----根据主成分t计算回归方程的系数
beta_Y_t=np.linalg.pinv(t)@f0 #求Y*关于t的回归系数
beta_Y_X=w_star@beta_Y_t#求Y*关于X*的回归系数
mu_x=mu[0:n] #提取自变量的均值
mu_y=mu[n:n+m] #提取因变量的均值
sig_x=sig[0:n] #提取自变量的标准差
sig_y=sig[n:n+m] #提取因变量的标准差
ch0=mu_y-mu_x[:,np.newaxis].T/sig_x[:,np.newaxis].T@beta_Y_X*sig_y[:,np.newaxis].T#算原始数据回归方程的常数项
beta_target=np.empty((n,0)) #回归方程的系数矩阵初始化
for i in range(m):
a=beta_Y_X[:,i][:,np.newaxis]/sig_x[:,np.newaxis]*sig_y[i]#计算原始数据回归方程的系数
beta_target=np.append(beta_target,a,axis=1)
target=np.concatenate([ch0,beta_target],axis=0) #回归方程的系数,每一列是一个方程,每一列的第一个数是常数项
print(target)参考链接:
偏最小二乘法回归(Partial Least Squares Regression) - JerryLead - 博客园
【建模应用】PLS偏最小二乘回归原理与应用 - pigcv - 博客园
基于偏最小二乘及最小二乘支持向量机的人工加糙渠道糙率预测模型研究(葛赛,赵涛等)


基于偏最小二乘及最小二乘支持向量机的人工加糙渠道糙率预测模型研究
葛赛 1,赵涛 1,吴思 2,吴洋锋 1
( 1.新疆农业大学 水利与土木工程学院,乌鲁木齐 830052; 2.黄河勘测规划设计有限公司,郑州 450003)
作者简介
葛赛(1993-),女,河北廊坊人,主要从事水工水力学及内陆河流水沙运动反面研究。
赵涛( 1976-),男,河南安阳人,满族,副教授,主要从事水力学及河流动力学方面研究。




摘要
影响渠道糙率的因素相当复杂,且因素间又存在一定的相关关系。为取得更为精确的糙率预测效果,采用偏最小二乘( PLS)法对影响人工加糙渠道糙率的因素进行分析,提取影响自变量的重要成分,结合最小二乘支持向量机( LSSVM)建立了人工加糙渠道糙率预测模型。结合实例,通过对某人工加糙渠道相关试验数据进行 PLS-LSSVM 模型的训练及预测,并将预测结果与单独使用 PLS、 LSSVM 及公式法的预测结果进行对比,其结果显示:基于 PLS-LSSVM 模型的预测平均绝对百分比误差 MAPE 为 1.38%,均方根误差 RMSE 为 2.24*10^-4 ,预测精度均优于 PLS、 LSSVM 及公式法的预测结果。结果表明,将 PLS 与LSSVM 相结合的 PLS-LSSVM 模型,综合了 PLS 与 LSSVM 各自的优势,应用 PLS-LSSVM 模型可有效进行人工加糙渠道糙率的预测。
关键词
偏最小二乘( PLS);最小二乘支持向量机( LSSVM);人工加糙渠道;糙率;预测
Study of artificial rough channel roughness prediction model based on partial least square and least square support vector machine
GE Sai1, ZHAO Tao1, WU Si2, WU Yangfeng1
(1.College of Water Conservancy and Civil Engineering, Xinjiang Agricultural University, Urumqi 830052,China; 2.Yellow River Engineering Consulting Co., Ltd, Zhengzhou 450003, China)
The factors that affect the roughness of channel are quite complex, and there is a certain correlation between factors. In order to obtain a more accurate prediction of the roughness, the partial least squares (PLS) method was used to analyze the factors that affect the roughness of artificial rough channel, and the important components that affect the independent variable were extracted, then the roughness prediction model of artificial rough channel was established based on least square support vector machine (LSSVM). Combining with the example, through the training and prediction of PLS-LSSVM model test data related to artificial rough channel, and the prediction results are compared with the prediction results of PLS, LSSVM and formula alone, the results show that the average absolute percentage error (MAPE) of prediction based on PLS-LSSVM model is 1.38%, and the root mean square error (RMSE) is 2.24*10^-4 , the prediction accuracy is better than that of PLS, LSSVM and formula method. The results show that the PLS-LSSVM model which combines PLS and LSSVM combines the advantages of PLS and LSSVM, PLS-LSSVM model can effectively predict the roughness of artificial rough channel.
Key words
partial least squares (PLS); least square support vector machine (LSSVM); artificial rough channel; roughness; prediction
基金项目
新疆维吾尔自治区自然科学基金项目(2015211A025)

糙率[1]与河流阻力有关,是衡量渠道边壁粗糙程度对运动水流产生影响的一个无量纲数,其值重要且敏感,糙率的精确取值是明渠水流的水力计算向精准方向发展拟解决的关键问题之一。明渠糙率研究可分为两个方向,即天然渠道糙率和人工渠道糙率。人工渠道以其较为规则的结构形式及沿程均匀的粗糙程度,简化天然渠道复杂多变的水力要素,同时加糙处理后的人工渠道增加了多种边壁粗糙条件,更易于对糙率进行更为全面深入的研究[2-3]。
多年以来,有许多学者[4-9]从分析糙率与关键水力要素的相关关系出发,力求推导出普遍适用的糙率经验公式,但取得的成果有限。随着计算机技术的发展,有学者打破糙率研究的传统思维方式,通过构建数学模型进行糙率预测并取得丰硕成果。 Becker 等[10-11]提出将改进的单纯形算法用于糙率数学模型的建立,金忠青等[12-13]采用复合形法构建河网糙率预测模型,程伟平等[14-15]引入广义逆理论及带参数的卡尔曼滤波构建糙率预测模型,雷燕等[16]运用遗传算法建立糙率数学模型,辛小康等[17]对遗传算法优化构建预测模型,涨潮等[18-19]基于 BP 神经网络并对算法进行改进构建糙率数学模型。虽然糙率预测模型依旧在不断完善创新,但仍存在多种限制因素,例如模型需大量样本数据进行学习训练且运算效率较低,极易陷入局部最优状态,而且模型参数的选择难度较大将会影响计算精准度。最小二乘支持向量机(Least Square Support Vector Machine,简称 LSSVM)是由 Suykens 等[20-22]提出的对标准支持向量机( Support Vector Machine, 简称 SVM) [23]的改进优化,除拥有 SVM 解决小样本、非线性、避免陷入局部极值、参数寻优方法简便等优势外,又通过在目标函数中引入误差平方和项进一步降低计算复杂度提高运算效率,减小 SVM 迭代误差可能对算法精度产生的影响。本文提出应用 LSSVM 进行人工加糙渠道糙率预测,并预先对多个主要影响因素进行偏最小二乘( Partial Least Squares,简称 PLS) [24]分析,提取影响糙率的重要成分,降低无关成分及变量间不独立对模型的影响。
因此,本文采用 PLS 法对数据预处理,结合 LSSVM 建立模型,构建基于偏最小二乘及最小二乘支持向量机(简称 PLS-LSSVM)的人工加糙渠道糙率预测模型。并以某矩形人工加糙渠道为例进行模型训练及预测,验证模型可靠性及适用性。
1

模型算法原理
1.1
偏最小二乘(PLS)算法
偏最小二乘是一种用于多元统计数据分析的新型算法,在消除变量间相关性问题及提取变量的重要信息方面表现突出,综合了典型相关分析、主成分分析及多元线性回归分析在数据分析处理方面的优势于一体。根据本文实际情况,针对多自变量及单因变量进行研究,假设样本数为 m,自变量个数为 n,
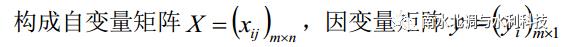
算法具体计算步骤如下:
进行数据标准化处理。为将数据的不同特征以相同的尺度来表示,减小不同变量在量纲及数量级差异上对数据信息的影响,对自变量 X 与因变量 y 进行标准化处理。


提取成分。自变量矩阵 X 为多变量,对矩阵 X 提取成分 t1。其中, t1 应最大限度的承载矩阵 X 的相关变异信息情况,且 t1 需满足公式:


1.2
最小二乘支持向量机(LSSVM)算法
最小二乘支持向量机是标准支持向量机的一种优化算法,通过用等式约束代替不等式约束,将误差平方和损失函数作为训练集的经验损失,把较难处理的二次规划问题转化为对线性方程组的求解问题。与标准支持向量机所建模型相比,最小二乘支持向量机收敛精度及运算效率方面具有绝对优势。内部算法原理如下:
设样本训练集为{ xi, yi}, xi∈Rd, yi∈R,( i=1,2,…n; d 为 Rd 空间的维数)。针对非线性问题,引入非线性映射,将样本数据从原空间映射到高维特征空间,构造出线性回归函数:

通过引入拉格朗日函数进行优化目标函数问题的求解,得到:


求解该线性方程组得到 a 和 b,则线性回归函数为:

2

基于 PLS-LSSVM 的人工
加糙渠道糙率预测模型
2.1
PLS-LSSVM 模型
在处理实际工程问题时,经常会遇到存在多种影响因素的情况,直接将数据带入到模型中不仅会干扰模型计算的精度,甚至可能会严重影响模型运算效率。偏最小二乘 PLS 法通过对原变量进行预处理,提取出反映变量信息的重要成分,这些新提取的成分包含了原变量的所有信息,且各个成分间相互独立,消除了原变量间存在的线性相关的情况,同时,重要成分的个数小于原变量的个数,实现了对原数据组的降维。最小二乘支持向量机 LSSVM 是一种优质的机器学习方法,其可通过对训练集进行学习训练,掌握事物内部的变化规律,从而对测试集做出客观合理的预测。偏最小二乘及最小二乘支持向量机 PLS-LSSVM 模型是将偏最小二乘 PLS 与最小二乘支持向量机 LSSVM 相结合,首先运用 PLS 法对样本数据进行预处理,并将预处理提取的重要成分作为 LSSVM 的输入,以减小模型对数据的识别难度,进一步发挥 LSSVM 在预测方面的优势。
2.2
人工加糙渠道糙率物理模型
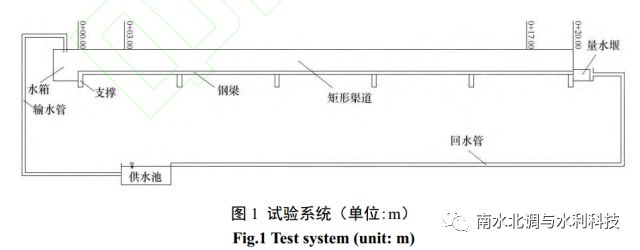
某人工渠道长 20 m、 宽 0.4 m、深 0.3 m,断面形状为矩形,底坡为可自动调节装置,采用 PVC 材质制作。 试验系统由供水装置、静水箱、可进行坡度调节的渠道、尾门、量水堰、回水装置等组成, 试验系统见图 1。测量段选取去除渠道首尾各 3 m 的中间部分,每间隔 1 m 作为一个测量断面,每个断面布设左、中、右三个测点。渠道通过保持光滑壁面条件及在底部、两侧粘贴粒径 d 为 1~2 mm、 2~3 mm、 3~5 mm 砂粒的方式,模拟出绝对粗糙度Δ 为 0.015 mm、 1.5 mm、 2.5 mm、 4.0 mm 的 4 种不同边壁条件。在满足某一边壁条件下,调节 0.004~0.03 共 8 种不同底坡,设置 12~41 L/s 共 10 组不同流量, 采用水位测针量测每个测点的水深从而得出渠道的平均水深,根据相关已知条件计算得到各关键水力要素及糙率值,试验共获得 320 组试验数据。
2.3
基于 PLS-LSSVM 的人工加糙渠道糙率预测模型建立
划分训练集及测试集。由前期研究成果[25-26]可知,影响人工加糙渠道糙率的主要因素间存在相关性,冗余信息会对预测模型产生干扰。将绝对粗糙度 Δ( x1)、佛汝德数 Fr( x2)、渠道平均水深 h( x3)、底坡 i( x4)作为 PLS-LSSVM 模型的自变量,人工加糙渠道糙率 n值( y)作为 PLS-LSSVM 模型的因变量, 构成数据矩阵 A 为 320 5。将 320 组样本数据随机选取 240 组作为训练集,其余 80 组数据作为测试集。

选取核函数及参数。将径向基函数(Radial Basis Function,简称 RBF)作为核函数,其在此模型条件下表现出较其他核函数更为出色的泛化能力,并且已在许多领域广泛应用。采用交叉验证法进行参数寻优,得到正则化参数 γ=618.9333,核参数 σ2=0.1379。
模型训练预测。对已构建好的 PLS-LSSVM 模型进行学习训练,并对测试集进行预测。选取平均绝对百分比误差 MAPE 及均方根误差 RMSE 作为模型精确性度量标准,反映预测值和观测值之间的偏差程度,对预测结果可靠性进行评价。公式分别如下:

2.4
基于 PLS-LSSVM 的人工加糙渠道糙率预测模型结果及分析
采用 PLS 法对人工加糙渠道糙率相关样本数据进行预处理,并将预处理后的结果作为LSSVM 的输入。通过对组合模型 PLS-LSSVM 进行学习训练,在模型掌握事物相应的内部规律后,对测试集做出预测。为验证组合模型的预测精度,将预测结果分别与单独使用 PLS、LSSVM 模型的预测结果进行对比,同时,为更进一步说明预测模型的优势,将模型预测效果与公式法的预测效果进行对比。借鉴李榕[27]基于量纲分析法及利用大量的试验数据推求的适用于明渠均匀流的糙率回归方程形式,如式( 23)所示,通过拟合可知,式(23)中的系数 n0 及α与底坡 i 具有良好的对数函数关系。拟合得到的 4 种不同边壁条件下的系数 n0及α如表 1 所示, 并将其分别带入式(23)中进行糙率预测,总的预测效果对比如图 2 及表 2 所示。

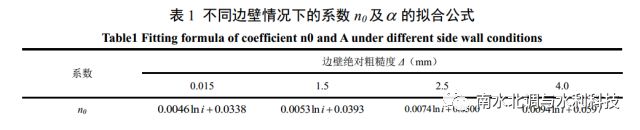
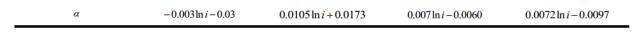
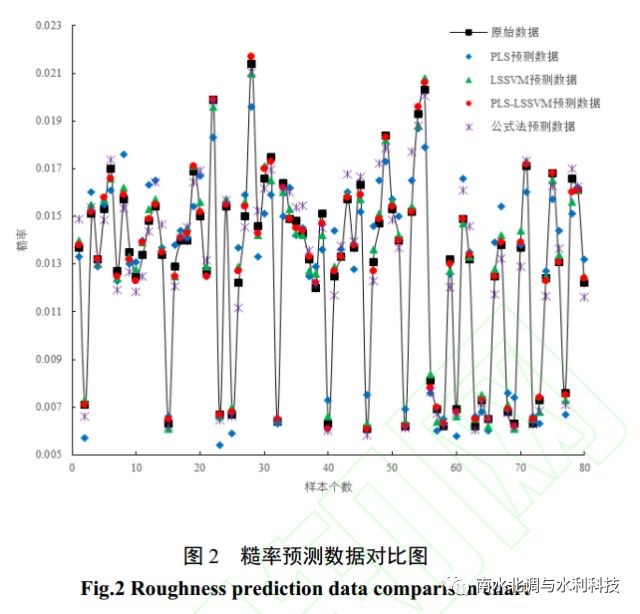
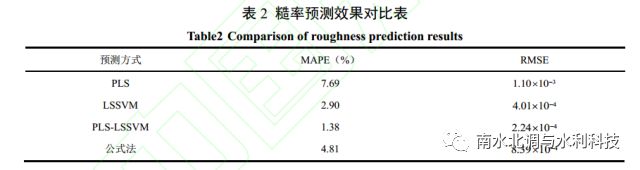
在明渠水流的水力计算中,对糙率取值的精度要求较为严格。采用 PLS 法进行糙率预测,预测数据的平均绝对百分比误差 MAPE 为 7.69%,均方根误差 RMSE 为1.10*10^3 ,而采用公式法进行糙率预测,预测数据的平均绝对百分比误差 MAPE 为 4.81%,均方根误差RMSE 为8.39*10^4,预测精度较 PLS 法有了一定程度的提升。 LSSVM 模型预测数据的平均绝对百分比误差 MAPE 为 2.90%,均方根误差 RMSE 为 4.01*10^4 ,与公式法的预测结果相比,在预测精度方面有了进一步的提升,但 LSSVM 模型将样本数据直接作为模型的输入,可能会对模型训练产生干扰从而影响预测结果。 PLS-LSSVM 模型融合了 PLS 及 LSSVM 模型的优点,预测数据的平均绝对百分比误差 MAPE 为 1.38%,均方根误差 RMSE 为2.24*10^4 ,预测性能较单独使用 LSSVM 模型有了更进一步的提升。由此可见,在对人工加糙渠道的研究过程中, PLS-LSSVM 模型相对于 PLS、 LSSVM 模型及公式法来说,更适合用于进行人工加糙渠道糙率方面的相关预测。
2.5
不同变量组合下的 PLS-LSSVM 模型预测效果对比
以在人工加糙渠道糙率预测方面表现良好的 PLS-LSSVM 作为预测模型,基于上文选用的作为模型输入的自变量组合形式: 绝对粗糙度 Δ(x1)、佛汝德数 Fr(x2)、渠道平均水深h(x3)、底坡 i(x4),尝试另外 3 种自变量组合形式: 绝对粗糙度 Δ(x1)、佛汝德数 Fr(x2)、渠道平均水深 h(x3), 绝对粗糙度 Δ(x1)、渠道平均水深 h(x2)、底坡 i(x3), 绝对粗糙度Δ(x1)、渠道平均水深 h(x2)进行模型的训练及预测,不同变量组合下的预测效果对比如表 3 所示。
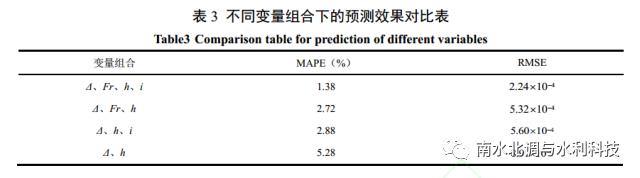
从表 3 中可以看出,新选用的 3 种变量组合形式下模型预测精度均低于原变量组合形式下的预测精度。其中,同时去除变量 Fr、 i 的组合形式对模型预测精度影响最大,去除变量Fr 比去除变量 i 的组合形式对模型预测精度的影响更大。
3

结论
(1)
文章采用偏最小二乘及最小二乘支持向量机 PLS-LSSVM 模型,进行人工加糙渠道糙率的相关预测。对影响人工加糙渠道糙率的主要因素进行 PLS 重要成分的提取,消除变量间的多重相关性,综合全面描述事物的本质因素,并将提取的重要成分作为最小二乘支持向量机 LSSVM 的输入,减小数据对模型的干扰,更有助于模型的训练及预测。
(2)
预测结果显示,PLS-LSSVM 模型预测数据的平均绝对百分比误差 MAPE 为 1.38%,均方根误差 RMSE 为 2.24*10^4 ,优于单独使用 PLS 模型、公式法的预测效果,较优于单独使用 LSSVM 的预测效果。 PLS-LSSVM 模型综合了 PLS、 LSSVM 各自的优势性能,进一步提高了预测精度。
(3)
选取更为合理的糙率,提高明渠水流水力计算的精度,不仅有利于渠道正常投入运行,更有利于对其进行科学的规划与管理。选取适用的自变量组合形式,基于 PLS-LSSVM模型进行渠道糙率预测,具有良好的应用前景。



参考文献略
本文内容为录用首发版,定稿请参见《南水北调与水利科技》刊文。
本期编辑: 阿丹、海超、檬檬
免责声明:遵循微信公众平台关于保护原创的各项举措。推送文章可能未能事先与原作者取得联系,或无法查证真实原作者,若涉及版权问题,请原作者留言联系我们。经核实后,我们会及时删除或者注明原作者及出处。

《南水北调与水利科技》
共筑学术交流新天地 同谱人水和谐新篇章
以上是关于偏最小二乘(PLS)原理分析&Python实现的主要内容,如果未能解决你的问题,请参考以下文章