如何求完全二叉树的度为1的结点个数

Posted 2023-04-07

方法1：

根据二叉树性质3可以反推度为1的结点个数，设完全二叉树的总结点个数为n,度为0的结点个数为n0,度为1的结点个数为n1,度为2的结点个数为n2 则

n=n0+n1+n2

n1=n-n0-n2

方法2：

我们知道完全二叉树的特点，它缺少结点时总是出现在叶子层(即最下面一层)的右子树开始连续缺少。

我们设完全二叉树的深度为k(k>1)，则从第1层至第k-1层的结点总数为2^k-1个(根据二叉树性质2计算出来)且一定是奇数，所以完全二叉树最下面一层的最左子树开始计算,如果出现偶数个结点则不存在度为1的结点,反之度为1的结点个数一定是1。

若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。

(1)所有的叶结点都出现在第k层或k-l层（层次最大的两层）

(2)对任一结点，如果其右子树的最大层次为L，则其左子树的最大层次为L或L+l。

一棵二叉树至多只有最下面的两层上的结点的度数可以小于2，并且最下层上的结点都集中在该层最左边的若干位置上，则此二叉树成为完全二叉树，并且最下层上的结点都集中在该层最左边的若干位置上，而在最后一层上，右边的若干结点缺失的二叉树，则此二叉树成为完全二叉树。

扩展资料：

如果一棵具有n个结点的深度为k的二叉树，它的每一个结点都与深度为k的满二叉树中编号为1~n的结点一一对应，这棵二叉树称为完全二叉树。

可以根据公式进行推导，假设n0是度为0的结点总数（即叶子结点数），n1是度为1的结点总数，n2是度为2的结点总数，则 ：

①n= n0+n1+n2 （其中n为完全二叉树的结点总数）；又因为一个度为2的结点会有2个子结点，一个度为1的结点会有1个子结点，除根结点外其他结点都有父结点，

②n= 1+n1+2*n2 ；由①、②两式把n2消去得：n= 2*n0+n1-1，由于完全二叉树中度为1的结点数只有两种可能0或1，由此得到n0=n/2 或 n0=(n+1)/2。

简便来算，就是 n0=n/2，其中n为奇数时（n1=0）向上取整；n为偶数时（n1=1）。可根据完全二叉树的结点总数计算出叶子结点数。

参考资料：百度百科---完全二叉树

参考技术A

方法1：

根据二叉树性质3可以反推度为1的结点个数，设完全二叉树的总结点个数为n,度为0的结点个数为n0,度为1的结点个数为n1,度为2的结点个数为n2 则

  n=n0+n1+n2

  n1=n-n0-n2

方法2：

  我们知道完全二叉树的特点，它缺少结点时总是出现在叶子层(即最下面一层)的右子树开始连续缺少。我们设完全二叉树的深度为k(k>1),则从第1层至第k-1层的结点总数为2^k-1个(根据二叉树性质2计算出来)且一定是奇数，所以完全二叉树最下面一层的最左子树开始计算,如果出现偶数个结点则不存在度为1的结点,反之度为1的结点个数一定是1.

本回答被提问者和网友采纳 参考技术B 总点数为偶数时1个，否则没有

树---- 二叉树

1 树的基本概念

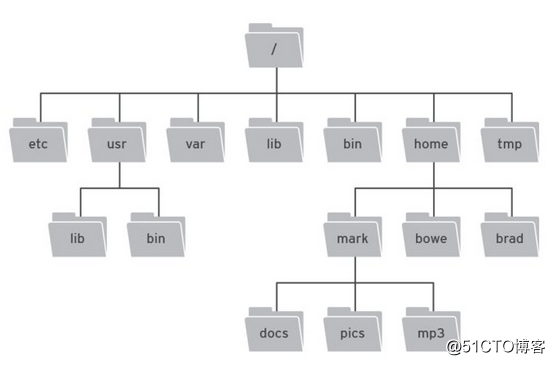
（1）树是由若干结点组成的具有层次关系的集合，非空树有且只有一个根结点（/）。

（2）某个结点及其下面所有的结点并称为以该结点为根的子树（usr及其下的所有结点就是/的一颗子树，usr是该子树的根）。

（3）结点拥有的子树的个数称为结点的度（/的度为7，home的度为3）。

（4）度为0的节点称为叶子结点（lib就是叶子结点）。

（5）树的深度就是结点的最大层数（上图中的树深度为4）。

注意：
（1）在一颗非空树上，一定会有根结点和叶子结点。当只存在一个结点时，它既是根结点也是叶子结点。

（2）在树上，父结点可以有多个孩子结点，但是除根结点外的孩子结点仅有一个父结点。