机器视觉Q&A

Posted 2023-04-07

参考技术A  A. 数据增广

 B. 提前停止训练

C. 添加Dropout

答案：ABC

A. SGD（stochatic gradient descent）

B. BGD（batch gradient descent）

C. Adadetla

D. Momentum

答案：C

【解析】

1）SGD受到学习率α影响

2）BGD受到batch规模m影响

3）Adagrad的一大优势时可以避免手动调节学习率，比如设置初始的缺省学习率为0.01，然后就不管它，另其在学习的过程中自己变化。

为了避免削弱单调猛烈下降的减少学习率，Adadelta产生了1。Adadelta限制把历史梯度累积窗口限制到固定的尺寸w，而不是累加所有的梯度平方和

4）Momentum：也受到学习率α的影响

A.惩罚了模型的复杂度，避免模型过度学习训练集，提高泛化能力

B.剃刀原理：如果两个理论都能解释一件事情，那么较为简单的理论往往是正确的

C.正则项降低了每一次系数w更新的步伐，使参数更小，模型更简单

D.贝叶斯学派的观点，认为加入了先验分布（l1拉普拉斯分布，l2高斯分布），减少参数的选择空间

答案：ABCD

【解析】A/C选项没有问题，只不过C中的"步伐"理解起来并不清晰。B/D选项是有点追本溯源的意思，剃刀原理其实是奥卡姆剃刀原理：更小的权值w，从某种意义上说，表示网络的复杂度更低，对数据的拟合刚刚好；从贝叶斯角度理解，为参数ω引入拉普拉斯先验分布的最大似然，相当于给均方误差函数加上L1正则项；为参数ω引入高斯先验分布的最大似然，相当于给均方误差函数加上L2正则项。

a.计算预测值和真实值之间的误差

b.重复迭代，直至得到网络权重的最佳值

c.把输入传入网络，得到输出值

d.用随机值初始化权重和偏差

e.对每一个产生误差的神经元，调整相应的（权重）值以减小误差

答案：dcaeb

A.惩罚了模型的复杂度，避免模型过度学习训练集，提高泛化能力

B.剃刀原理：如果两个理论都能解释一件事情，那么较为简单的理论往往是正确的

C.正则项降低了每一次系数w更新的步伐，使参数更小，模型更简单

D.贝叶斯学派的观点，认为加入了先验分布（l1拉普拉斯分布，l2高斯分布），减少参数的选择空间

答案：ABCD

【解析】A/C选项没有问题，只不过C中的"步伐"理解起来并不清晰。B/D选项是有点追本溯源的意思，剃刀原理其实是奥卡姆剃刀原理：更小的权值w，从某种意义上说，表示网络的复杂度更低，对数据的拟合刚刚好；从贝叶斯角度理解，为参数ω引入拉普拉斯先验分布的最大似然，相当于给均方误差函数加上L1正则项；为参数ω引入高斯先验分布的最大似然，相当于给均方误差函数加上L2正则项。

参考：

[正则化为什么能防止过拟合（重点地方标红了）](https://www.cnblogs.com/alexanderkun/p/6922428.html)

[【机器学习】从贝叶斯角度理解正则化缓解过拟合](https://blog.csdn.net/u014433413/article/details/78408983)

A. 220x220x5

B. 218x218x5

C. 217x217x8

D. 217x217x3

答案：B

【解析】卷积计算公式：Hout=（Himg+2Padding−Kfilterh）/S + 1；Wout=（Wimg+2Padding−Kfilterw）/S + 1。其中Padding是边界填空值，Kfilterw表示卷积核的宽度，S表示步长。

A.少于2秒

B.大于2秒

C.仍是2秒

D.说不准

答案：C

【解析】在架构中添加Dropout这一改动仅会影响训练过程，而并不影响测试过程。

A.准确率适合于衡量不平衡类别问题

B.精确率和召回率适合于衡量不平衡类别问题

C.精确率和召回率不适合于衡量不平衡类别问题

D.上述选项都不对

答案：B

A. Boosting

B. Bagging

C. Stacking

D. Mapping

答案：B

【解析】dropout的思想继承自bagging方法。

bagging是一种集成方法（ensemble methods）,可以通过集成来减小泛化误差（generalization error）。

bagging的最基本的思想是通过分别训练几个不同分类器，最后对测试的样本，每个分类器对其进行投票。在机器学习上这种策略叫model averaging。 我们可以把dropout类比成将许多大的神经网络进行集成的一种bagging方法。

1. 随机初始化感知机权重

2. 去到数据集的下一批（batch）

3. 如果预测值和输出不一致，则调整权重

4. 对一个输入样本，计算输出值

A. 1,2,3,4

B. 4,3,2,1

C. 3,1,2,4

D. 1,4,3,2

答案：D

11.【单选题】下列哪项关于模型能力（model capacity）的描述是正确的？（指神经网络模型能拟合复杂函数的能力）

A.隐藏层层数增加，模型能力增加

B. Dropout的比例增加，模型能力增加

C.学习率增加，模型能力增加

D.都不正确

答案：A

A. Logistic回归可用于预测事件发生概率的大小

B. Logistic回归的目标函数是最小化后验概率

C. SVM的目标的结构风险最小化

D. SVM可以加入正则化项，有效避免模型过拟合

答案：B

【解析】Logistic回归本质上是一种根据样本对权值进行极大似然估计的方法，而后验概率正比于先验概率和似然函数的乘积。Logistic仅仅是最大化似然函数，并没有最大化后验概率，更谈不上最小化后验概率。A正确 Logit回归的输出就是样本属于正类别的几率，可以计算出概率；C正确. SVM的目标是找到使得训练数据尽可能分开且分类间隔最大的超平面，应该属于结构风险最小化. D正确. SVM可以通过正则化系数控制模型的复杂度，避免过拟合。

A增加训练集量

B减少神经网络隐藏层节点数

C删除稀疏的特征

D SVM算法中使用高斯核/RBF核代替线性核

答案：D

【解析】一般情况下，越复杂的系统，过拟合的可能性就越高，一般模型相对简单的话泛化能力会更好一点。

B.一般认为，增加隐层数可以降低网络误差（也有文献认为不一定能有效降低），提高精度，但也使网络复杂化，从而增加了网络的训练时间和出现“过拟合”的倾向， svm高斯核函数比线性核函数模型更复杂，容易过拟合

D.径向基(RBF)核函数/高斯核函数的说明,这个核函数可以将原始空间映射到无穷维空间。对于参数 ，如果选的很大，高次特征上的权重实际上衰减得非常快，实际上（数值上近似一下）相当于一个低维的子空间；反过来，如果选得很小，则可以将任意的数据映射为线性可分——当然，这并不一定是好事，因为随之而来的可能是非常严重的过拟合问题。不过，总的来说，通过调整参数 ，高斯核实际上具有相当高的灵活性，也是 使用最广泛的核函数 之一。

A.感知准则函数

B.贝叶斯分类

C.支持向量机

D.Fisher准则

答案：ACD

【解析】

线性分类器有三大类：感知器准则函数、SVM、Fisher准则，而贝叶斯分类器不是线性分类器。

感知准则函数 ：准则函数以使错分类样本到分界面距离之和最小为原则。其优点是通过错分类样本提供的信息对分类器函数进行修正，这种准则是人工神经元网络多层感知器的基础。

支持向量机 ：基本思想是在两类线性可分条件下，所设计的分类器界面使两类之间的间隔为最大，它的基本出发点是使期望泛化风险尽可能小。（使用核函数可解决非线性问题）

Fisher准则 ：更广泛的称呼是线性判别分析（LDA），将所有样本投影到一条远点出发的直线，使得同类样本距离尽可能小，不同类样本距离尽可能大，具体为最大化“广义瑞利商”。

根据两类样本一般类内密集，类间分离的特点，寻找线性分类器最佳的法线向量方向，使两类样本在该方向上的投影满足类内尽可能密集，类间尽可能分开。这种度量通过类内离散矩阵 Sw和类间离散矩阵 Sb实现。

A.卷积神经网络

B.循环神经网络

C.全连接神经网络

D.选项A和B

答案：D

A.L2正则项，作用是最大化分类间隔，使得分类器拥有更强的泛化能力

B.Hinge损失函数，作用是最小化经验分类错误

C.分类间隔为1/||w||，||w||代表向量的模

D.当参数C越小时，分类间隔越大，分类错误越多

答案：C

A正确。考虑加入正则化项的原因：想象一个完美的数据集，y>1是正类，y<-1是负类，决策面y=0，加入一个y=-30的正类噪声样本，那么决策面将会变“歪”很多，分类间隔变小，泛化能力减小。加入正则项之后，对噪声样本的容错能力增强，前面提到的例子里面，决策面就会没那么“歪”了，使得分类间隔变大，提高了泛化能力。

B正确。

C错误。间隔应该是2/||w||才对，后半句应该没错，向量的模通常指的就是其二范数。

D正确。考虑软间隔的时候，C对优化问题的影响就在于把a的范围从[0，+inf]限制到了[0,C]。C越小，那么a就会越小，目标函数拉格朗日函数导数为0可以求出w=求和ai∗yi∗xi，a变小使得w变小，因此间隔2/||w||变大。

A.Dropout

B.分批归一化(Batch Normalization)

C.正则化(regularization)

D.上述选项都可以

答案：D

A.95

B.96

C.97

D.98

答案：C

A.(AB)C

B.AC(B)

C.A(BC)

D.上述所有选项效率相同

答案：A

【解析】首先，根据简单的矩阵知识，因为 A*B， A的列数必须和 B的行数相等。因此，可以排除 B选项，

然后，再看 A、 C选项。在 A选项中，m∗n的矩阵 A和n∗p的矩阵 B的乘积，得到 m∗p的矩阵 A\*B，而 A∗B的每个元素需要 n次乘法和 n-1次加法，忽略加法，共需要 m∗n∗p次乘法运算。同样情况分析 A*B之后再乘以 C时的情况，共需要 m∗p∗q次乘法运算。因此， A选项 (AB)C需要的乘法次数是 m∗n∗p+m∗p∗q。同理分析， C选项 A (BC)需要的乘法次数是 n∗p∗q+m∗n∗q。

A.把除了最后一层外所有的层都冻结，重新训练最后一层

B.对新数据重新训练整个模型

C.只对最后几层进行调参(fine tune)

D.对每一层模型进行评估，选择其中的少数来用

答案：C

【解析】如果有个预先训练好的神经网络,就相当于网络各参数有个很靠谱的先验代替随机初始化.若新的少量数据来自于先前训练数据(或者先前训练数据量很好地描述了数据分布,而新数据采样自完全相同的分布),则冻结前面所有层而重新训练最后一层即可;但一般情况下,新数据分布跟先前训练集分布有所偏差,所以先验网络不足以完全拟合新数据时,可以冻结大部分前层网络,只对最后几层进行训练调参(这也称之为fine tune)。

增加神经网络层数,可能会增加测试数据集的分类错误率

减少神经网络层数,总是能减小测试数据集的分类错误率

增加神经网络层数,总是能减小训练数据集的分类错误率

A. 1

B. 1和 3

C. 1和 2

D. 2

答案：A

【解析】深度神经网络的成功,已经证明增加神经网络层数,可以增加模型范化能力,也就是，训练数据集和测试数据集都表现得更好。但这篇文献中（https://arxiv.org/pdf/1512.03385v1.pdf）,作者提到更多的层,也不一定能保证有更好的表现.所以不能绝对地说层数多的好坏,只能选A

A.分类过程中类别不平衡

B.实例分割过程中，相同类别图像距离过小

C.提取语义信息时，高层语义过少的时候

D.物体定位时，目标面积过小

答案：A

【解析】Focal Loss最初是在[RetinaNet](https://arxiv.org/abs/1708.02002)论文中提出，旨在解决one-stage目标检测中正负样本不均衡的问题，也可扩展到样本的类别不均衡问题上。该损失函数降低了大量简单负样本在训练中所占的权重。

参考自：https://github.com/amusi/daily-question/blob/master/README.md

雕爷学编程MicroPython动手做（07）——零基础学MaixPy之机器视觉

 

机器视觉 machine vision
机器视觉是人工智能正在快速发展的一个分支。机器视觉作为生产过程中关键技术之一，在机器或者生产线上，机器视觉可以检测产品质量以便将不合格的产品剔除，或者指导机器人完成组装工作，与整个生产密切相关。

 

 

什么是机器视觉？
简单来说，机器视觉就是用机器代替人眼来做测量和判断。机器视觉系统是通过机器视觉产品将被摄取目标转换成图像信号，传送给专用的图像处理系统，得到被摄目标的形态信息，根据像素分布和亮度、颜色等信息，转变成数字化信号;图像系统对这些信号进行各种运算来抽取目标的特征，进而根据判别的结果来控制现场的设备动作。机器视觉是一项综合技术，包括图像处理、机械工程技术、控制、电光源照明、光学成像、传感器、模拟与数字视频技术、计算机软硬件技术(图像增强和分析算法、图像卡、 I/O卡等)。一个典型的机器视觉应用系统包括图像捕捉、光源系统、图像数字化模块、数字图像处理模块、智能判断决策模块和机械控制执行模块。

 

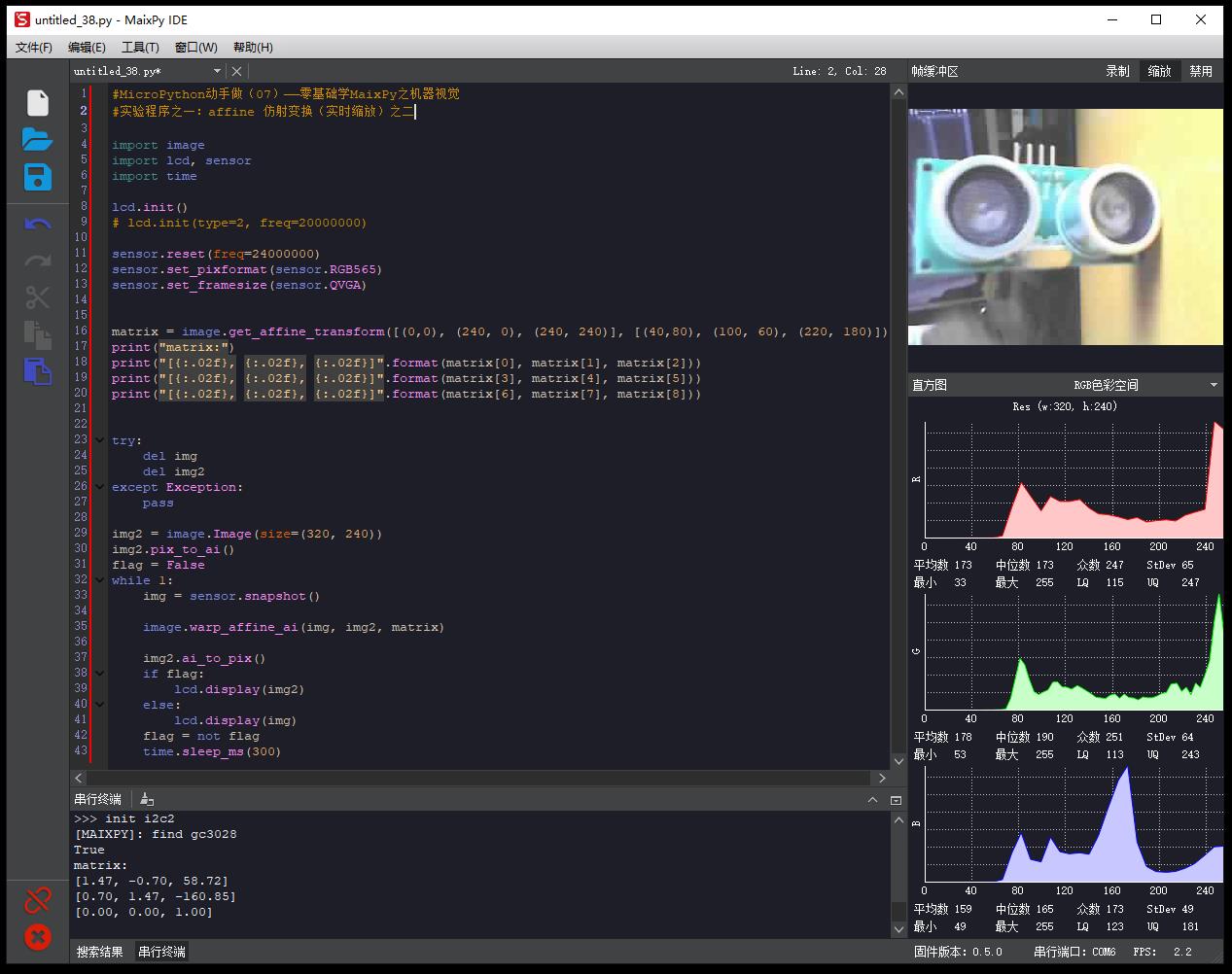
#MicroPython动手做（07）——零基础学MaixPy之机器视觉
#实验程序之一：affine 仿射变换（实时缩放）

 

#MicroPython动手做（07）——零基础学MaixPy之机器视觉
#实验程序之一：affine 仿射变换（实时缩放）

import image
import lcd, sensor
import time

lcd.init()
# lcd.init(type=2, freq=20000000)

sensor.reset(freq=24000000)
sensor.set_pixformat(sensor.RGB565)
sensor.set_framesize(sensor.QVGA)


matrix = image.get_affine_transform([(0,0), (240, 0), (240, 240)], [(60,60), (240, 0), (220, 200)])
print("matrix:")
print("[{:.02f}, {:.02f}, {:.02f}]".format(matrix[0], matrix[1], matrix[2]))
print("[{:.02f}, {:.02f}, {:.02f}]".format(matrix[3], matrix[4], matrix[5]))
print("[{:.02f}, {:.02f}, {:.02f}]".format(matrix[6], matrix[7], matrix[8]))


try:
    del img
    del img2
except Exception:
    pass

img2 = image.Image(size=(320, 240))
img2.pix_to_ai()
flag = False
while 1:
    img = sensor.snapshot()

    image.warp_affine_ai(img, img2, matrix)

    img2.ai_to_pix()
    if flag:
        lcd.display(img2)
    else:
        lcd.display(img)
    flag = not flag
    time.sleep_ms(500)

　　

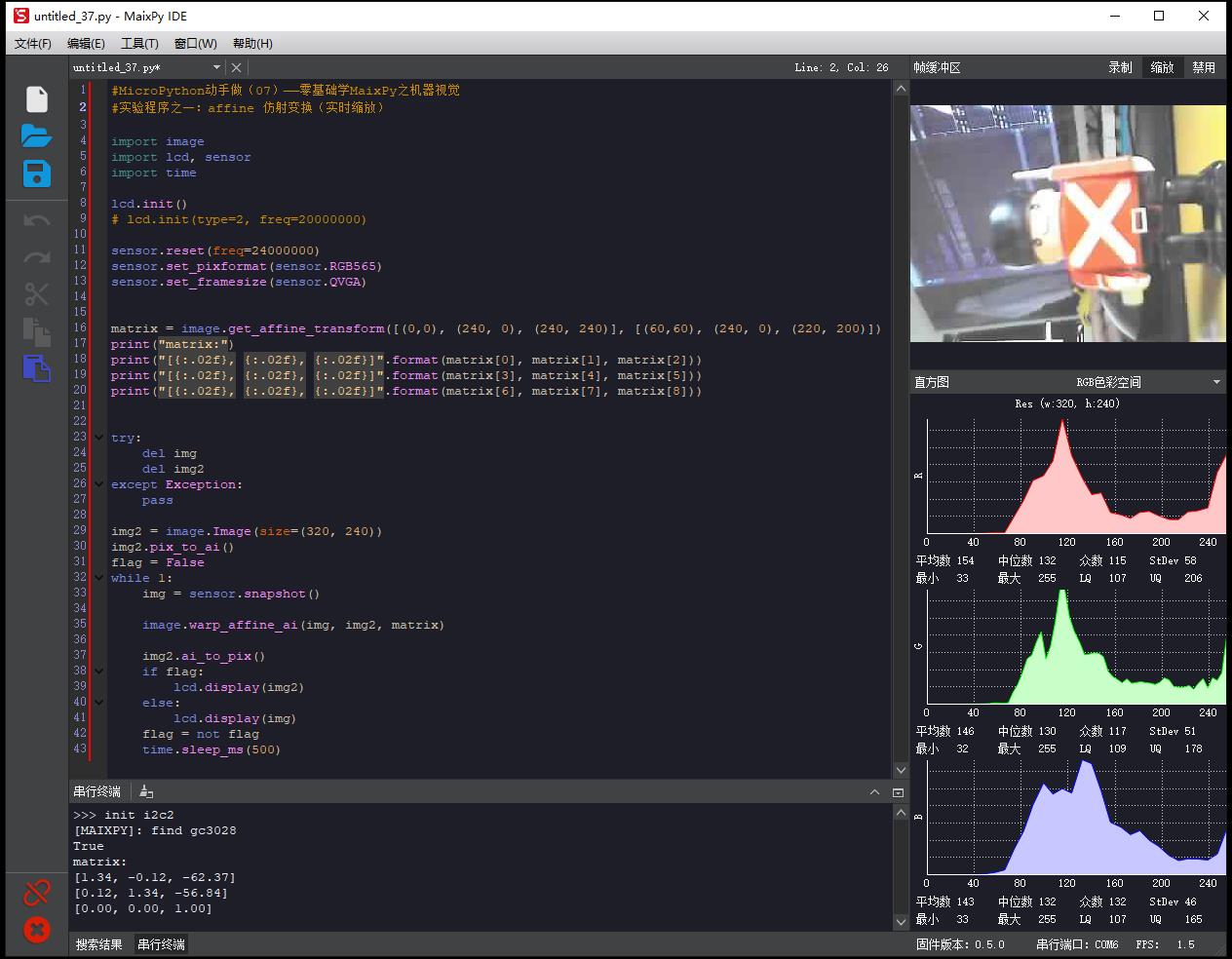
串口输出
>>> init i2c2
[MAIXPY]: find gc3028
True
matrix:
[1.34, -0.12, -62.37]
[0.12, 1.34, -56.84]
[0.00, 0.00, 1.00]

 

变换模型
是指根据待匹配图像与背景图像之间几何畸变的情况，所选择的能最佳拟合两幅图像之间变化的几何变换模型。可采用的变换模型有如下几种:刚性变换、仿射变换、透视变换和非线形变换等，其中第三个的仿射变换就是这里要探讨的。

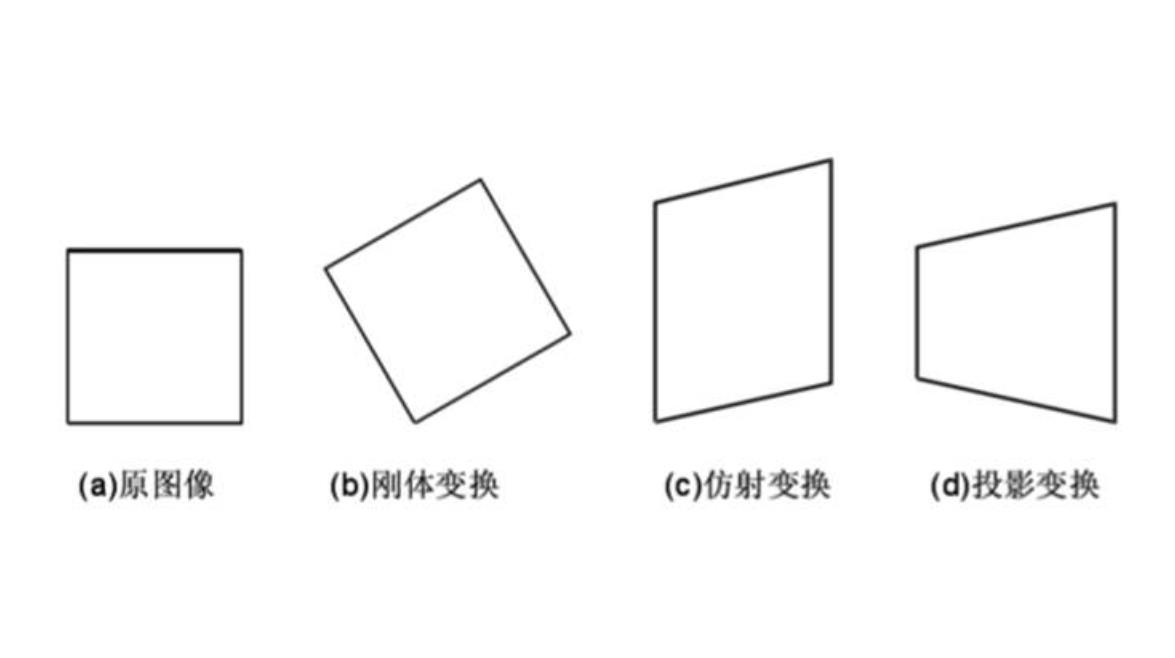
仿射变换
拉伸、收缩、扭曲、旋转是图像的几何变换，在三维视觉技术中大量应用到这些变换，又分为仿射变换和透视变换。仿射变换可以将矩形转换成平行四边形，它可以将矩形的边压扁但必须保持边是平行的，也可以将矩形旋转或者按比例变化。透视变换提供了更大的灵活性，一个透视变换可以将矩阵转变成梯形。当然，平行四边形也是梯形，所以仿射变换是透视变换的子集。

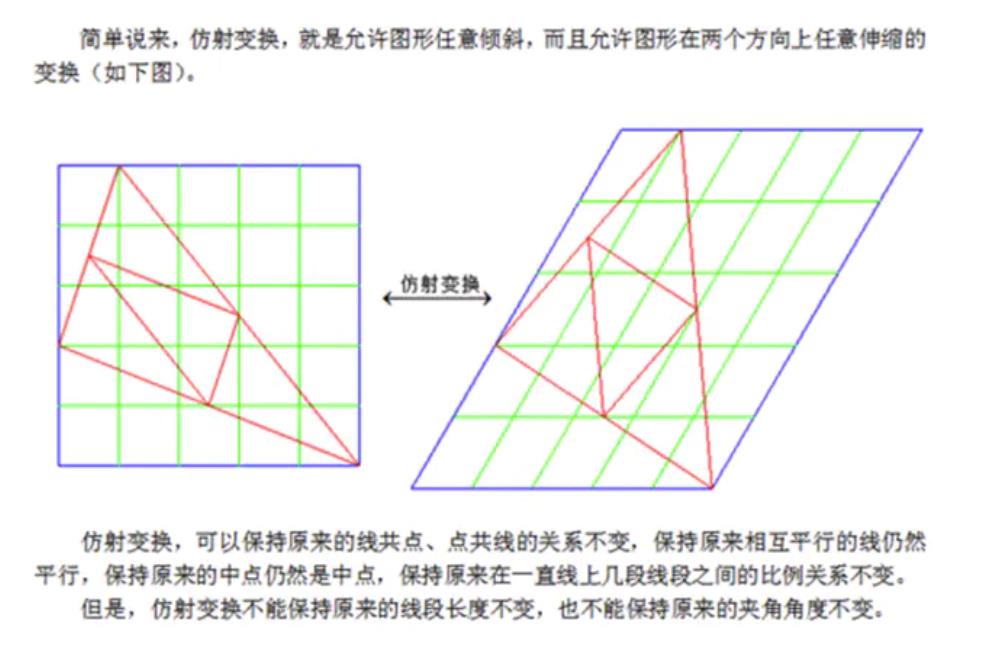
image — 机器视觉

移植于 openmv， 与 openmv 功能相同

get_affine_transform()函数

 

计算3个二维点对之间的仿射变换矩阵H（2行x3列），自由度为6。仿射变换的原理就是根据源图像中一个三角形的顶点坐标和应用仿射变换之后的目标图像中一个三角形的顶点坐标计算出一个变换矩阵，然后将这个矩阵应用到整个源图像。

matrix = image.get_affine_transform([(0,0), (240, 0), (240, 240)], [(60,60), (240, 0), (220, 200)])

　　

前面三组为输入源图像中的三角形顶点坐标

后面三组为输出目标图像中的三角形顶点坐标

 

举例说明

输入源图像中的三角形顶点坐标 ([[20, 20], [30, 20], [20, 0]])

输出目标图像中的三角形顶点坐标 ([[20, 20], [30, 20], [25, 0]])

 

 

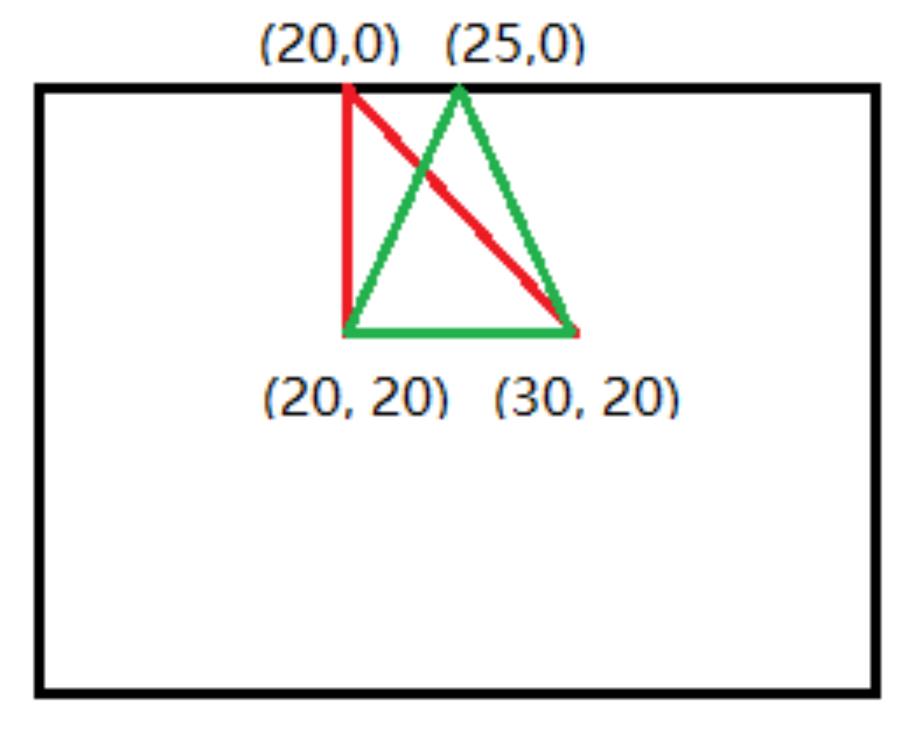
红色是原图中的三角形，绿色是应用仿射变换之后的目标图像的三角形，根据这个设置应用仿射变换之后图像应该像左边扭曲，有了这两个三角形的顶点坐标，get_affine_transform()函数就能计算得到一个仿射变换矩阵，并在原图应用仿射变换就得到了扭曲之后的图像（绿色的）。

 

尝试变动目标图像的三个顶点，看看有什么变化

matrix = image.get_affine_transform([(0,0), (240, 0), (240, 240)], [(60,60), (240, 0), (220, 200)])

matrix = image.get_affine_transform([(0,0), (240, 0), (240, 240)], [(40,80), (100, 60), (220, 180)])

　　

#MicroPython动手做（07）——零基础学MaixPy之机器视觉
#实验程序之一：affine 仿射变换（实时缩放）之二

import image
import lcd, sensor
import time

lcd.init()
# lcd.init(type=2, freq=20000000)

sensor.reset(freq=24000000)
sensor.set_pixformat(sensor.RGB565)
sensor.set_framesize(sensor.QVGA)


matrix = image.get_affine_transform([(0,0), (240, 0), (240, 240)], [(40,80), (100, 60), (220, 180)])
print("matrix:")
print("[{:.02f}, {:.02f}, {:.02f}]".format(matrix[0], matrix[1], matrix[2]))
print("[{:.02f}, {:.02f}, {:.02f}]".format(matrix[3], matrix[4], matrix[5]))
print("[{:.02f}, {:.02f}, {:.02f}]".format(matrix[6], matrix[7], matrix[8]))


try:
    del img
    del img2
except Exception:
    pass

img2 = image.Image(size=(320, 240))
img2.pix_to_ai()
flag = False
while 1:
    img = sensor.snapshot()

    image.warp_affine_ai(img, img2, matrix)

    img2.ai_to_pix()
    if flag:
        lcd.display(img2)
    else:
        lcd.display(img)
    flag = not flag
    time.sleep_ms(300)

　　

 

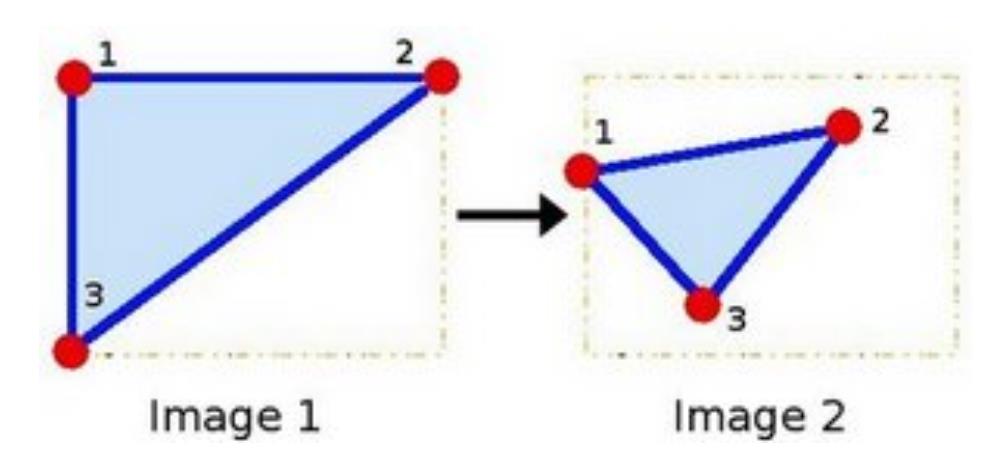
点1, 2 和 3 (在图一中形成一个三角形) 与图二中三个点一一映射, 仍然形成三角形, 但形状已经大大改变. 如果我们能通过这样两组三点求出仿射变换 (你能选择自己喜欢的点), 接下来我们就能把仿射变换应用到图像中所有的点。

 

#MicroPython动手做（07）——零基础学MaixPy之机器视觉
#实验程序之二：image deal 图像处理（深色浮雕）

 

 

#MicroPython动手做（07）——零基础学MaixPy之机器视觉
#实验程序之二：image deal 图像处理（深色浮雕）

import sensor
import image
import lcd
import time

lcd.init(freq=15000000)
sensor.reset()
sensor.set_pixformat(sensor.RGB565)
sensor.set_framesize(sensor.QVGA)
sensor.run(1)
origin = (0,0,0, 0,1,0, 0,0,0)
edge = (-1,-1,-1,-1,8,-1,-1,-1,-1)
sharp = (-1,-1,-1,-1,9,-1,-1,-1,-1)
relievo = (2,0,0,0,-1,0,0,0,-1)

tim = time.time()
while True:
    img=sensor.snapshot()
    img.conv3(edge)
    lcd.display(img)
    if time.time() -tim >10:
        break
tim = time.time()
while True:
    img=sensor.snapshot()
    img.conv3(sharp)
    lcd.display(img)
    if time.time() -tim >10:
        break
tim = time.time()
while True:
    img=sensor.snapshot()
    img.conv3(relievo)
    lcd.display(img)
    if time.time() -tim >10:
        break

lcd.clear()

 

　　

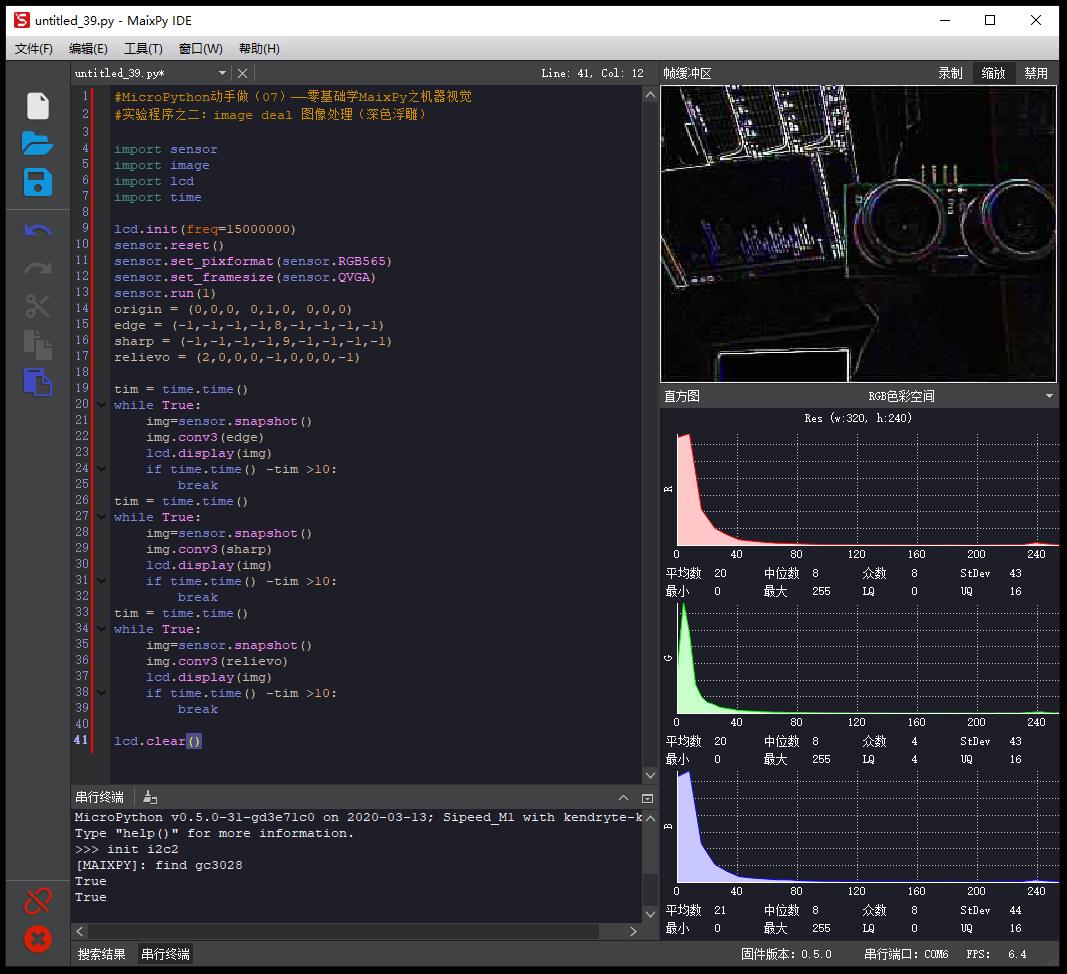
image deal 图像处理
读取图片（或者实时动态摄像），对像素点任意操作并生成图片，如对像素点进行ARGB的分解，或者将ARGB恢复成像素值，对每个像素点进行修改转换等等。
(Read the image, any operation on the pixels to generate the picture. If the pixel of ARGB decomposition or ARGB back into pixel values, modify the conversion, and so each pixel.)