[528]. 按权重随机选择

Posted 2022-10-12 Debroon

[528]. 按权重随机选择

• • 题目
  • 算法设计：加权随机取样

 

---

题目

传送门：528. 按权重随机选择

输入：
["Solution","pickIndex"]
[[[1]],[]]

输出：
[null,0]

解释：
Solution solution = new Solution([1]);
solution.pickIndex(); // 返回 0，因为数组中只有一个元素，所以唯一的选择是返回下标 0。

 

---

算法设计：加权随机取样

加权随机取样，和等概率随机取样不同。

特意制造概率不等的取样，但概率并非任意设定，而是按照定量的权重。

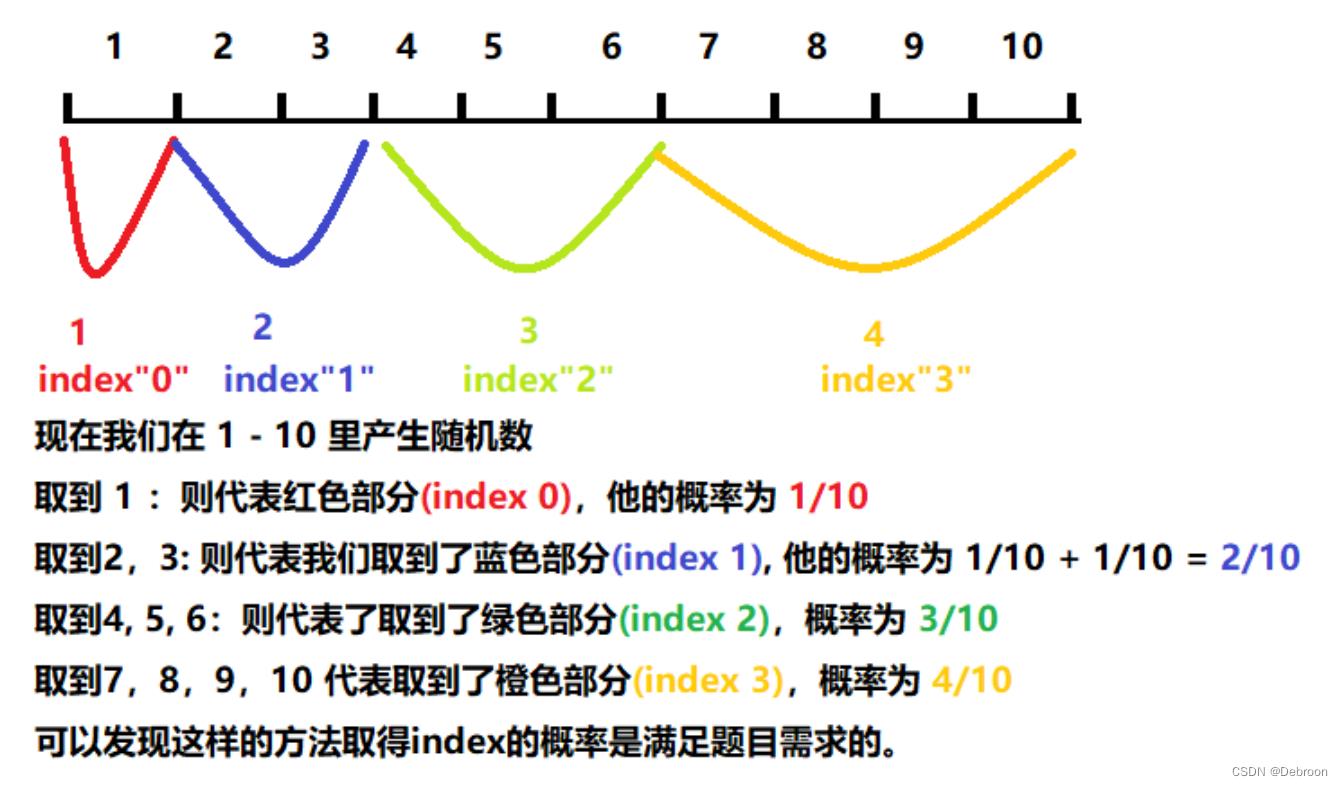
假设我们有数组 w: [1, 2, 3, 4], 那么这个数组的的和为 1 + 2 + 3 + 4 = 10。

对应的我们得到 index 0,1,2,3 的概率为 1/10, 2/10, 3/10, 4/10。‘

数组和为 10，那 rand() % 10 这里产生的数字是 0-9。

我们用数字区间来划分：

• 0 ：取到 index 0，代表概率 1/10
• 1，2: 取到 index 1，代表概率 2/10
• 3，4，5: 取到 index 2，代表概率 3/10
• 6, 7, 8, 9: 取到 index 3，代表概率 4/10

抽象一下：

• 0 ~ w[0]-1 ：取到 index 0，代表概率 1/10
• w[0] ~ w[0] + w[1] - 1: 取到 index 1，代表概率 2/10
• w[0] + w[1] ~ w[0] + w[1] + w[2] - 1: 取到 index 2，代表概率 3/10
• w[0] + w[1] + w[2] ~ w[0] + w[1] + w[2] + w[3] -1： 取到 index 3，代表概率 4/10
• ······
• w[0] + w[1] + ··· + w[n-2] ~ w[0] + w[1] + ··· + w[n-1] - 1：取到 index n-1，代表概率 n/10

图片，好分析一点：

红色框部分，是前缀和。

前缀和的意思是，从位置 0 到位置 i-1 这个区间内的所有的数字之和。

用以上的例子产生的前缀和表 [1, 3, 6, 10], 可以发现我们用得到的数字调用 upper_bound() 会刚好使其指向我们的 index 位置。

upper_bound()：查找大于目标值的第一个元素。

• 0 的 upper_bound 会指向 index 0, 因为第一个比 0 大的数是 w[0] = 1;
• 1, 2 的 upper_bound 会指向 index 1, 因为第一个比 1 或者 2 大的数是 w[1] = 3;
• 3，4，5 的 upper_bound 会指向 index 2, 因为第一个比 3, 4, 5 大的数是 w[2] = 6;
• 6, 7, 8, 9 的 upper_bound 会指向 index 3, 因为第一个比 6，7, 8, 9 大的数是 w[3] = 10;

class Solution 
    vector<int> presum;   // 保存前缀和
public:
    Solution(vector<int>& W) 
        int n = W.size();
        presum.push_back(W[0]); 
        for(int i = 1; i < n; ++i) 
        	presum.push_back(presum.back() + W[i]);
        	// presum.back()：返回数组最后一个元素
    
    
    int pickIndex() 
        int weight = rand() % presum.back();
        return upper_bound(presum.begin(), presum.end(), weight) - presum.begin();
        // upper_bound()：查找大于目标值的第一个元素
        // 满足 presum[i] < 5 且 presum[i] 最大
    
;

时间复杂度：$\theta (logn)$，二分查找实现的 pickIndex()，Solution 类构造函数是 $\theta (n)$

空间复杂度：$\theta (n)$