[470]. 用 Rand7 实现 Rand10

Posted 2022-10-12 Debroon

用 Rand7 实现 Rand10

• • 题目
  • 算法设计：拒绝采样

 

---

题目

 

---

算法设计：拒绝采样

用 Rand7 实现 Rand10。

• Rand10：生成 1 - 10 随机数
• Rand 7：生成 1 - 7 随机数

如果是 用 Rand 10 实现 Rand 7，这样很好实现。

就好像把小卡车的货转到大卡车上，只需要挪一下即可。

调用 Rand 10：

• 如果是 1 - 7，则正常返回
• 如果是 8 - 10，则重新调用 Rand 10，我们把这种思路称为：拒绝采样

那拒绝采样会不会无穷循环？

一般我们算期望，平均情况下需要循环多少次返回结果。

• $E=0.7\ast 1+0.3\ast (1+E)，E是当前这次$

算出来，E = 1.43，计算 1.43 次就可以得到结果。

不会产生无穷循环，在第 4 次的时候概率已经小于 0.1% 了

这就是我们用 Rand 10 实现 Rand 7 的思路 — 拒绝采样。

现在我们不是用大卡车装小卡车的货，而是小卡车装大卡车的货（Rand 7 实现 Rand 10）。

思路依然是拒绝采样，不过我们会使用俩辆小卡车装大卡车的货，确保一定能装下。

即俩个 Rand 7 实现 Rand 10。

调用俩次 Rand 7 的结果会大于 10：

• a = Rand 7 = 1 - 7
• b = Rand 7 = 1 - 7
• c = a + b = 2 - 14

为了能让 c 能生成 1，我们让 a、b 各减一。

• a = Rand 7 - 1 = 0 - 6
• b = Rand 7 - 1 = 0 - 6
• c = a + b = 0 - 12

因为 [0, 12] > [1, 10]，我们就可以采取拒绝采样的思路，多出的部分跳过。

但我们用这种思路生成 [1, 10] 的概率是不相等的。

比如：

• 生成 1 有 2 种，a = 2, b = 1 或者 a = 1，b = 2
• 生成 2 有 3 种，a = 3，b = 1 或者 a = 1，b = 3 或者 a = 2，b = 2

我们需要等概率的方式，一对一的映射。

下图是，俩个 Rand 7 - 1 的组合数：

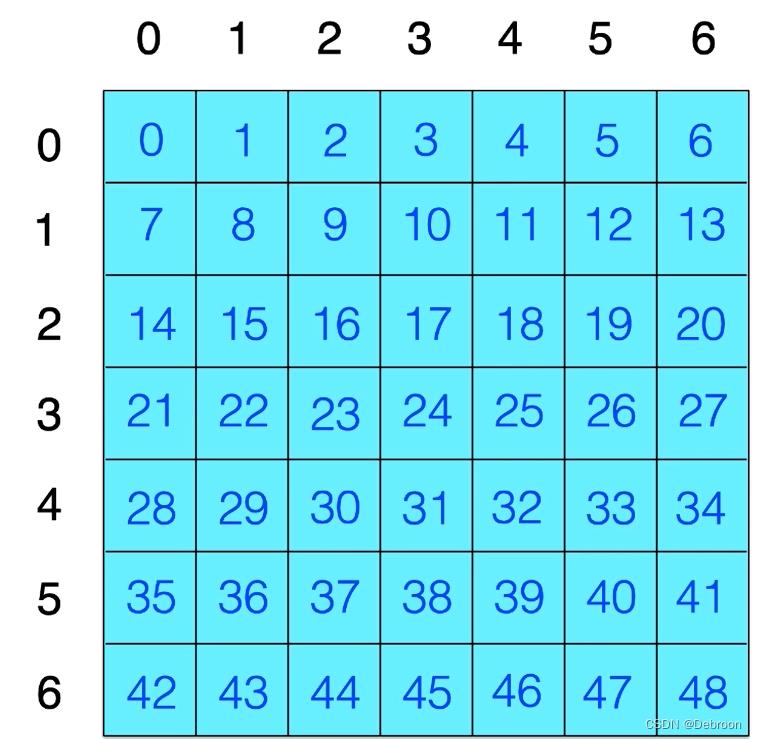
这 49 种结果是等概率出现的。

我们的思路是把，这 49 种结果和 1-10 映射起来。

比如说调用俩次 Rand 7 - 1 的结果 c 是 24。

假设我们要得到二维数组 c[i][j] 在一维数组中的位置：index = i * n + j。

意思就是一共有 i 行,每行 n 个元素，然后再加上第 j 列，也就是有 j 个元素，这样就可以得到一维数组的下标位置。

• 套用二维转一维公式：c = (a - 1) * 7 + (b - 1)。

有了等概率映射，这时我们就可使用拒绝采样啦。

• c = [1, 10] 接受
• c = [11, 49] 拒绝采样

class Solution 
public:
    int rand10() 
        while(true) 
            int num = (rand7() - 1) * 7 + rand7(); 
            // 等概率生成[1,49]范围的随机数
            if( 0 <= num && num <= 10 ) return num; 
            // 拒绝采样，并返回[1,10]范围的随机数
        
    
;

不过这个拒绝采样的概率太了大吧。

为了降低对 rand7 的调用次数，减少无效的拒绝采样次数。

范围 [0, 48] 中，只有 [1,10] 范围内的数据会被接受返回，其余情况均被拒绝重试。

为了尽可能少的调用 rand7 方法，我们可以从 [0, 48] 中取与 [1,10] 成倍数关系的数，来进行转换。

我们可以取 [0, 48] 中的 [1, 40] 范围内的数来代指 [1, 10]。

首先在 [0, 48] 中取 [1, 40] 仍为等概率，其次形如 x1 的数值有 44 个（1、11、21、31），形如 x2 的数值有 4 个（2、12、22、32）… 因此最终结果仍为等概率。

• c = [11，40] 接受
• c = [41，49] 拒绝采样

class Solution 
public:
    int rand10() 
        while(true) 
            int num = (rand7() - 1) * 7 + rand7(); 
            // 等概率生成[1,49]范围的随机数
            if(num <= 40) return num % 10 + 1; 
            // 拒绝采样，并返回[1,10]范围的随机数
        
    
;

时间复杂度：$\theta (1)$

空间复杂度：$\theta (1)$