梯度的方向与等高线切线方向垂直

Posted 2022-10-07 哦...

方向导数和梯度的概念已经不用赘述：

方向导数是函数z在某个具体点上（例如(x0,y0,z0...)）沿通过该点的射线L方向计算得到的导数。

方向导数写成向量相乘的方式时，就是梯度乘以与L同方向的单位向量。

当单位向量的方向与梯度向量方向一致时（也就是单位向量与梯度向量的夹角θ为0°角时），z函数在某点L方向的方向导数达到最大值，最大值就是梯度的值（模）。

这里一直隐含了一个东西，梯度也是向量（由z函数在某具体点对各个变量求偏导组成）它也是有方向的，当L射线与此时梯度方向一致时，方向导数达到最大值，也就是梯度的模。换句话说，在某个具体点上，梯度方向永远是函数上升最陡峭的方向，但是梯度的方向该如何计算呢？

以下内容转自[知乎]为什么梯度的方向与等高线切线方向垂直？

 

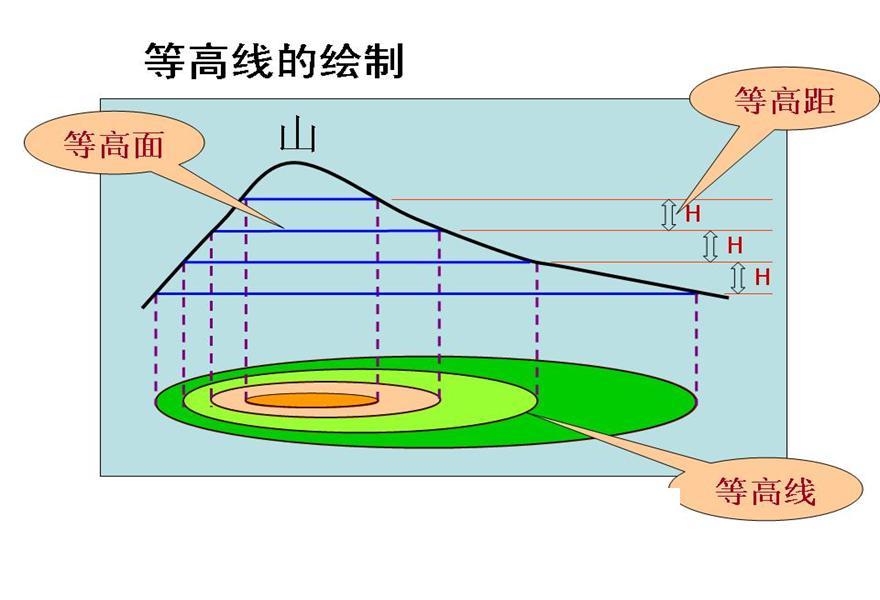
在三维曲面上的梯度更新过程中，很多地方出现梯度的下降方向是如下这样走的：

图片来源于百度百科。从图上能够看出，梯度下降的方向与等高线的切线方向垂直。

那么为什么会垂直呢？其实是一个高数问题。

解释

假设我们的损失函数为z=f(x,y)，在几何上表示是一个曲面，该曲面被平面c（c为常数）所截得的曲线l方程为：

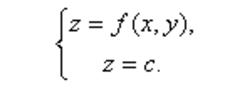
这条曲线l在xy轴平面上的投影是一条平面曲线Q，它在xy平面直角坐标系中的方程为

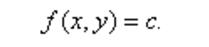
则我们称平面曲线Q为函数z=f(x,y)的等高线。

由于等高线f(x,y)=c上任意一点的切线斜率为dy/dx，则等高线f(x,y)=c上任意一点(x,y)处的法线的斜率为：

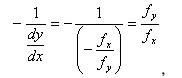
又因为梯度的计算式子为：

则可以得到梯度的方向为：

从上可以看出梯度的方向与等高线f(x,y)=c上任意一点的法线斜率是相同的。

这也就解释了为什么梯度的方向与等高线切线方向垂直的原因。结论如下：

函数z=f(x,y)在点p(x,y)的梯度的方向与过点p的等高线f(x,y)=c在这点的法线一个方向相同。梯度的方向与等高线切线方向垂直。