从寻找谷神星的过程，谈最小二乘法实现多项式拟合
Posted 天元浪子
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了从寻找谷神星的过程，谈最小二乘法实现多项式拟合相关的知识，希望对你有一定的参考价值。
科学史上众星云集，璨若星河。这些牛人基本上都是天才，但也不乏无名之辈凭借匪夷所思、骇世惊俗的猜想而跻身于巨星之列。比如，门捷列夫，整了一张留空的元素周期表，引得全世界的化学家去做填空题。还有一位德国的中学老师，名唤约翰·提丢斯（Johann Daniel Titius）的，在1766年写下了这么一个数列：
(0+4)/10 = 0.4
(3+4)/10 = 0.7
(6+4)/10 = 1.0
(12+4)/10 = 1.6
(24+4)/10 = 2.8
(48+4)/10 = 5.2
(96+4)/10 = 10.0
(192+4)/10 = 19.6
(384+4)/10 = 38.8
...
当时，人们已知太阳系有六大行星，即水星、金星、地球、火星、木星、土星。如果以日地距离（约1.5亿公里）为一个天文单位，则六大行星距离太阳的距离，恰好接近提丢斯的这个数列，并且留下了无限的遐想！这个数列被称为提丢斯——波得定则。
1781年，英籍德国人赫歇尔在接近19.6的位置上（即数列中的第八项）发现了天王星，从此，人们就对这一定则深信不疑了。根据这一定则，在数列的第五项即2.8的位置上也应该对应一颗行星，只是还没有被发现。于是，许多天文学家和天文爱好者便以极大的热情，踏上了寻找这颗新行星的征程。
1801年新年的晚上，意大利神父朱塞普·皮亚齐还在聚精会神地观察着星空。突然，他从望远镜里发现了一颗非常小的星星，正好在提丢斯——波得定则中2.8的位置上。这颗行星在几天的观测期内不断变动位置。当皮亚齐再想进一步观察这颗小行星时，他却病倒了。等到他恢复健康，再想寻找这颗小行星时，它却不知所踪。皮亚齐没有放弃这一机会，他认为这可能就是人们一直没有发现的那颗行星。
天文学家对皮亚齐的这一发现持有不同的看法。有人认为皮亚齐是正确的，也有人认为这可能是一颗彗星，关于这颗行星的说法不在少数，天文学界议论纷纷。
此时，又一位大神出现了，他就是数学天才高斯。根据皮亚齐的观测资料，高斯以其卓越的数学才能，只用了一个小时就算出了这颗神秘小行星的轨道形状，并指出它将于何时出现在哪一片天空里。1801年12月31日夜，德国天文爱好者奥伯斯，在高斯预言的时间里，用望远镜对准了这片天空。不出所料，这颗神秘小行星再一次奇迹般地出现了！
从约翰·提丢斯，到神父朱塞普·皮亚齐，再到数学王子高斯、天文爱好者奥伯斯，众多牛人联手发现的这个天体，被命名为谷神星。谷神星是太阳系中最小的、也是唯一位于小行星带的矮行星。谷神星曾经被当作一个标准：凡是比它大的行星，可以视为和地球平级的行星，否则视为小行星。比如冥王星，比谷神星大，被封为太阳系的老九，直到2006年，因为被分类到矮行星，才退出了九大行星的行列。
那么，高斯究竟是如何计算谷神星运行轨道并作出预测的呢？其实就是使用最小二乘法拟合轨迹线。高斯使用的最小二乘法发表于1809年他的著作《天体运动论》中。
让我们冒充高斯，来一次cosplay，体会一下做牛人的感觉吧。
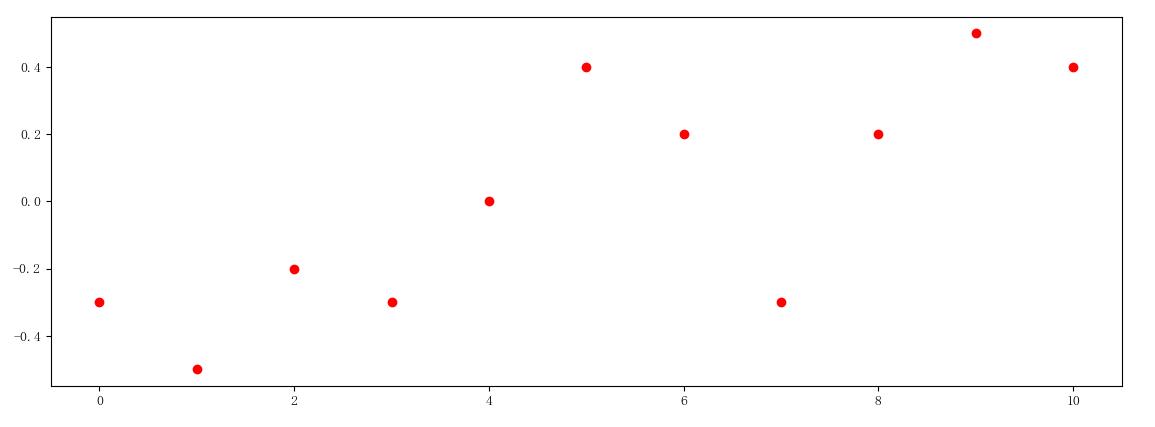假定上图是皮亚齐从零时到十时的谷神星观测记录，每一个红点对应的横坐标表示观测时间，对应的纵坐标表示谷神星的位置。如果有一条曲线（非常接近地）经过了上图的11个观测点，只要找到这条曲线的方程：
y = f ( x ) y = f(x) y=f(x)
我们就可以随意预测11时、12时的谷神星位置了。当年高斯就是这么想的。可是，如何找到这条曲线的方程呢？这个问题难不住高斯。他用一个k次多项式
g
(
x
)
g(x)
g(x) 来近似
f
(
x
)
f(x)
f(x)：
f
(
x
)
≈
g
(
x
)
=
a
0
+
a
1
x
+
a
2
x
2
+
a
3
x
3
+
.
.
.
+
a
k
x
k
f(x) \\approx g(x) = a_0 + a_1x + a_2x^2 + a_3x^3 + ... + a_kx^k
f(x)≈g(x)=a0+a1x+a2x2+a3x3+...+akxk
通过选择合适的系数
a
0
,
a
1
,
a
2
,
a
3
,
.
.
.
,
a
k
a_0,a_1,a_2,a_3,...,a_k
a0,a1,a2,a3,...,ak，令误差：
l
o
s
s
=
∑
i
=
0
10
(
g
(
i
)
−
f
(
i
)
)
2
loss = \\sum_i=0^10(g(i)-f(i))^2
loss=i=0∑10(g(i)−f(i))2
为最小，就可以认为
g
(
x
)
g(x)
g(x) 就是我们要寻找的曲线方程了。高斯的最小二乘法，就是根据观测数据和给定的多项式次数
k
k
k 来寻找误差最小的一组多项式系数
a
0
,
a
1
,
a
2
,
a
3
,
.
.
.
,
a
k
a_0,a_1,a_2,a_3,...,a_k
a0,a1,a2,a3,...,ak，有了这组系数，就可以得到
g
(
x
)
g(x)
g(x)，进而计算出
g
(
11
)
g(11)
g(11) 、
g
(
12
)
g(12)
g(12) 的值 ，这样就可以预测谷神星在11时、12时的位置了。
我们不是高斯，不会使用最小二乘法，幸好 numpy 给我们提供了强大的工具，使得我们可以继续冒充高斯。
>>> import numpy as np
>>> _x = np.linspace(0, 10, 11)
>>> _y = np.array([-0.3, -0.5, -0.2, -0.3, 0, 0.4, 0.2, -0.3, 0.2, 0.5, 0.4])
>>> np.polyfit(_x, _y, 3)
array([ 0.00066045, -0.01072261, 0.12684538, -0.43146853])
这里，_x 是皮亚齐的观测时间序列，_y 是皮亚齐观测到的谷神星位置序列，我们选择多项式次数为3。执行np.polyfit(xs, ys, 3)，就是用最小二乘法找到三次多项式的4个系数，使得这个三次多项式和观测数据的误差最小。这个三次多项式写出来是这样的：
g ( x ) = − 0.43146853 + 0.12684538 x − 0.01072261 x 2 + 0.00066045 x 3 g(x) = -0.43146853 + 0.12684538x - 0.01072261x^2 + 0.00066045x^3 g(x)=−0.43146853+0.12684538x−0.01072261x2+0.00066045x3
用这个函数去验证观测数据：
>>> g = np.poly1d(np.polyfit(_x, _y, 3))
>>> g(_x)
array([-0.43146853, -0.31468531, -0.21538462, -0.12960373, -0.05337995,
0.01724942, 0.08624709, 0.15757576, 0.23519814, 0.32307692,
0.42517483])
>>> loss = np.sum(np.square(g(_x)-_y))
>>> loss
0.4857342657342658
>>> import matplotlib.pyplot as plt
>>> plt.plot(_x, _y, c='r', ls='', marker='o')
>>> plt.plot(_x, g(_x), c='g', ls=':')
>>> plt.show()
用三次多项式 g ( x ) g(x) g(x) 代替 f ( x ) f(x) f(x)，最小误差是0.4857。 观测数据和 g ( x ) g(x) g(x) 的近似数据画在一起，效果如下
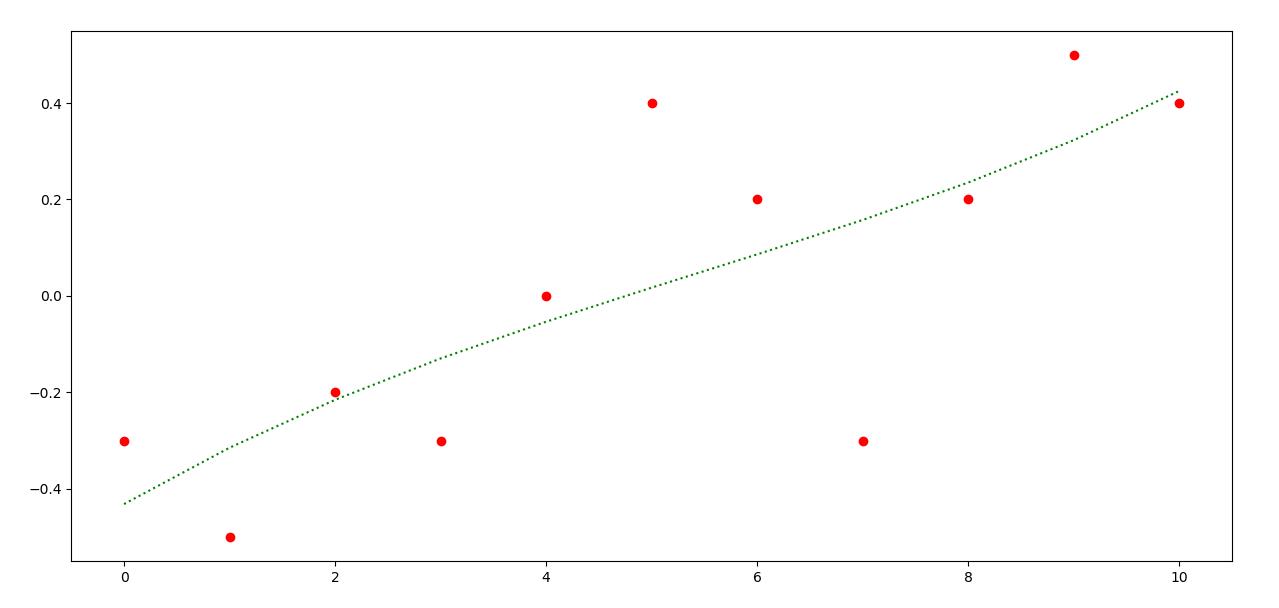很显然，这个拟合效果是无法找到谷神星的。别着急，我们还可以尝试更高次幂的多项式，看看效果如何。下面的代码，同时画出了4至9次多项式的拟合结果和误差。
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['FangSong']
plt.rcParams['axes.unicode_minus'] = False
_x = np.linspace(0, 10, 11)
_y = np.array([-0.3, -0.5, -0.2, -0.3, 0, 0.4, 0.2, -0.3, 0.2, 0.5, 0.4])
g3 = np.poly1d(np.polyfit(_x, _y, 3))
g4 = np.poly1d(np.polyfit(_x, _y, 4))
g5 = np.poly1d(np.polyfit(_x, _y, 5))
g6 = np.poly1d(np.polyfit(_x, _y, 6))
g7 = np.poly1d(np.polyfit(_x, _y, 7))
g8 = np.poly1d(np.polyfit(_x, _y, 8))
g9 = np.poly1d(np.polyfit(_x, _y, 9))
loss3 = np.sum(np.square(g3(_x)-_y))
loss4 = np.sum(np.square(g4(_x)-_y))
loss5 = np.sum(np.square(g5(_x)-_y))
loss6 = np.sum(np.square(g6(_x)-_y))
loss7 = np.sum(np.square(g7(_x)-_y))
loss8 = np.sum(np.square(g8(_x)-_y))
loss9 = np.sum(np.square(g9(_x)-_y))
plt.plot(_x, _y, c='r', ls='', marker='o')
plt.plot(_x, g3(_x), label=u'三次多项式，误差%0.4f'%loss3)
plt.plot(_x, g4(_x), label=u'四次多项式，误差%0.4f'%loss4)
plt.plot(_x, g5(_x), label=u'五次多项式，误差%0.4f'%loss5)
plt.plot(_x, g6(_x), label=u'六次多项式，误差%0.4f'%loss6)
plt.plot(_x, g7(_x), label=u'七次多项式，误差%0.4f'%loss7)
plt.plot(_x, g8(_x), label=u'八次多项式，误差%0.4f'%loss8)
plt.plot(_x, g9(_x), label=u'九次多项式，误差%0.4f'%loss9)
plt.legend()
plt.show()
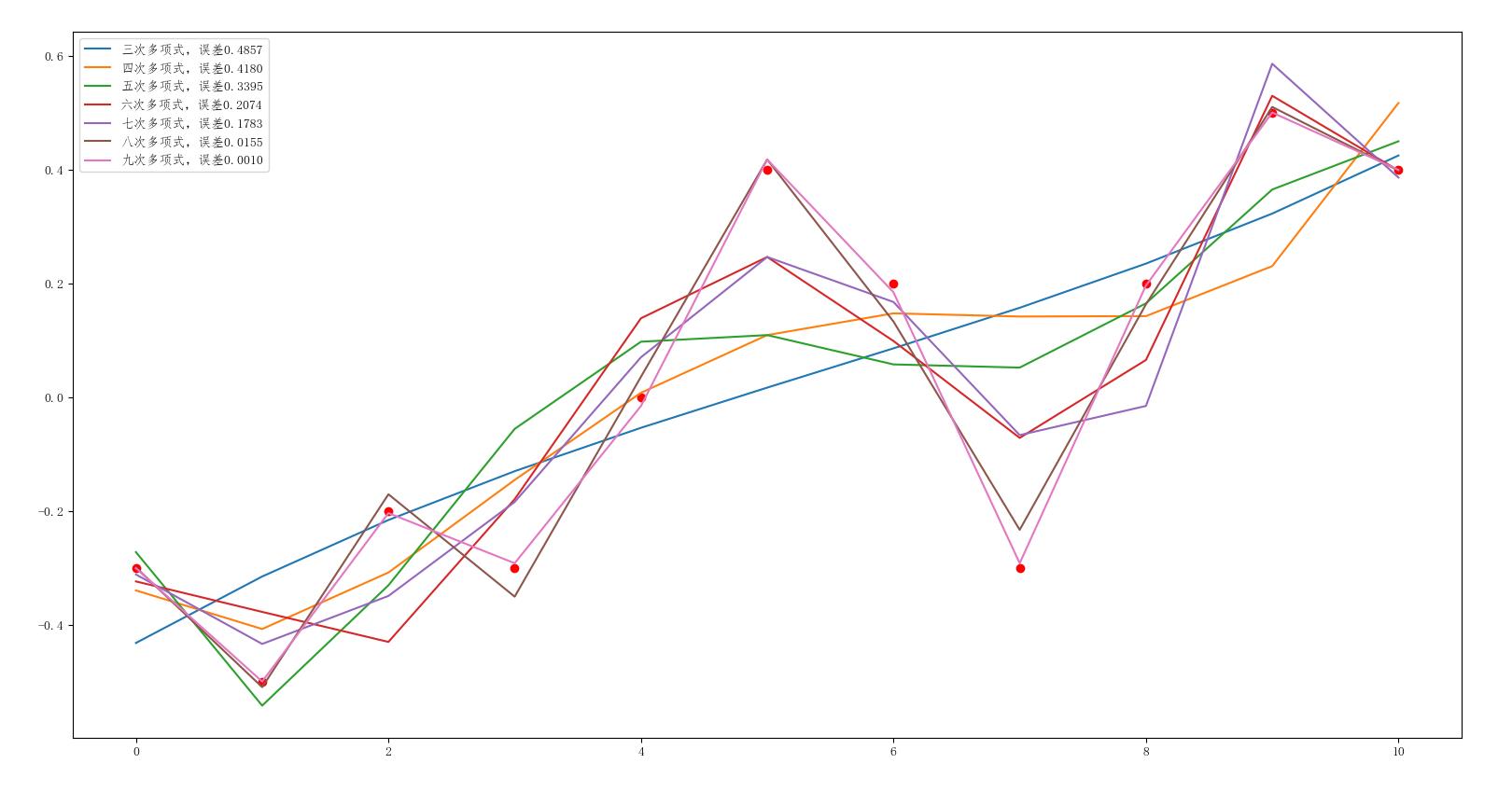可以看到9次多项式拟合的误差，已经小到了0.0010，拟合曲线近乎精准地经过了所有的观测点。这个效果足可令人满意。下图只保留了9次多项式的拟合结果，看起来更清晰。
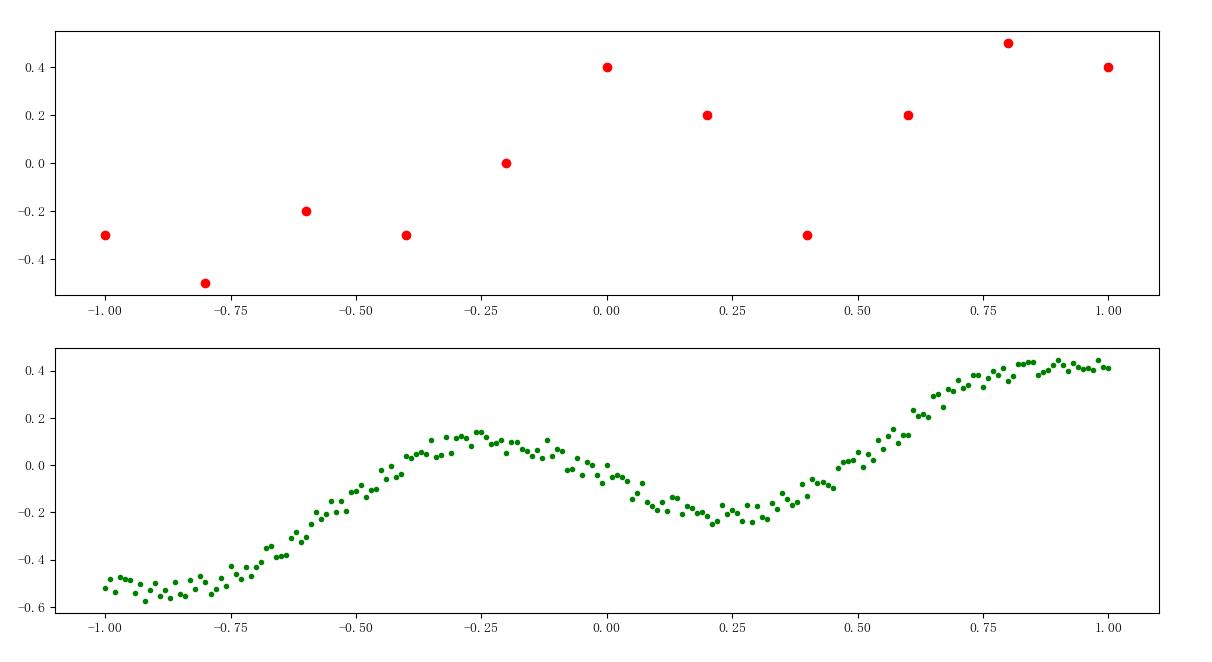
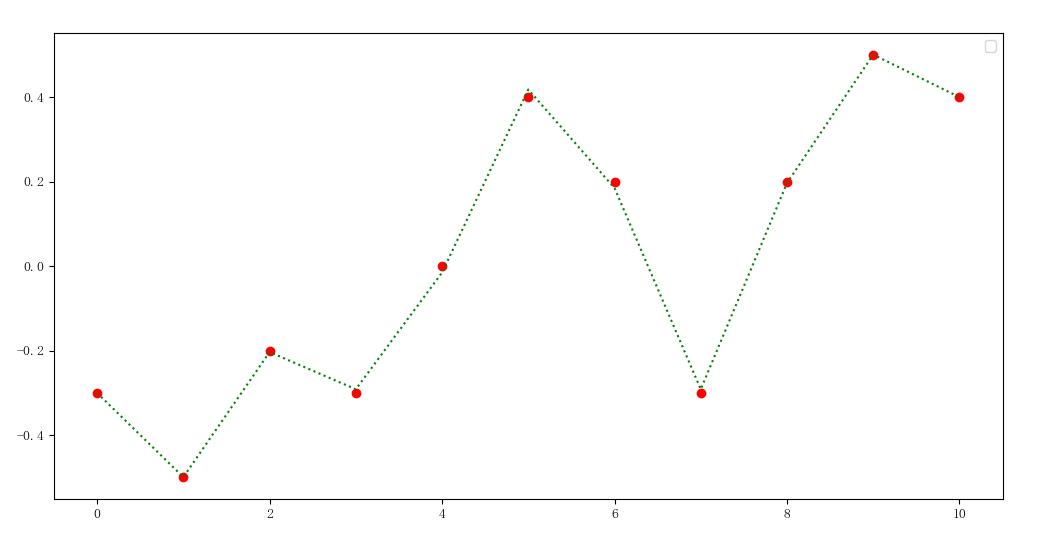Well, cosplay is over. 真正的天体运行轨道不会这么变态，天体位置也不是一个单值就可以表示出来的。上面的例子，纯粹就是多项式拟合。有时候，待拟合数据是下图所示的样子，没关系，上面的拟合方法仍然是有效的。
拟合代码如下：
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['FangSong']
plt.rcParams['axes.unicode_minus'] = False
xs = np.linspace(-1, 1, 11)
ys = np.array([-0.3, -0.5, -0.2, -0.3, 0, 0.4, 0.2, -0.3, 0.2, 0.5, 0.4])
xm = np.linspace(-1, 1, 201)
ym = ((xm**2-1)**3 + 0.5)*np.sin(2*xm) + np.random.random(201)/10 - 0.1
fs4 = np.poly1d(np.polyfit(xs, ys, 4))
fs5 = np.poly1d(np.polyfit(xs, ys, 5))
fs6 = np.poly1d(np.polyfit(xs, ys, 6))
fs7 = np.poly1d(np.polyfit(xs, ys, 7))
fs8 = np.poly1d(np.polyfit(xs, ys, 8))
fs9 = np.poly1d(np.polyfit(xs以上是关于从寻找谷神星的过程，谈最小二乘法实现多项式拟合的主要内容，如果未能解决你的问题，请参考以下文章