最优化简介-第一节:最优化问题概括
Posted 快乐江湖
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了最优化简介-第一节:最优化问题概括相关的知识,希望对你有一定的参考价值。
文章目录
一:最优化问题的一般形式
最优化问题的一般形式:可以描述为如下,理解为在 x ∈ χ x\\in \\chi x∈χ的约束下,最小化(当然最大化就是 m a x max max)问题 f ( x ) f(x) f(x)
m i n f ( x ) , s . t . x ∈ χ ① min\\quad f(x), \\quad s.t.\\quad x\\in \\chi\\quad \\quad① minf(x),s.t.x∈χ①
注意:
-
x x x= ( x 1 , x 2 , . . . , x n ) T ∈ R n (x_1,x_2,...,x_n)^T\\in \\R^n (x1,x2,...,xn)T∈Rn是决策变量
-
f f f: R n → R \\R^n\\rightarrow \\R Rn→R是目标函数
-
χ ⊆ R n \\chi \\subseteq \\R_^n χ⊆Rn是可行域;可行域包含的点称之为可行解;当 χ = R n \\chi =\\R^n χ=Rn时,此时称为无约束优化问题
-
集合 χ \\chi χ通常可以由约束函数 c i ( x ) c_i(x) ci(x): R n → R \\R^n\\rightarrow \\R Rn→R, i = 1 , 2 , . . . , m + l i=1,2,...,m+l i=1,2,...,m+l表达为如下形式
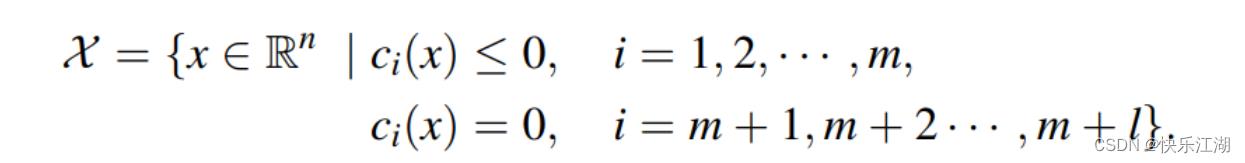
-
在所有满足约束条件的决策变量中,使目标函数取最小值的变量 x ∗ x^* x∗称为优化问题①的最优解,即对任意 x ∈ χ x\\in \\chi x∈χ都有 f ( x ) ≥ f ( x ∗ ) f(x)\\geq f(x^*) f(x)≥f(x∗)
-
如果在集合 χ \\chi χ上,函数 f f f的最小或最大值不存在,则可以关心其下界或上界,也即 i n f f inf\\quad f inff或 s u p f sup\\quad f supf
因此,总的来说,最优化问题主要涉及以下三个要素
- 决策变量 x x x= ( x 1 , x 2 , . . . , x n ) T ∈ R n (x_1,x_2,...,x_n)^T\\in \\R^n (x1,x2,...,xn)T∈Rn:表示我们在最优化问题中要求解的变量
- 目标函数 f f f( R n → R \\R^n\\rightarrow \\R Rn→R):表示我们需要最大化或最小化的表达式
- 约束函数 c i c_i ci( R n → R \\R^n\\rightarrow \\R Rn→R):表示我们需要满足的等式或不等式条件
比如下面的最优化问题
- 决策变量 x ∈ R x\\in \\R x∈R
- 目标函数 f ( x ) = 1 2 ( x − 1 ) 2 + 1 f(x)=\\frac12(x-1)^2+1 f(x)=21(x−1)2+1
- 约束条件
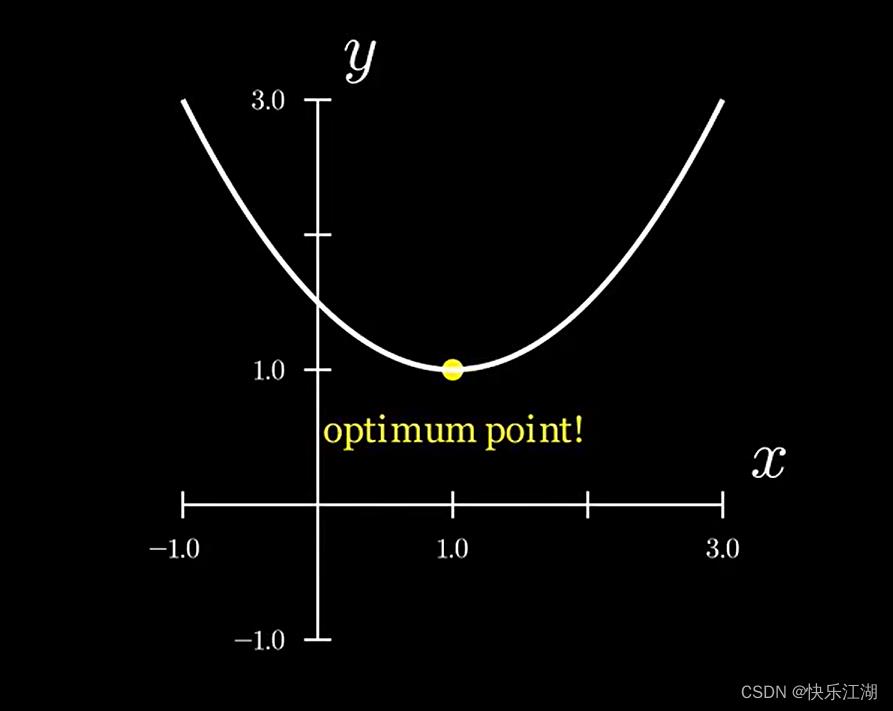
m i n x ∈ R 1 2 ( x − 1 ) 2 + 1 \\mathopmin\\limits_x\\in R\\frac12(x-1)^2+1 x∈Rmin21(x−1)2+1
这个问题,只需画出该函数图像便可解决
二:一个简单例子
如下是一个男女双方相互匹配相亲的例子,双方两两匹配,故可以形成一个匹配矩阵,其中每个元素为 c i j c_ij cij,表示男生 i i i和女生 j j j的匹配度
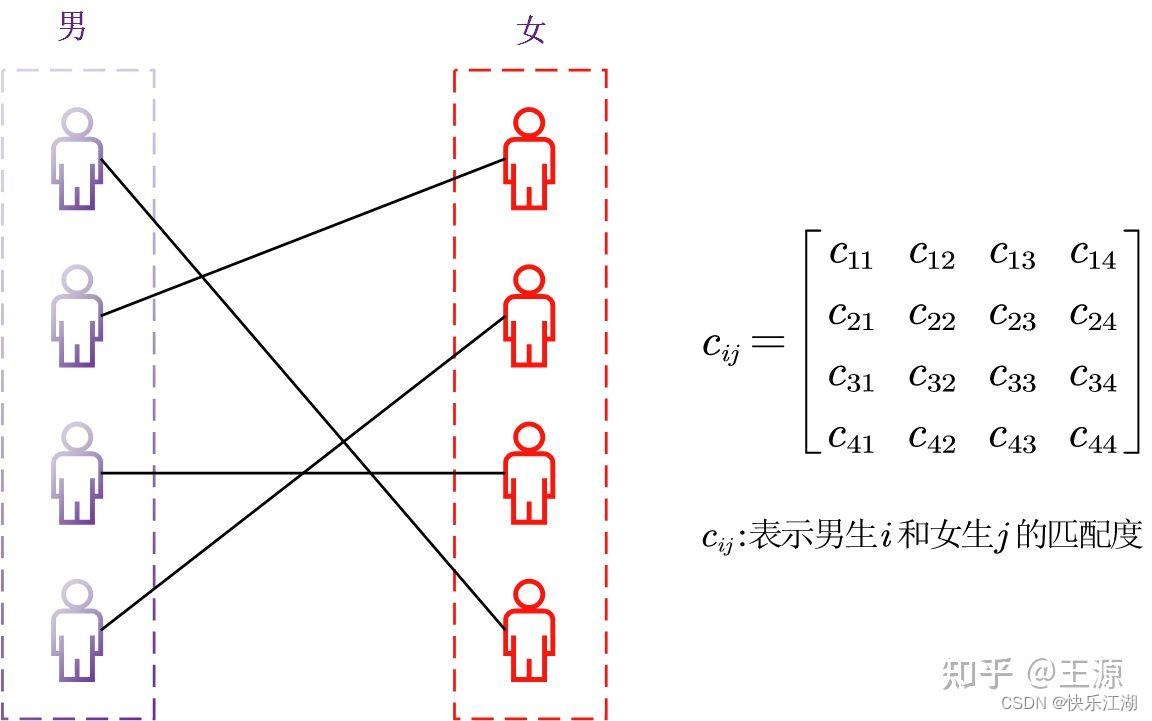
为了使相亲结果更好就要使总的匹配度高,所以这时一个可以用最优化来解决的问题
首先定义决策变量 x i j x_ij xij,取值及相应含义如下
| x i j x_ij xij | 含义 |
|---|---|
| 1 | 男生 i i i和女生 j j j匹配 |
| 0 | 男生 i i i和女生 j j j不匹配 |
假设有 N N N位男生和 N N N位女生,那么该优化问题可以描述为
m a x ∑ i = 1 N ∑ j = 1 N c i j x i j max\\sum\\limits_i=1^N\\sum\\limits_j=1^Nc_ijx_ij maxi=1∑Nj=1∑Ncijxij
s . t . s.t. s.t.
- ∑ i = 1 N x i j = 1 , ∀ j = 1 , 2 , . . . , N \\sum\\limits_i=1^Nx_ij=1, \\quad \\forall j=1,2,...,N \\quad i=1∑Nxij=1,∀j=1,2,...,N:限制一个男生匹配一个女生
- ∑ j = 1 N x i j = 1 , ∀ i = 1 , 2 , . . . , N \\sum\\limits_j=1^Nx_ij=1, \\quad \\forall i=1,2,...,N \\quad j=1∑Nxij=1,∀i=1,2,...,N:限制一个女生匹配一个男生
三:最优化问题分类
(1)有约束和无约束
无约束
m i n x ∈ R 1 2 ( x − 1 ) 2 + 1 \\mathopmin\\limits_x\\in R\\frac12(x-1)^2+1 x∈Rmin2