一文带你读懂，这三个交换机层级的区别和联系。

Posted 2023-04-05 GLAB-Mary

01 第二层交换机

OSI参考模型的第二层叫做数据链路层，第二层交换机通过链路层中的MAC地址实现不同端口间的数据交换。

第二层交换机主要功能，就包括物理编址、错误校验、帧序列以及数据流控制。

因为这是最基本的交换技术产品，目前桌面型交换机一般是属于这类型，所以一般来说，桌面型交换机所承担的工作复杂性不是很强，又处于网络的最基层，所以也就只需要提供最基本的数据链接功能即可。

第二层交换机的应用是最为普遍的，一般应用于局域网的接入层，用来连接用户的计算机，并且其价格便宜，功能符合中、小企业实际应用需求。

通过二层交换机，你可以轻松地将位于同一VLAN内的数据帧从源端发送到目的端，而无需物理连接或位于同一位置。

因此，软件公司的服务器可以集中放置在一个位置，而分散在其他位置的客户端可以轻松访问数据而没有延迟，从而节省服务器成本和时间。

组织可以通过使用这些类型的交换机将主机配置在同一个VLAN中，而不需要任何互联网连接，从而实现内部通信。

总结一下二层交换机的特点：

1. 二层交换机可以充当网桥，将计算机网络系统的各种终端设备连接在一个平台上。它们能够非常快速且有效地将数据从LAN 网络的源端传输到目标端。

2. 二层交换机通过从交换机的地址表中学习目的节点的MAC地址，执行交换功能，将数据帧从源端重新排列到目的端。

3. MAC地址表为二层设备提供了唯一的地址，用于标识数据下发的终端设备和节点。

4. 二层交换机将庞大复杂的 LAN 网络拆分为一个个小的VLAN网络。

5. 通过在一个大型的 LAN 网络中配置多个 VLAN，在没有物理连接的情况下，交换变得更快。

02 第三层交换机

OSI参考模型的第三层叫做网络层，第三层交换机可以看成是路由器和二层交换机的结合，它比第二层交换机更加高档，功能更强。

它们比二层交换机具有更快的切换速度，甚至比传统路由器更快，因为它们不使用额外的跃点来执行数据包的路由，从而会带来更好的性能。

它通常在数据链路层进行交换，仅在需要时（如VLAN间的通信）才在网络层进行路由。

第三层交换机利用网络层的数据包头部信息来增强第二层交换机的功能，依据IP地址信息提供给网络路径选择，并实现不同网段间的数据交换。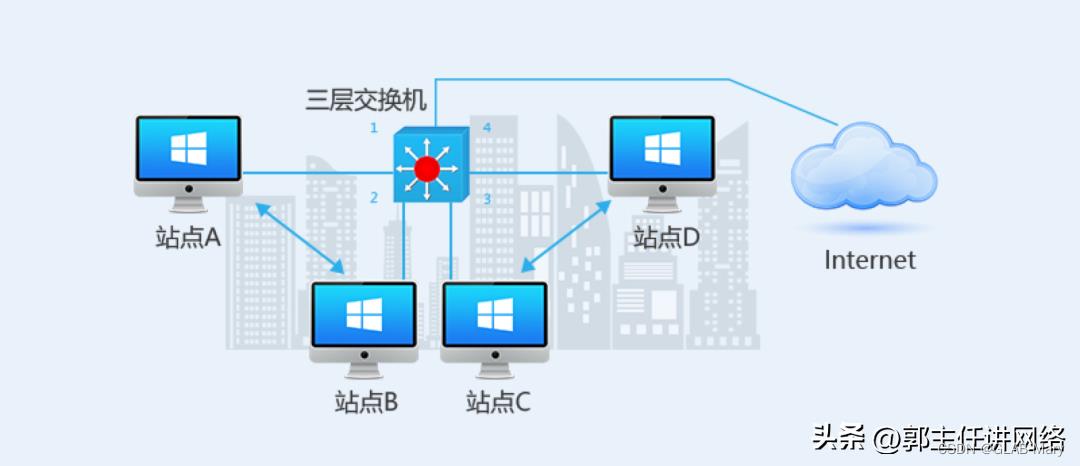

第三层交换机可以隔离广播域，具有很高的数据转发能力和良好的路由控制能力，能够实现不同VLAN主机间的高速路由。

当网络规模较大的时候，你就可以根据特殊应用需求划分为小面独立的VLAN网段，以减小广播所造成的影响。

通常三层交换机是采用模块化结构，以适应灵活配置的需要。在大中型网络中，第三层交换机已经成为基本配置设备。

要理解三层交换机的功能，首先需要先了解路由的概念。

第3层中的源端设备首先查看自己的路由表，路由表中包含了源IP地址、目的IP地址和子网掩码的所有信息。

然后，根据它从路由表中收集的信息，将数据包发送到目的地，并可以在不同的LAN、MAN和WAN网络之间进一步传递数据。

它遵循最短且安全的路径在终端设备之间传递数据，这就是路由的总体概念。

各种网络可以通过STM链路连接在一起，STM链路有很高的带宽，DS3链路也可以。连接的类型取决于网络的各种参数。

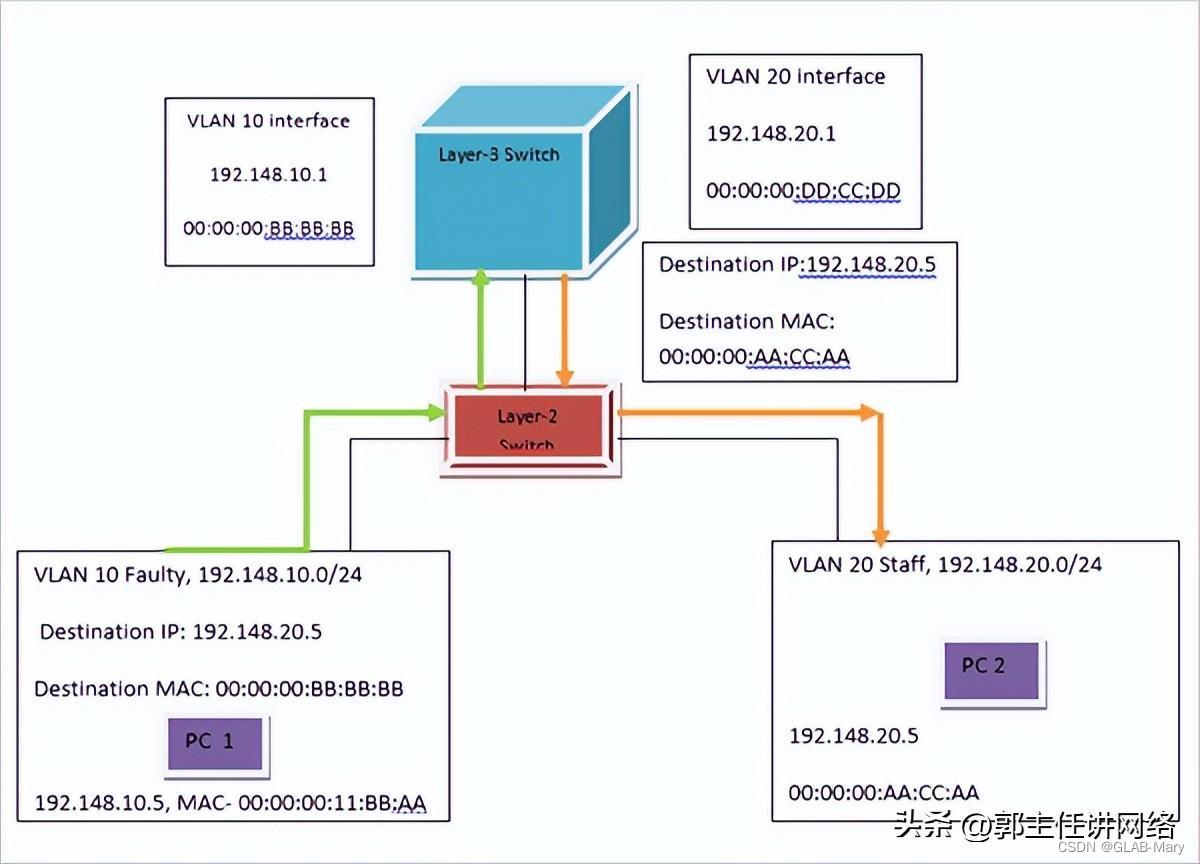
总结一下三层交换机的特点：

1. 执行静态路由，以在不同 VLAN 之间传输数据。而二层设备只能在同一 VLAN网络之间传输数据。

2. 以与路由器相同的方式执行动态路由，这种动态路由技术允许交换机执行最佳数据包路由。

3. 根据网络的实时场景提供一组多路径来传递数据包。交换机可以选择最可行的路径来路由数据包，目前流行的路由技术包括 RIP 和 OSPF。

4. 有能力识别关于流量流向的交换机的相关IP地址信息。

5. 能够根据子网划分或 VLAN 流量标记部署 QoS 分类，而不是像二层交换机那样手动配置交换机端口。

6. 需要更多的功率来运行，并在交换机之间提供更高带宽的链路，这些链路几乎超过 10Gbits。

7. 为数据交换提供高度安全的路径。

03 第四层交换机

OSI参考模型的第四层叫做传输层，该设备是采用第四层交换技术而开发出来的交换机产品，直接面对具体应用。

第四层交换机支持的协议是各种各样的，如HTTP，FTP、Telnet、SSL等。

在第四层交换中为每个供搜寻使用的服务器组设立虚IP地址（VIP），每组服务器支持某种应用。

在域名服务器（DNS）中存储的每个应用服务器地址是VIP，而不是真实的服务器地址。

当某用户申请应用时，一个带有目标服务器组的VIP连接请求（例如一个TCPSYN包）发给服务器交换机。

服务器交换机在组中选取最好的服务器，将终端地址中的VIP用实际服务器的IP取代，并将连接请求传给服务器。

这样，同一区间所有的包由服务器交换机进行映射，在用户和同一服务器间进行传输。

第四层交换技术相对原来的第二层、第三层交换技术具有明显的优点。

从操作方面来看，第四层交换是稳固的，因为它将包控制在从源端到宿端的区间中。

另一方面，路由器或第三层交换，只针对单一的包进行处理，不清楚上一个包从哪来、也不知道下一个包的情况。

它们只是检测包报头中的TCP端口数字，根据应用建立优先级队列，路由器根据链路和网络可用的节点决定包的路由，而第四层交换机则是在可用的服务器和性能基础上先确定区间。

总结来说，四层交换机与二层交换机、三层交换机的区别在于它们三者的工作方式以及应用方式的不同。

二层交换机的解决方案实际上是一个“处处交换”的廉价方案，虽然二层交换机的解决方案也能划分子网、限制广播、建立VLAN，但它的控制能力较小、灵活性不够，也无法控制各信息点的流量，缺乏方便实用的路由功能，只适合小型局域网。

三层交换机的交换机方案实际上是一个能够支持多层次动态集成的解决方案。

虽然。这种多层次动态集成功能在某些程度上也能由传统路由器和二层交换机搭载完成，但这种搭载方案与采用三层交换机相比，不仅需要更多的设备配置、占用更大的空间、设计更多的布线和花费更高的成本。

而且，数据传输性能也要差得多，因为在海量数据传输中，搭载方案中的路由器无法克服路由传输速率瓶颈。

四层交换机在网络中的应用非常灵活，它即可是网络中心的汇接点设备，又可以应用在局域网分布层的边缘接入处，甚至于作为工作组级支持交换到桌面。

目前，四层交换机主要技术除了实现网络负载均衡，还包括包过滤、服务质量、主备机连接等等。

随着信息应用水平的不断提高，它对网络的需求也越来越高，越来越复杂，四层交换机及类似的高层网络设备将在未来的网络环境中发挥更加重要的作用。

一文带你读懂二叉树

二叉树的基本概念

二叉树定义：结点的度最多为2

二叉树的五种形态：

• 空二叉树
• 只有一个根结点
• 根结点只有左子树
  
• 根结点只有右子树
• 根结点既有左子树又有右子树

特殊的二叉树：

• 斜树：分为左斜树和右斜树，其实这算是一种线性结构了

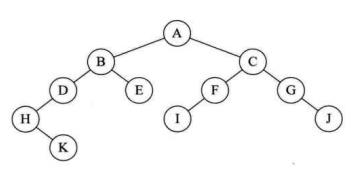
• 满二叉树：如图1所示。

• 完全二叉树：如图2所示。满二叉树一定是完全二叉树，但完全二叉树不一定是满的。而图3中的三颗树，都不是完全二叉树。
  

图1

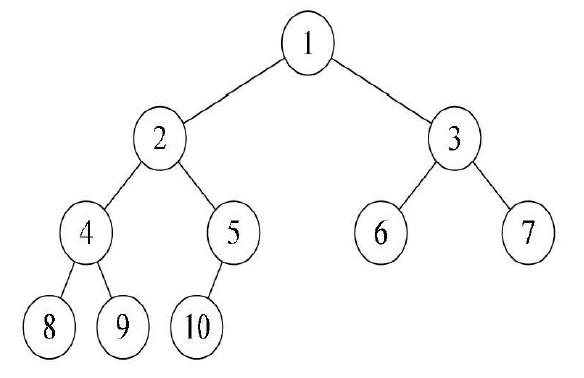
图2

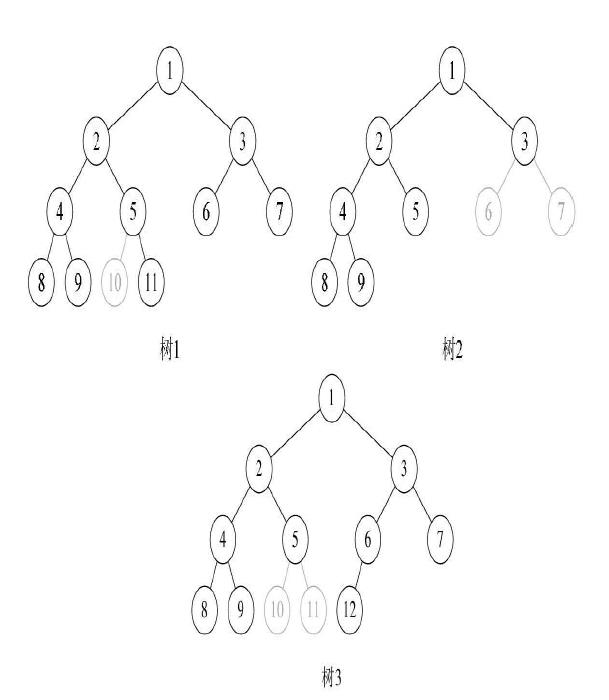
图3

二叉树的性质

1. 在二叉树的第i层上，最多有2^i-1个结点；

2. 深度为k的二叉树，最多有2^k-1个结点；

3. 对任何一棵二叉树T，如果其叶子结点数为n0，度为2的结点数为n2，则n0=n2+1；

4. 具有n个结点的完全二叉树的深度为|log₂n+1|（|x|表示不大于x的最大整数）；

5. 对一棵有n个结点的完全二叉树的结点按层序编号(从上到下从左到右，如图4所示)，对任一结点i（1≤i≤n）有：

• 结点i的左孩子为2i，右孩子为2i+1。
• 如果 i > n/ 2 ，则结点i无左孩子（结点i为叶子结点）。
  
• 如果i>(n-1)/2，则结点i无右孩子。

图4

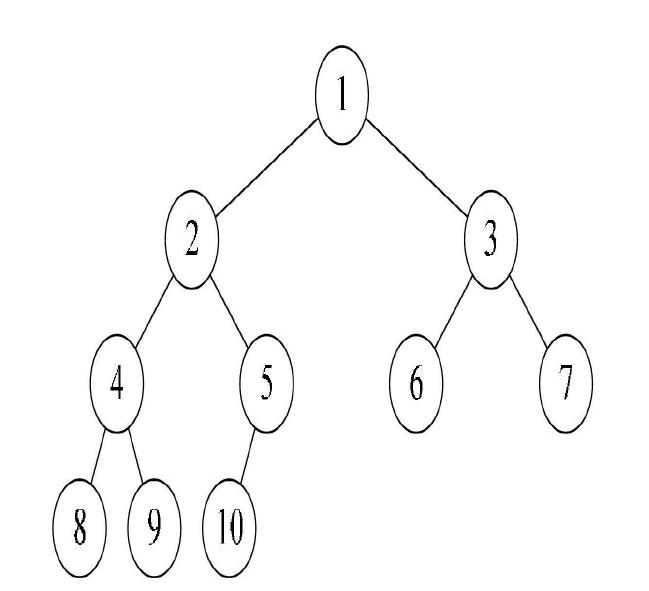
下面就来证明一下上述性质。1、2、4这个挺好理解的，无需证明。

关于第三点，为什么n0=n2+1呢？首先，n=n0+n1+n2这个是毫无疑问的。

然后将我们的注意力转移到分支线上，而不是结点上。

对于一颗有n个结点的二叉树来说，除了根结点头顶上没有分支线连接它，其余结点的头顶上有且仅有一条分支线与它对应，因此分支线总数=n0+n1+n2-1。

度为2的结点脚下有2条分支线，度为1的有1条，度为0的有0条，因此分支线总数=2*n2+n1。

根据上述标记为红色字体的两条公式，即可得出结论。

关于第五点，其实只用证明结点i的左孩子为2i即可，后面的结论都是根据这个结论而来的。下面的证明与图4有关。注意这是一颗完全二叉树。

首先我们证明这棵树的每一层的最左边结点i是否满足左孩子为2i(左孩子必然在该结点的下一层的最左边)。比如证明结点4的左孩子是否为8。假设结点4在k层(当然结点4在3层，k只是针对一般情况),那么结点4的值为2^k-1，结点4的左孩子的值为2^k，因此满足。

接下来证明不在每一层的最左边的结点i是否满足左孩子为2i。比如证明结点5的左孩子是否为10。设最左边的结点为i，结点5相对于本层最左边那个结点来说，偏移了n个单位（即结点5相对于结点4偏移了1个单位，n只是针对一般情况），结点5的值为i+n；其左孩子必然偏移2n个单位，结点5左孩子的值位2i+2n，因此满足。

二叉树的存储结构

对于一般的树来说，是不太适合用顺序存储结构来存储树的逻辑关系的，但是二叉树作为一种特殊的树，是可以这样做的。如下图所示。

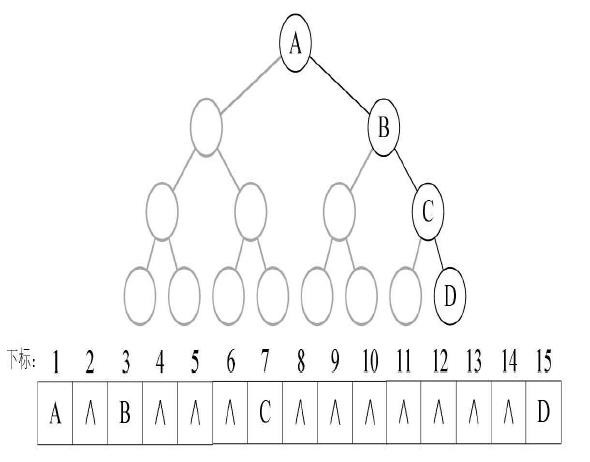
这张图表明用数组去存储一颗普通的二叉树，如果某个结点不存在，则用空值表示。对于普通二叉树来说，顺序存储显然是浪费空间的，因此顺序存储结构一般只适用于完全二叉树。

第二种就是用二叉链表了。因为作为一颗二叉树，很容易想到每个结点应该存储结点的值和左右孩子的指针，如果想快速找到某个结点的双亲，则还可以加一个双亲指针。二叉链表如下图所示。

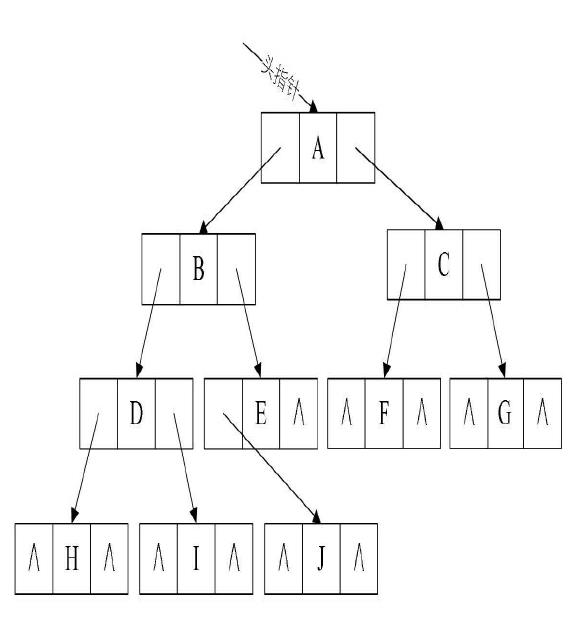
二叉树的遍历

二叉树的遍历： 按照一定的次序，将树中的所有结点遍历一次。

遍历方式：

• 前序遍历
  
• 中序遍历
• 后序遍历
• 层序遍历：从上到下、从左到右。

其中，前中后是相对于任一子树的根节点来说的。

下面用Java代码实现前中后三种遍历方式。

首先定义结点类。

public class Node{
    private Node left;
    private char data;
    private Node right;

    public Node(Node left, char data ,Node right) {
        this.left = left;
        this.right = right;
        this.data = data;
    }

    // 省略getter/setter方法
}

然后定义遍历类，该类有三个方法，分别对应前中后遍历，因为树的定义是采用递归思想的，因此树的遍历也采用了递归。另外该类还有一个构建树的方法，构建的树如下图所示。最后就是main方法了，相信大家都能看懂。

public class BinaryTreeTraverse {
    /**
     * 先序
     */
    public void firstTraverse(Node node){
        if(node == null){
            return;
        }
        System.out.print(node.getData());
        firstTraverse(node.getLeft());
        firstTraverse(node.getRight());
    }
    /**
     * 中序
     */
    public void middleTraverse(Node node){
        if(node == null){
            return;
        }
        middleTraverse(node.getLeft());
        System.out.print(node.getData());
        middleTraverse(node.getRight());
    }
    /**
     * 后序
     */
    public void laterTraverse(Node node){
        if(node == null){
            return;
        }
        laterTraverse(node.getLeft());
        laterTraverse(node.getRight());
        System.out.print(node.getData());
    }

    /**
     * 构建二叉树,并返回根结点
     */
    public Node buildTree(){
        Node node_k = new Node(null, 'K', null);
        Node node_h = new Node(null, 'h', node_k);
        Node node_d = new Node(node_h, 'd', null);
        Node node_e = new Node(null, 'e', null);
        Node node_b = new Node(node_d, 'b', node_e);
        Node node_i = new Node(null, 'i', null);
        Node node_j = new Node(null, 'j', null);
        Node node_f = new Node(node_i, 'f', null);
        Node node_g = new Node(null, 'g', node_j);
        Node node_c = new Node(node_f, 'c', node_g);
        Node node_a = new Node(node_b, 'a', node_c);
        return node_a;
    }

    public static void main(String[] args) {
        BinaryTreeTraverse traverse = new BinaryTreeTraverse();
        Node root = traverse.buildTree();
        //先序遍历
        traverse.firstTraverse(root);
        System.out.println();

        //中序遍历
        traverse.middleTraverse(root);
        System.out.println();
        //后序遍历
        traverse.laterTraverse(root);

    }

}

二叉树的建立

上面讲到了二叉树的遍历，但是如果我们的内存中都没有一颗二叉树，又哪来的遍历呢？因此下面我来讲讲二叉树的建立。

上面的例子中其实已经包含了二叉树的建立，但那是通过硬编码建立的，不符合一般情况。

我们可以通过二叉树的遍历结果反向构建二叉树。比如说先序遍历吧，可以根据其先序遍历结果来构建一颗二叉树，另外，我们还需要加一些虚结点，以保证能顺利地在内存中构建出一条二叉链条出来。

本次要构建的二叉树原型如下图所示。

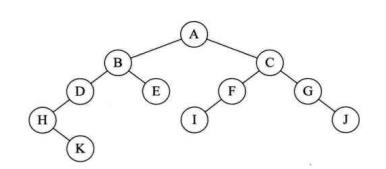
然后我们加一些虚节点，如下图所示。

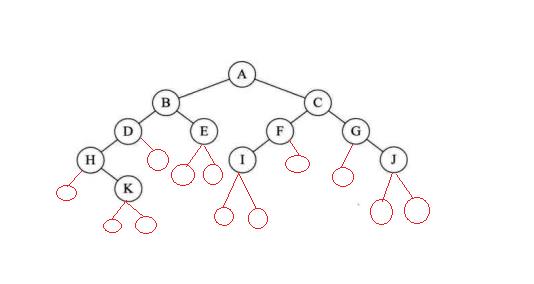
本来的先序遍历结果应该是：ABDHKECFIGJ，我们将虚结点记为#(别的符号也可以)，其先序遍历结果就变为了：ABDH#K###E##CFI###G#J##，这个很容易弄错，一定要仔细，否则输入（即将遍历结果视为输入，将构建出来的二叉树视为输出）都是错误的，那么构建出来的二叉树肯定也是错的。

二叉树的构建也由递归来实现，下面用Java代码实现通过先序遍历结果来构建一颗二叉树。

首先是结点Node类。

public class Node{
    private Node left;
    private char data;
    private Node right;

    public Node(Node left, char data ,Node right) {
        this.left = left;
        this.right = right;
        this.data = data;
    }
    // 省略getter/setter方法

    @Override
    public String toString() {
        return "Node{" +
                "left=" + (left==null?"null":left.getData()) +
                ", data=" + data +
                ", right=" + (right==null?"null":right.getData()) +
                '}';
    }
}

然后是具体的实现逻辑。

import java.util.ArrayList;
import java.util.List;

public class BinaryTreeBuilder {
    private List<Node> nodes;
    /**
     * 索引跟踪，每构建一个结点就加1，包括虚结点
     */
    private int index;

    /**
     * 构建某个结点,仅适用于先序构建
     * @param curIndex 该结点的索引，该索引不能只能存于方法客栈
     */
    public void buildNode(int curIndex){
        index++;
        //如果要构建的结点是个虚结点，那就不用构建左子树和右子树了，直接return；
        if(null == nodes.get(curIndex)){
            return;
        }
        // 递归构建左子树
        buildLeft(curIndex);
        // 递归构建右子树
        buildRight(curIndex);
    }

    /**
     * 构建左子树
     * @param curIndex 要构建左孩子的结点的索引
     */
    public void buildLeft(int curIndex){
        //设置左孩子
        nodes.get(curIndex).setLeft(nodes.get(index));
        //构建左孩子结点，因此传入的索引是左孩子的索引
        buildNode(index);
    }

    /**
     * 构建右子树
     * @param curIndex 要构建右孩子的结点的索引
     */
    public void buildRight(int curIndex){
        //设置右孩子
        nodes.get(curIndex).setRight(nodes.get(index));
        //构建右孩子结点，因此传入的索引是右孩子的索引
        buildNode(index);
    }

    public void initNodes(char[] arr){
        nodes = new ArrayList<>();
        for (char c : arr) {
            if(c=='#'){
                nodes.add(null);
            }else{
                nodes.add(new Node(null,c,null));
            }
        }
    }

    /**
     * 构建完成，打印构建结果
     */
    public void buildOK(){
        for (Node node : nodes) {
            if(null == node){
                continue;
            }
            System.out.println(node.getData()
                    +" -(左孩子->"+(node.getLeft()==null?"null":(node.getLeft().getData()+" "))+")"
                    +" -(右孩子->"+(node.getRight()==null?"null":(node.getRight().getData())+" ")+")");
        }
    }

    public void buildTree(char[] arr,String charArrType){
        initNodes(arr);
        if("先序构建".equals(charArrType)){
            buildNode(0);
        }else if("中序构建".equals(charArrType)){
            // 请参考buildNode先序构建方法，实现中序构建

        }else if("后序构建".equals(charArrType)){
            // 请参考buildNode先序构建方法，实现后序构建

        }else{
            return;
        }
        buildOK();
    }

    public static void main(String[] args) {
        BinaryTreeBuilder builder = new BinaryTreeBuilder();
        builder.buildTree("ABDH#K###E##CFI###G#J##".toCharArray(),"先序构建");
    }
}

最后运行程序，构建出来的结果如下图所示。

我仔细验证了一下，是没有问题的。至于根据中、后序遍历结果来构建二叉树的逻辑，由你们来动脑实现吧！