树二叉树森林
Posted sanweizuiji
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了树二叉树森林相关的知识,希望对你有一定的参考价值。
1 树的基本概念
树的度和m叉树
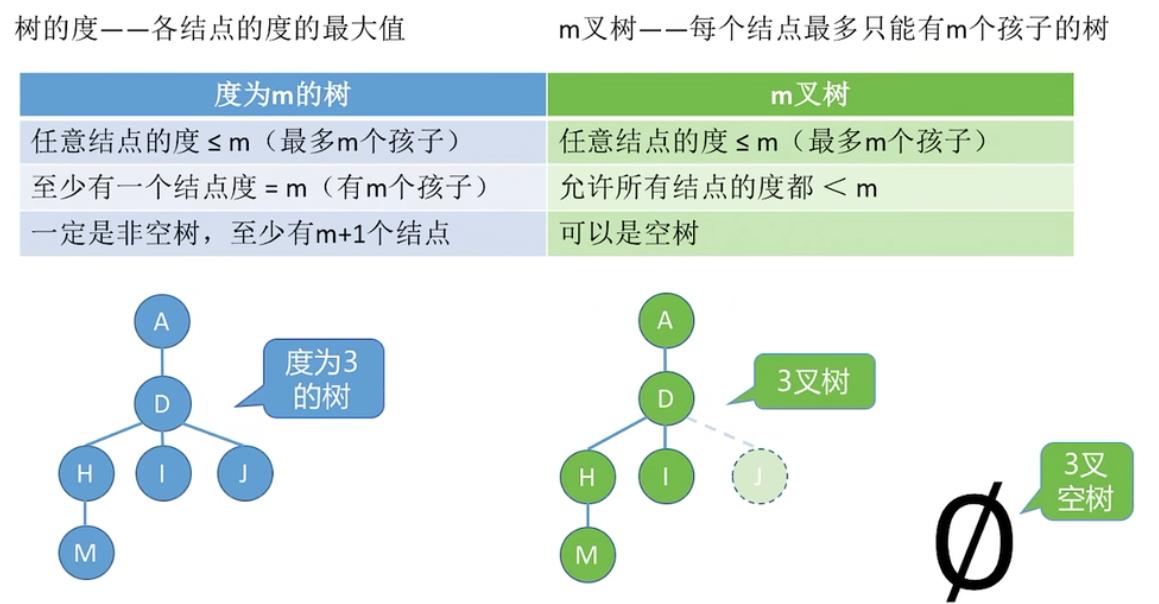
结点数 = 总度数 + 1 结点数=总度数+1 结点数=总度数+1
结点的度指的是结点有几个孩子(分支)
度为m的树
第i层至多有 m i − 1 m^i-1 mi−1个结点(i≥1)
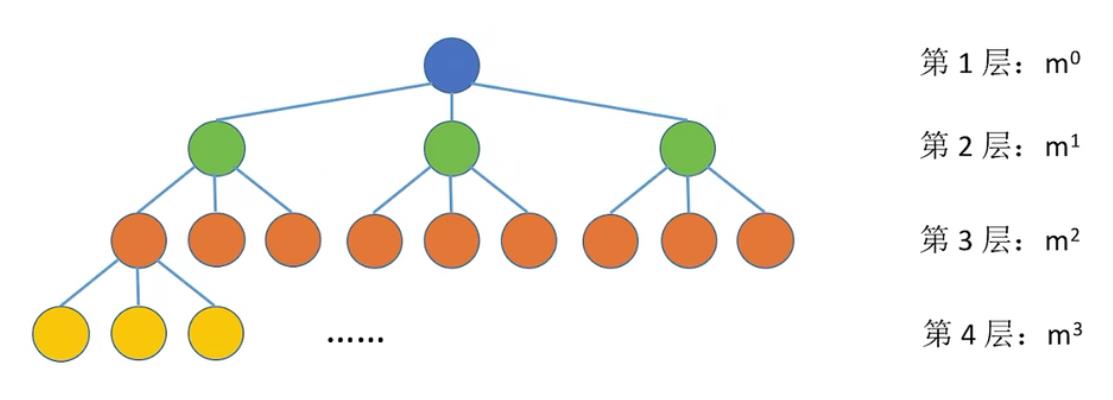
高度为h的m叉树

至多有个结点 1 − m h 1 − m \\frac1-m^h1-m 1−m1−mh
具有n个结点的m叉树的最小高度为
l o g m ( n ( m − 1 ) + 1 ) log_m(n(m-1)+1) logm(n(m−1)+1)
2 二叉树
基本概念与性质
叶子结点比二分支结点多一个
设非空二叉树中度为0、1和2的结点个数分别为n0、n1和n2,则n0= n2 + 1

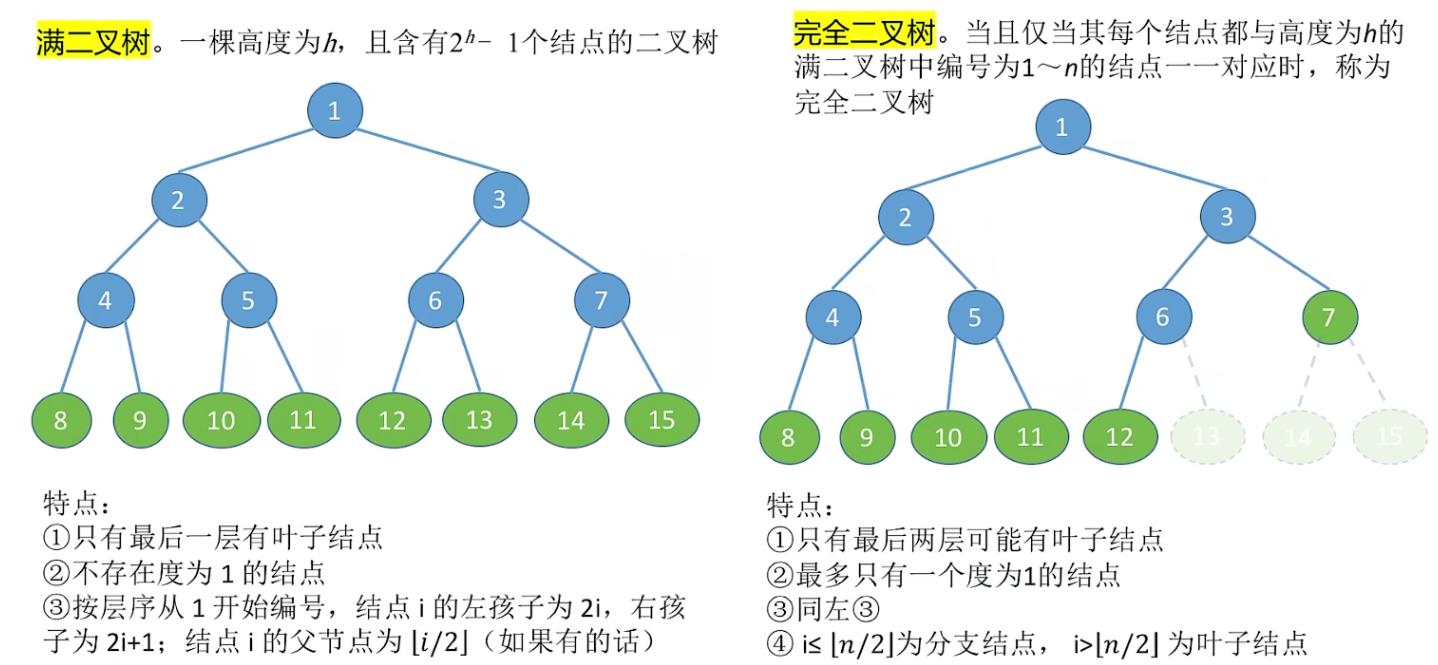
满二叉树
完全二叉树
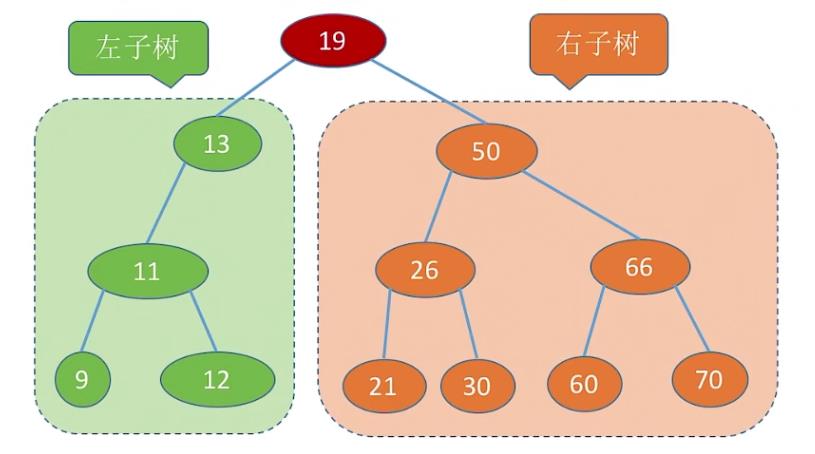
二叉排序树
一棵二叉树或者是空二叉树,或者是具有如下性质的二叉树
左子树上所有结点的关键字均小于根结点的关键字
右子树上所有结点的关键字均大于根结点的关键字
左子树和右子树又各是一棵二叉排序树
平衡二叉树
树上任一结点的左子树和右子树的深度之差不超过1
二叉树的实现
顺序存储结构
链式存储结构
3 遍历二叉树及其应用(任何一棵二叉树的叶子结点在前序、中序和后序遍历序列中的相对次序都不发生改变)
先序遍历二叉树
#include <stdio.h>
#include <malloc.h>
// 自定义树的节点
typedef int treeElementDataType;
struct myBinaryTreeNode
treeElementDataType data;
struct myBinaryTreeNode *leftChild;
struct myBinaryTreeNode *rightChild;
;
typedef struct myBinaryTreeNode BinaryTreeNode;
void printTreeNode(BinaryTreeNode *node)
printf("%d", node->data);
// 先序遍历(先根遍历)
void preOrder(BinaryTreeNode *node)
if (node != NULL)
printTreeNode(node);
preOrder(node->leftChild);
preOrder(node->rightChild);
中序遍历二叉树
// 中序遍历
void inOrder(BinaryTreeNode *node)
if (node != NULL)
inOrder(node->leftChild);
printTreeNode(node);
inOrder(node->rightChild);
后序遍历二叉树
// 后序遍历
void postOrder(BinaryTreeNode *node)
if (node != NULL)
postOrder(node->leftChild);
postOrder(node->rightChild);
printTreeNode(node);
// 求树的深度
int treeDepth(BinaryTreeNode *node)
if (node == NULL)
return 0;
else
int leftDepth = treeDepth(node->leftChild);
int rightDepth = treeDepth(node->rightChild);
return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
层次遍历二叉树
// ----------------------------------------------- 此块为队列的基本操作,需将队列元素的数据类型改为树的结点的指针
// 这里灵活定义队列元素的数据类型,因为后续可能将树的结点的指针作为数据类型
// typedef int queueElementDataType;
typedef BinaryTreeNode *queueElementDataType;
// 自定义队列元素结构体
struct myQueueElement
queueElementDataType data;
struct myQueueElement *next;
;
typedef struct myQueueElement QueueElement;
// 自定义队列结构体
struct myQueue
QueueElement *front, *rear;
;
typedef struct myQueue Queue;
Queue *initQueue()
QueueElement *queueElement = (QueueElement *) malloc(sizeof(QueueElement));
Queue *queue = (Queue *) malloc(sizeof(Queue));
// 初始化时 front rear 都指向头结点
queue->front = queue->rear = queueElement;
queue->front->next = NULL;
return queue;
// 返回入队后的队列
Queue *enQueue(Queue *queue, queueElementDataType x)
QueueElement *s = (QueueElement *) malloc(sizeof(QueueElement));
s->data = x;
s->next = NULL;
// 将新节点入队
queue->rear->next = s;
// 将尾指针后移
queue->rear = s;
return queue;
// 返回出队后的队列
Queue *deQueue(Queue *queue)
if (queue->front == queue->rear)
printf("队列为空\\n");
else
// temp 为队头结点
QueueElement *temp = queue->front->next;
queue->front->next = temp->next;
// 如果此时出队的结点刚好是最后一个结点
if (temp == queue->rear)
// 那么在修改头结点的指向后,还要将尾指针指向头结点
queue->rear = queue->front;
free(temp);
return queue;
queueElementDataType getFirstElementData(Queue *queue)
return queue->front->next->data;
void printQueue(Queue *queue)
printf("----- 当前队列 -----\\n");
printf("从上至下代表从队头到队尾\\n");
// temp 为队头元素
QueueElement *temp = queue->front->next;
while (temp != NULL)
// 这里需要根据 queueElementDataType 的类型来决定如何打印
printf("%d\\n", temp->data);
temp = temp->next;
// ----------------------------------------------- 此块为队列的基本操作,需将队列元素的数据类型改为树的结点的指针
// 使用队列按层次遍历(BFS)
void levelOrder(BinaryTreeNode *root)
// 新建队列用来存储二叉树结点的数据
Queue *queue;
queue = initQueue();
BinaryTreeNode *temp;
// 树根入队
queue = enQueue(queue, root);
while (queue->front != queue->rear)
// 先保存即将出队的队头元素
temp = getFirstElementData(queue);
// 再进行出队操作
queue = deQueue(queue);
printTreeNode(temp);
// 如果左孩子不为空,则将左孩子的数据入队
if (temp->leftChild != NULL)
queue = enQueue(queue, temp->leftChild);
// 如果右孩子不为空,则将右孩子的数据入队
if (temp->rightChild != NULL)
queue = enQueue(queue, temp->rightChild);
4 线索树
线索二叉树知道了“前驱”和“后继”信息,就可以把二叉树看作一个链表结构,从而可以像遍历链表那样来遍历二叉树,进而提高效率。
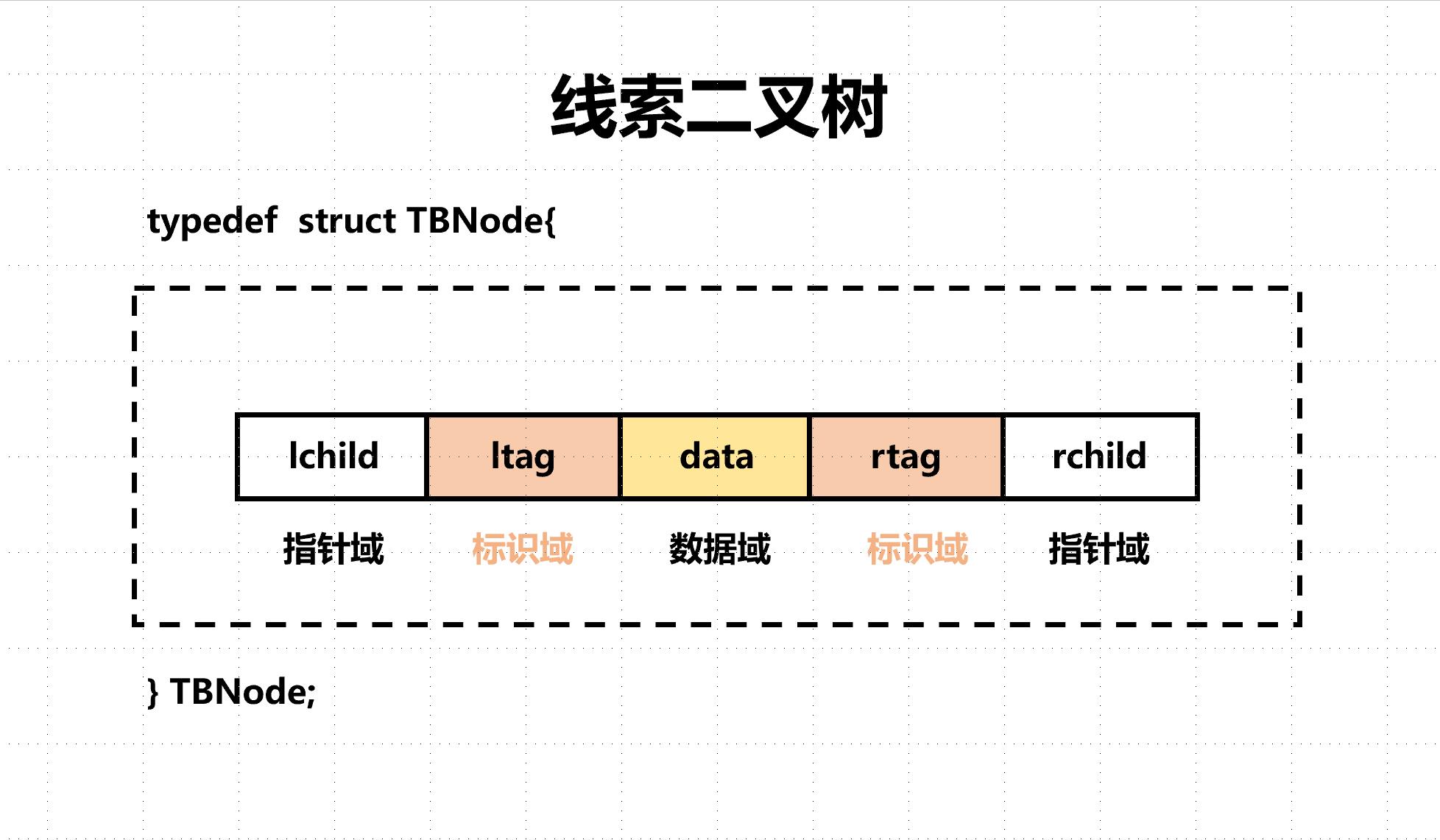
如果ltag=0,表示指向节点的左孩子。如果ltag=1,则表示lchild为线索,指向节点的直接前驱
如果rtag=0,表示指向节点的右孩子。如果rtag=1,则表示rchild为线索,指向节点的直接后继
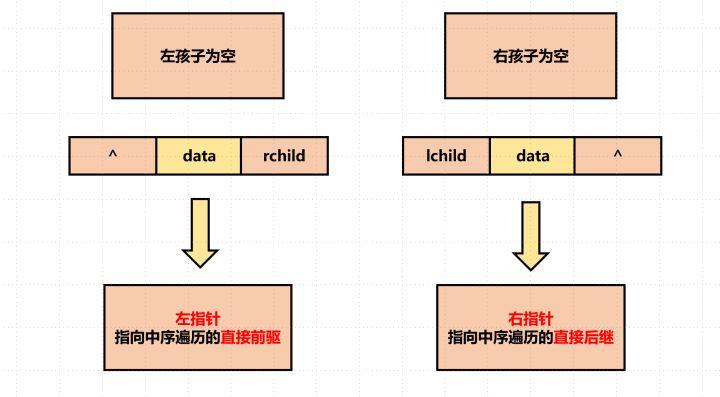
例 在线索化树中,每个结点必须设置一个标志来说明它的左、右链指向的是树结构信息还是线索化信息,若0标识树结构信息,1标识线索,对应叶结点的左右链域,应标识为(11)
叶节点没有必要标注左右子节点了,所以直接标记为线索,然后根据有无前后继再决定是否将线索指为空
例 线索二叉树的左线索指向其(遍历序列中的前驱),右线索指向(其遍历序列中的后继)
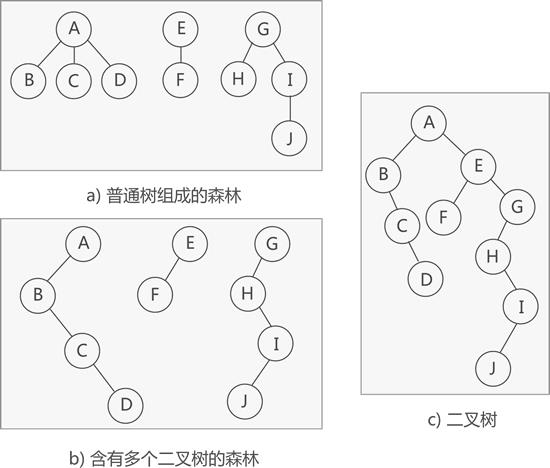
5 二叉树与森林
6 二叉排序树和平衡二叉树
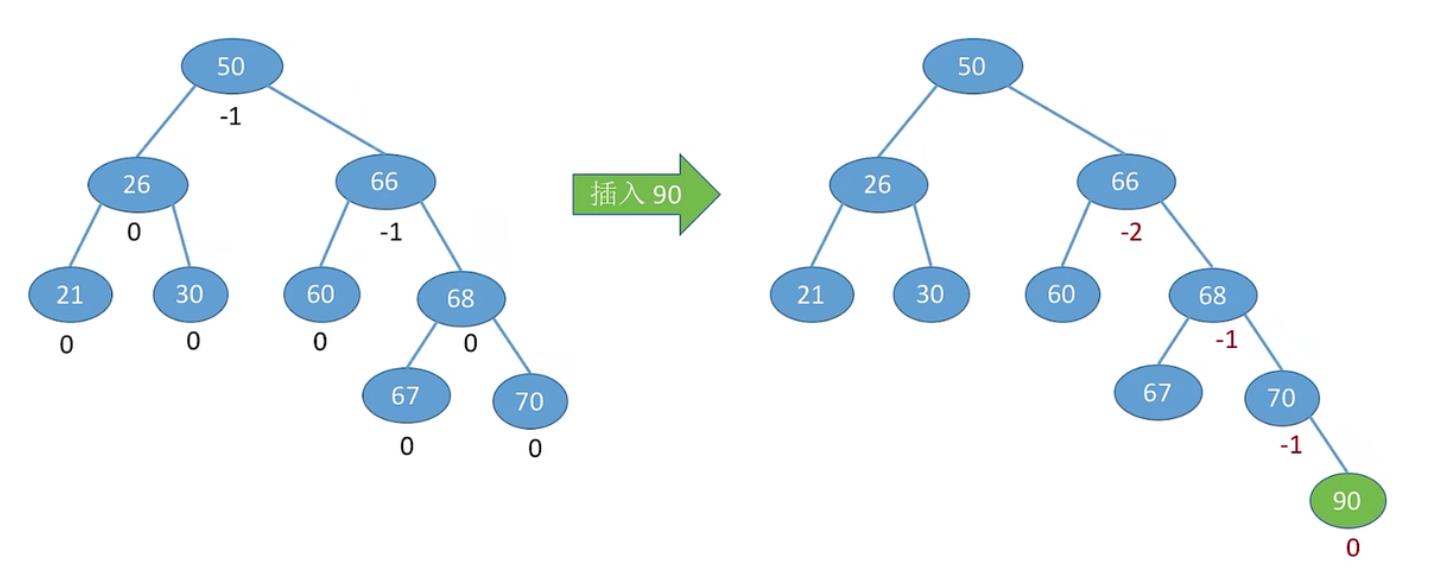
6.1 最小不平衡树的右孩子的右子树上插入元素
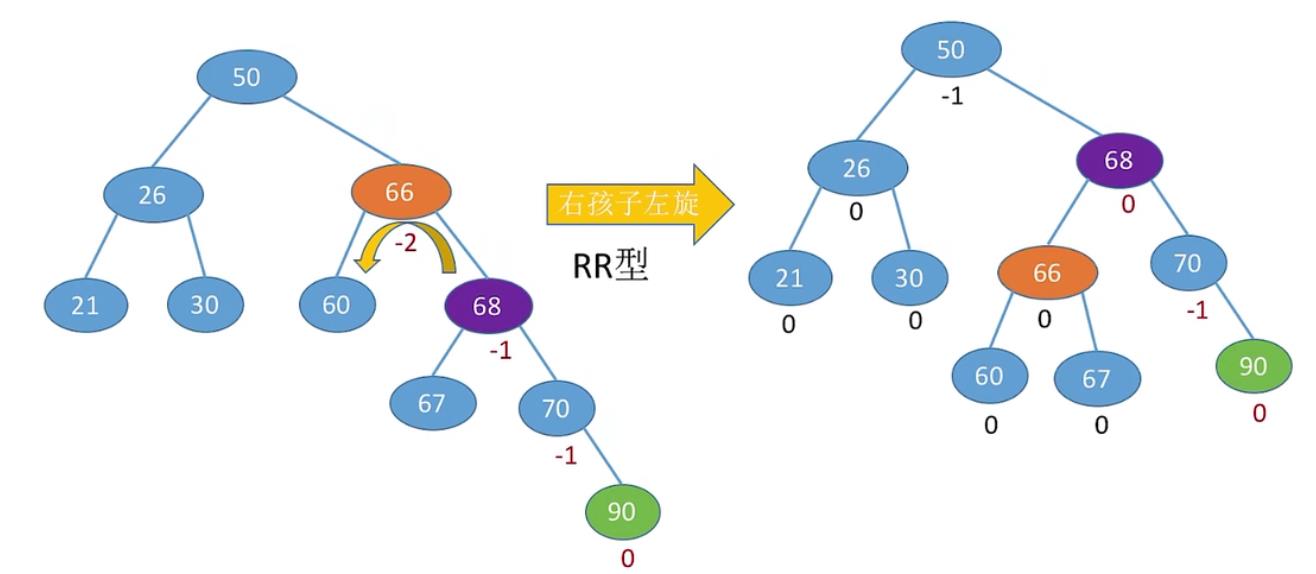
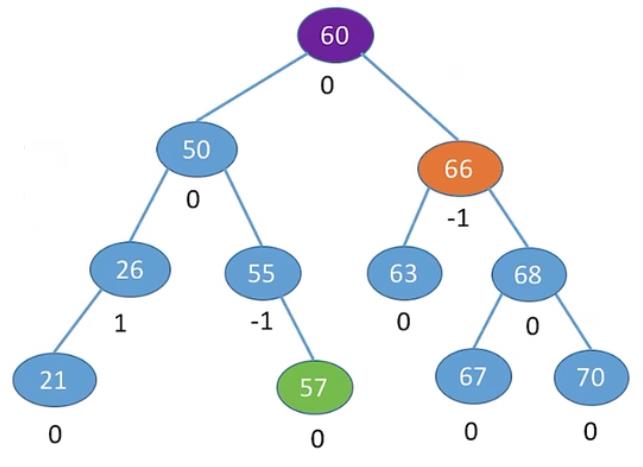
6.2 最小不平衡树的右孩子的左子树上插入元素
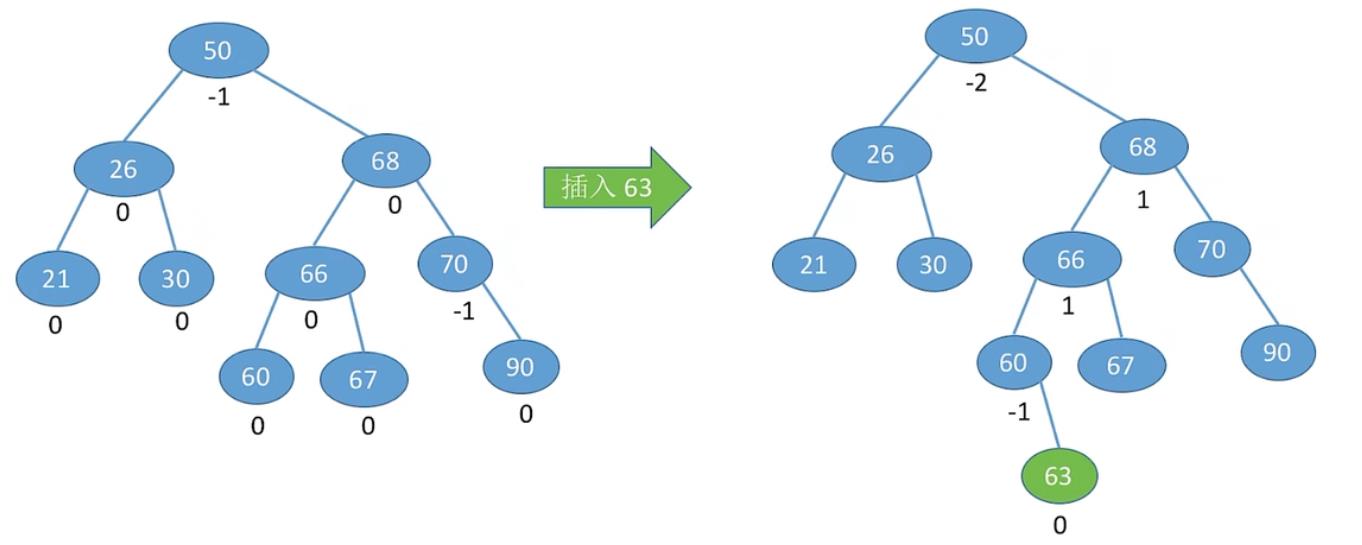
右旋+左旋 结点66
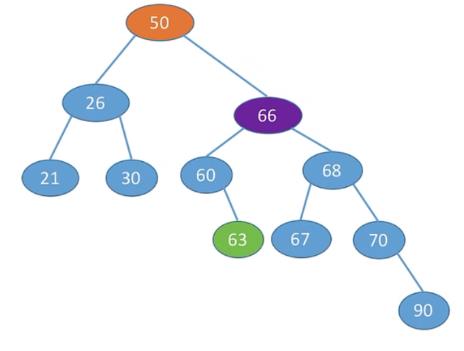
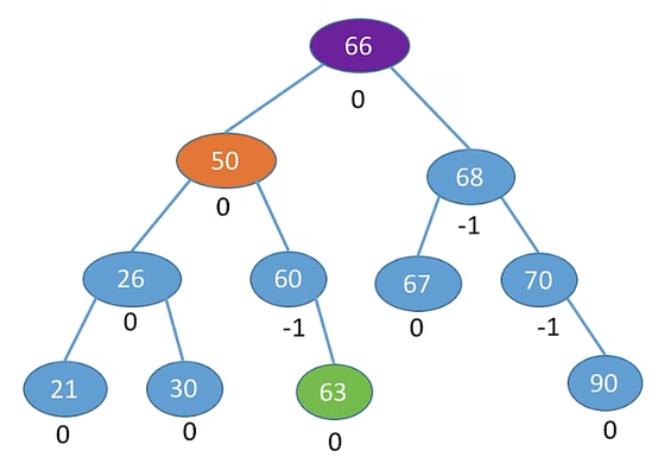
6.3 最小不平衡树的左孩子的左子树上插入元素
6.4 最小不平衡树的左孩子的右子树上插入元素
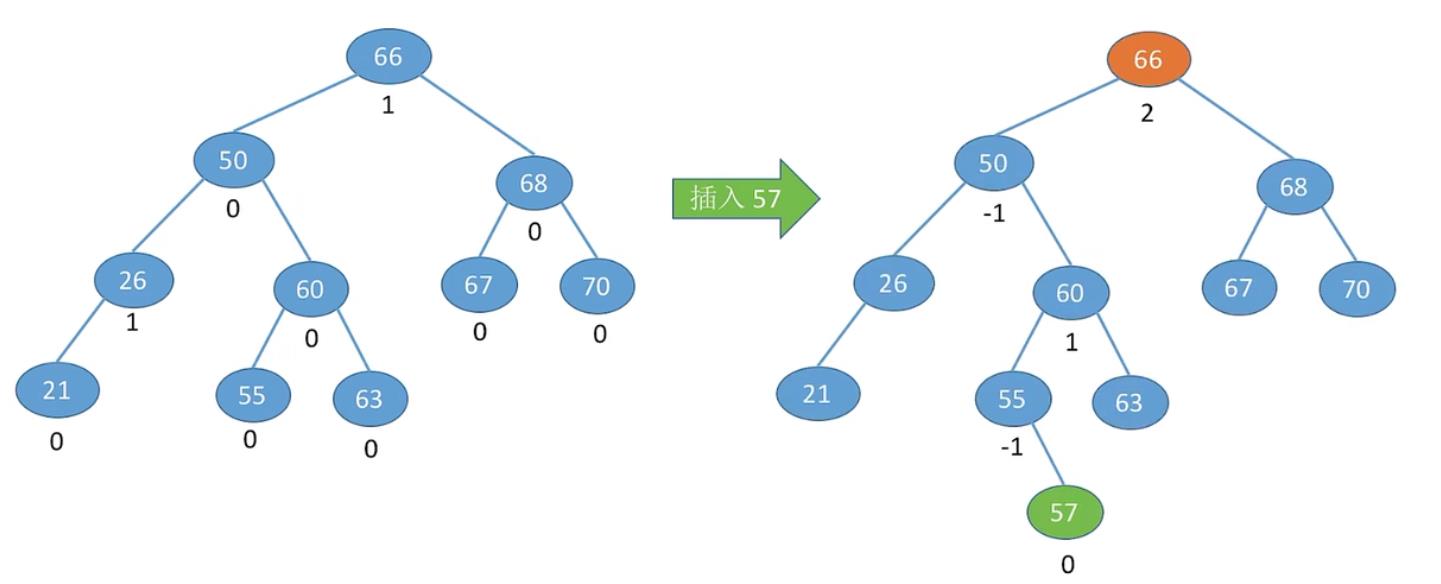
左旋+右旋 结点60
7 哈夫曼树
例 一棵有n个叶子结点的哈夫曼树共有(2n-1)个结点
以上是关于树二叉树森林的主要内容,如果未能解决你的问题,请参考以下文章