小呆的力学笔记非线性有限元的初步认识

Posted 2023-04-05 努力的骆驼

文章目录

• • 0. 有限元方法的诞生
  • 1. 线性有限元的初步认识
  • • 1.1 弹性力学概述
    • • 1.1.1 弹性力学基本假设
      • 1.1.2 平衡方程
      • 1.1.2.A 平衡方程的探讨
      • 1.1.3 几何方程
      • 1.1.3.A 几何方程的探讨
      • 1.1.4 本构方程
      • 1.1.4.A 本构方程的探讨
      • 1.1.5 边界条件
      • 1.1.5.A 边界条件的探讨
      • 1.1.6 线弹性力学的总结
      • 1.1.6 非线性有限元与线性有限元的区别点

0. 有限元方法的诞生

有限元方法是仿真模拟的重要方法，特别是在结构仿真中占据主导地位。从本质上来说，有限元方法和有限差分法等方法一样，都是一种求解物理方程的数值计算方法。计算机技术的迅猛发展使得数值仿真应用越来越广泛，有限元方法作为重要仿真工具内容也越来越丰富。
有限元方法从诞生之初就是为了 方便求解工程实际中的力学问题。1943年，Courant最先尝试使用三角形区域的多项式函数来求解结构静力学和振动问题。1956年，波音公司工程师Turner等人系统性的研究了离散结构的单元刚度问题，同时率先应用这种离散方法正确处理了飞机结构工程中的实际问题。这种离散方法的成功应用激起了工程师的热情，越来越多的工程师使用这种方法处理结构分析问题、流体力学问题、热传导问题等各种工程问题。1960年，波音工程师Clough第一次将这种方法命名为“有限元方法”。
在工程应用的同时，数学家通过研究发现通过能量泛函的极值问题或加权残差法能够导出有限元方法，坚实了有限元方法的数学基础。有限元方法最早应用和发展的主要集中在线性问题，特别对于结构分析来说，大部分的工程实际结构都满足小变形假设，材料也工作在弹性范围，那么线性有限元就能够解决大部分的问题。
随着有限元应用越来越广泛，更多的应用场景不能通过线性有限元来分析模拟了，例如：汽车的碰撞问题，航空发动机叶片脱落问题，金属薄板的加工成型问题，橡胶等超弹性材料的受力变形问题等等。这些问题都需要用非线性有限元的方法来仿真模拟。

1. 线性有限元的初步认识

学习非线性有限元之前先复习线性有限元理论。线性有限元分析的力学基础是弹性力学，来复习一下弹性力学知识。

1.1 弹性力学概述

1.1.1 弹性力学基本假设

在弹性力学研究的范围内，先得明确五个基本假设：
（1）连续性假设：该假设认为在弹性力学研究的范畴内，物体呈现其宏观尺度上的连续性特性，事实上，所有物质本质上均为不连续，但在远大于粒子尺度上（强力和弱力作用范围$10^{-15}$、$10^{-18}$，远小于弹性力学研究范围），物质往往表现出连续性的特性。
（2）均匀性假设：该假设认为物体内材料处处均匀。事实上，这往往是不成立的，学过金属材料的都知道，金属作为多晶体物质，内部存在大大小小各异的晶粒，晶粒间还有晶界，还有成形过程中的析出相等等，所以材料肯定不是处处均匀。不过在弹性力学研究的范畴内，材料往往可以处理成处处均匀，也不至于很大误差。
（3）各向同性假设：该假设认为物体内各点的材料各方向的力学特性相同。这对很多金属材料适用。弹性力学仅仅是为了简化研究对象，本质上各项异性不影响弹性力学的研究。
（4）线弹性假设：该假设认为在弹性力学研究中的物体材料变形和受到的外力呈线性关系。这是限定弹性力学适用范围的条件一。
（5）小变形假设：该假设认为在弹性力学研究中物体的变形比较小，转动更小，变形前后物体的几何形状、尺寸和位置不至于发生较大的变化。这是限定弹性力学适用范围的条件二。

1.1.2 平衡方程

此外，还需要引入微元体作为研究对象，三维的微元体见下图，微元体的各边长为dx、dy、dz，其中微元体表面的法向与坐标正方向一致的都用黑色箭头和黑色字体，表面的法向与坐标负方向一致的都用蓝色箭头和字体，微元体面上的应力按照如下的规则定义。

\\quad\\quad\\quad\\quad\\quad\\quad\\quad\\quad\\quad 图1.1.1 微元体应力示意图
从牛顿第二定理（动量定理）可以列出微元体的平衡方程，如下所示：
$$\begin{gathered} {\sigma }_{xx}(x+dx,y,z)dydz-{\sigma }_{xx}(x,y,z)dydz+{\tau }_{xy}(x,y+dy,z)dxdz-{\tau }_{xy}(x,y,z)dxdz \\ +{\tau }_{xz}(x,y,z+dz)dxdy-{\tau }_{xz}(x,y,z)dxdy+b_{x}dxdydz=\rho \ddot{u}dxdydz\text{\hspace{1em}(1-1)} \end{gathered}$$
$$\begin{gathered} {\tau }_{yx}(x+dx,y,z)dydz-{\tau }_{yx}(x,y,z)dydz+{\sigma }_{yy}(x,y+dy,z)dxdz-{\sigma }_{yy}(x,y,z)dxdz \\ +{\tau }_{yz}(x,y,z+dz)dydz-{\tau }_{yz}(x,y,z)dydz+b_{y}dxdydz=\rho \ddot{v}dxdydz\text{\hspace{1em}(1-2)} \end{gathered}$$
$$\begin{gathered} {\tau }_{zx}(x+dx,y,z)dydz-{\tau }_{zx}(x,y,z)dydz+{\tau }_{zy}(x,y+dy,z)dxdz-{\tau }_{zy}(x,y,z)dxdz \\ +{\sigma }_{zz}(x,y,z+dz)dxdy-{\sigma }_{zz}(x,y,z)dxdy+b_{z}dxdydz=\rho \ddot{w}dxdydz\text{\hspace{1em}(1-3)} \end{gathered}$$
其中b为单位体积的体积力。选择上面第一个公式，将应力按一阶泰勒展开，则上式如下：

( σ x x ( x , y , z ) + ∂ σ x x ( x , y , z ) ∂ x d x ) d y d z − σ x x ( x , y , z ) d y d z + (

《机器人控制系统和MATLAB simulink仿真》笔记1：认识S函数

前言

最近在看控制的东西，想动手实践一下，看到有书名曰《机器人控制系统和MATLAB simulink仿真》，于是学习一下做做产出

1.认识对象：机器人动力学系统的特性

考虑一个关节机器人，其动态性能可由二阶非线性微分方程描述：

$$\mathbf{M}(\mathbf{q})\ddot{\mathbf{q}}+\mathbf{C}(\mathbf{q},\dot{\mathbf{q}})\dot{\mathbf{q}}+\mathbf{G}(\mathbf{q})+\mathbf{F}(\dot{\mathbf{q}})+{\mathbf{\tau }}_{\mathrm{d}}=\mathbf{\tau }$$

其中，$\mathbf{q}\in {\mathbb{R}}^n$为关节角位移量，$\mathbf{M}(\mathbf{q})\in {\mathbb{R}}^{n\times n}$为机器人的惯性矩阵，$\mathbf{C}(\mathbf{q},\dot{\mathbf{q}})\dot{\mathbf{q}}\in {\mathbb{R}}^n$表示离心力和哥氏力，$\mathbf{G}(\mathbf{q})\in {\mathbb{R}}^n$为重力项，$\mathbf{F}(\dot{\mathbf{q}})\in {\mathbb{R}}^n$表示摩擦力矩，$\mathbf{\tau }\in {\mathbb{R}}^n$为控制力矩，${\mathbf{\tau }}_{\mathrm{d}}\in {\mathbb{R}}^n$为外加扰动。

机器人系统的动力学特性为：

（书中没有对这些特性严格地证明，后面还得再琢磨一下）

2.S函数

2.1 S函数简介

S函数是Simulink的重要部分，它为Simulink环境下的仿真提供了强有力的拓展能力。它用文本方式输入公式和方程，适合复杂动态系统的数学描述，并且在仿真过程中可以对仿真参数进行更精确的描述。机器人控制系统的Simulink仿真中，可以使用S函数来实现控制律、自适应律和被控对象的描述。

2.2 S函数使用步骤

一般而言，S函数的使用步骤如下：

(1)创建S函数源文件。创建S函数源文件有多种方法，Simulink提供了很多S函数模板和例子，用户可以根据自己的需要修改相应的模板或例子即可。

(2)在动态系统的Simulink模型框图中添加S-function模块，并进行正确的设置。

(3)在Simulink模型框图中按照定义好的功能连接输入输出端口。为了方便S函数的使用和编写，Simulink的Functions&.Tables模块库还提供了S-functiondemos模块组，该模块组为用户提供了编写S函数的各种例子，以及S函数模板模块。

2.3 S函数的基本功能及重要参数

S函数的基本功能及重要参数设定如下：

(1)S函数功能模块：各种功能模块完成不同的任务，这些功能模块（函数）称为仿真例程或回调函数(call-back functions),包括初始化(initialization)、导数(mdlDerivative)、输出(mdlOutput)等。

(2)NumContStates表示S函数描述的模块中连续状态的个数。

(3)NumDiscStates表示离散状态的个数。

(4)NumOutputs和NumInputs分别表示模块输出和输入的个数。

(5)直接馈通(dirFeedthrough)为输入信号是否在输出端出现的标识，取值为0或1.例如，形如$y=k\times u$的系统需要输入（即直接反馈），其中，$u$是输入，$k$是增益，$y$是输出，形如等式$y=x,x=\dot{u}$的系统不需要输入（即不存在直接反馈），其中，$x$是状态，$u$是输入，$y$为输出。

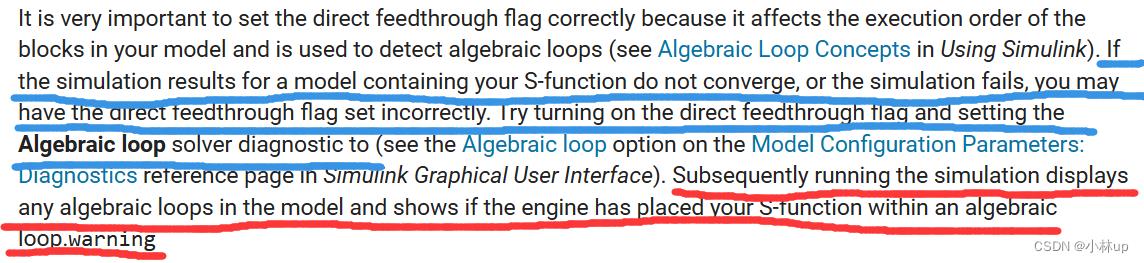
(6)NumSampleTimes为模块采样周期的个数，S函数支持多采样周期的系统。

除了sys外，还应设置系统的初始状态变量$x_o$、说明变量$str$和采样周期变量$t_s$。t变量为双列矩阵，其中每一行对应一个采样周期。对连续系统和单个采样周期的系统来说，该变量为$[t_1,t_2]$, $t_1$为采样周期，$t_1=-1$表示继承输入信号的采样周期，$t_2$为偏移量，一般取为$0$。对继承输入信号的采样周期的连续系统来说，$t$取为$[一1,0]$。

有关采样周期变量的含义更详细的摘录官方文档的内容：
采样周期的取值

如何选择采样时间：

关于以上dirFeedthroug和NumSampleTimes的内容可以参考官方文档理解得更详细：

S-Function Concepts

2.4 S函数的使用实例

以下面的公式为例

$$J\ddot{\theta }=u+d(t)$$

$u$为控制输入,$d(t)$为加在控制输人端的扰动,模型输出为角度$\theta$和角速度$\dot{\theta }$，$J$是转动惯量，模型描述为：

$$\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=\frac{1}{J}(u+d(t))\end{array}$$

其中$x_1=\theta ,x_2=\dot{\theta }$是状态变量。

2.4.1 模型初始化Initialization函数

上述动力学方程是1输入2输出系统，角度$\theta$和角速度$\dot{\theta }$的初始值为0，模型初始化参数为[0,0]，模型初始化S函数为：

function [sys,x0,str,ts]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates  = 2;%连续状态个数为2：x_1和x_2，因为采用连续采样周期仿真
sizes.NumDiscStates  = 0;%离散状态个数为0
sizes.NumOutputs     = 2;%输出量为2个：角度和角速度
sizes.NumInputs      = 1;%输入量为1个，u
sizes.DirFeedthrough = 0;%方程中输入没有直馈于输出
sizes.NumSampleTimes = 1;%采样周期数是1
sys simsizes(sizes);
x0=[0,0]:%初始化输出值角度和角速度都是0
str=[]:%无其他说明
ts=[0 0]:%连续采样，第一个值为0，没有偏移，第二个值也设为0

2.4.2 微分方程描述的mdlDerivative函数

该函数可用于描述微分方程并实现数值求解。在控制系统中，可采用该函数来描述，被控对象和自适应律等，并通过Simulink环境下选择数值分析方法(如ODE方法)实现模型的数值求解。取$J=2$,$d(t)=\sin t$,则采用S函数可实现该模型角度$\theta$和角速度$\dot{\theta }$的求解，描述如下：

function sys=mdlDerivatives(t,x,u)%sys
J=2;
dt=sin(t);
ut=u(1);
sys(1)=x(2):%左边的sys是状态变量的导数
sys(2)=1/J (ut+dt);

2.4.3 用于输出的mdlOutput函数

S函数的mdlOutput函数通常用于描述控制器或模型的输出。采用S函数的mdlOutput模块来描述模型角度$\theta$和角速度$\dot{\theta }$的输出：

function sys mdlOutputs(t,x,u)
sys(1)=x(1):
sys(2)=x(2):