线性代数的一些知识点
Posted Icy Hunter
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了线性代数的一些知识点相关的知识,希望对你有一定的参考价值。
文章目录
行列式
逆序数
容易理解,就是小的在大的后面就是有一个逆序

三阶行列式计算

符号怎么确定呢?
就需要用到逆序数了。

三阶行列式可以如上定义计算,符号与排列的逆序数奇偶有关。
n阶行列式

不过一般都是降到三阶再计算行列式。
行列式的性质
-
行列式与它的转置行列式相等
-
对换行列式的两行(列),行列式变号 =>如果两行相同则行列式为0
-
行列式的某一行(列)中的所有元素都乘同一数k,等于用数k乘此行列式=>行列式中某一行(列)的所有公因子可以提到行列式记号外面。

-
行列式中如果有两行(列)元素成比例,则此行列式为0
-
若行列式的某一行(列)的元素都是两数之和,可以对应元素拆出两个行列式。

-
把行列式的某一行(列)的各个元素乘同一数然后加到另一行(列)对应的元素上去,行列式不变。

余子式和代数余子式


代数余子式就是多了个符号

行列式展开
有了这两个概念就可以对行列式进行降阶了:


看个例子感悟一下:

矩阵及其运算
非齐次线性方程和齐次线性方程

一些矩阵的命名

一些矩阵的概念

矩阵运算
矩阵加法

数与矩阵相乘

矩阵相乘

矩阵相乘的法则

矩阵运算不满足交换律
矩阵的转置运算:

方阵的行列式计算:

伴随矩阵

逆矩阵:

其实也说明,矩阵有逆,那么这个矩阵应该是一个方阵。
逆矩阵的运算规则

克拉默法则:


其中|A1|就是系数矩阵第一列元素换成右端常数项后得到的n阶矩阵,A2…以此类推。
矩阵的初等变换与线性方程组
矩阵初等
矩阵初等变换有三种形式

看个例子感悟一下:
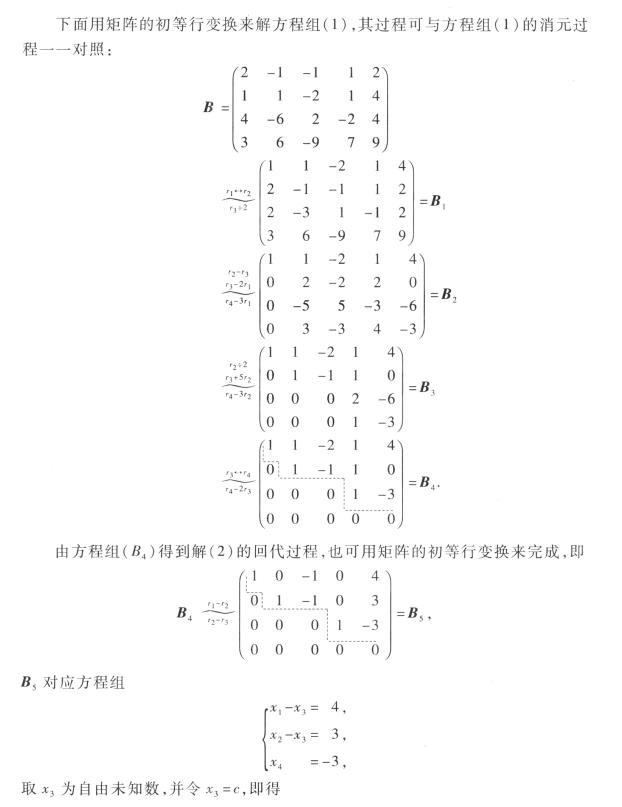
B矩阵为系数矩阵+偏置矩阵
最终化为的形式为行阶梯形矩阵
当行阶梯形矩阵满足(1)非零行的首非零元为1;(2)首非零元所在的列的其他元均为0,则称此矩阵为行最简矩阵。

矩阵的秩
简单来说就是将矩阵化成行阶梯形矩阵,有多少行非零,则秩就是多少。

线性方程组解的情况
知道了如何求矩阵的秩
就可以来求解线性方程组解的情况了:


来个例子感悟一下:


总结
线性代数还是很重要的!以后还会再来补
参考
工程线性代数第六版-同济大学数学系 编
以上是关于线性代数的一些知识点的主要内容,如果未能解决你的问题,请参考以下文章