C++学习（一三九）floatdouble的有效数字

Posted 2022-09-07 hankern

具体参考《IEEE标准754》

结论为：

float有效数字位为6 – 7位，第7位不一定有效，字节数为4，指数长度为8位，小数长度为23位。取值范围为 3.4E-38～3.4E+38。对于9999999，其实为10000000。

double有效数字位为15 – 16位，第16位不一定有效，字节数为8，指数长度为11位，小数长度为52位。取值范围为1.7E-308～1.7E+308。

浮点数的内部存储为：

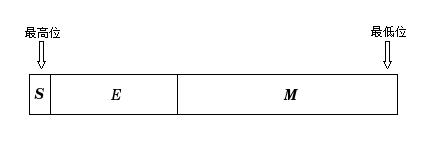
浮点数的计算结果为：

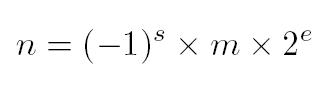
n,s,e,m分别为N,S,E,M对应的实际数值,而N,S,E,M仅仅是一串二进制位。
 S(sign)表示N的符号位。对应值s满足：n>0时，s=0; n<0时，s=1。
E(exponent)表示N的指数位，位于S和M之间的若干位。对应值e值也可正可负。
 M(mantissa)表示N的尾数位，恰好，它位于N末尾。M也叫有效数字位（sinificand）、系数位（coefficient）, 甚至被称作“小数”。

 

在IEEE-754标准下，浮点格式主要分为四种类行，即单精度格式、双精度格式、扩展单精度格式和扩展双精度格式。其中32位单精度格式与64位双精度格式作为基础格式更为常用，扩展格式则有特殊目的，一般对用户透明。

 

精度(有效数字)主要看尾数位： 
float的尾数位是23bit，对应7~8位十进制数，所以有效数字有的编译器是7位，也有的是8位
23位“尾数”位
【2^23=8388608，一共7位，这意味着最多能有7位有效数字，但是能绝对能保证的为6位，也即float的精度为6~7位。】

对于小于8388608的数字有效数字为7位，对于大于8388608的数字的有效数字为6位

float fff=1.2345678912345;
qDebug()<<QString("%1").arg(fff, 0, 'g', 14);

结果为：1.2345678806305

float fff=83886081234567;
qDebug()<<QString("%1").arg(fff, 0, 'g', 14);

结果为：83886080000000

float fff=83886081;
qDebug()<<QString("%1").arg(fff, 0, 'g', 14);

结果为：83886080

float fff=99999999;
qDebug()<<QString("%1").arg(fff, 0, 'g', 14);

结果为：100000000